PROFMAT e SIEM 2025 - Évora
Alteração de salas
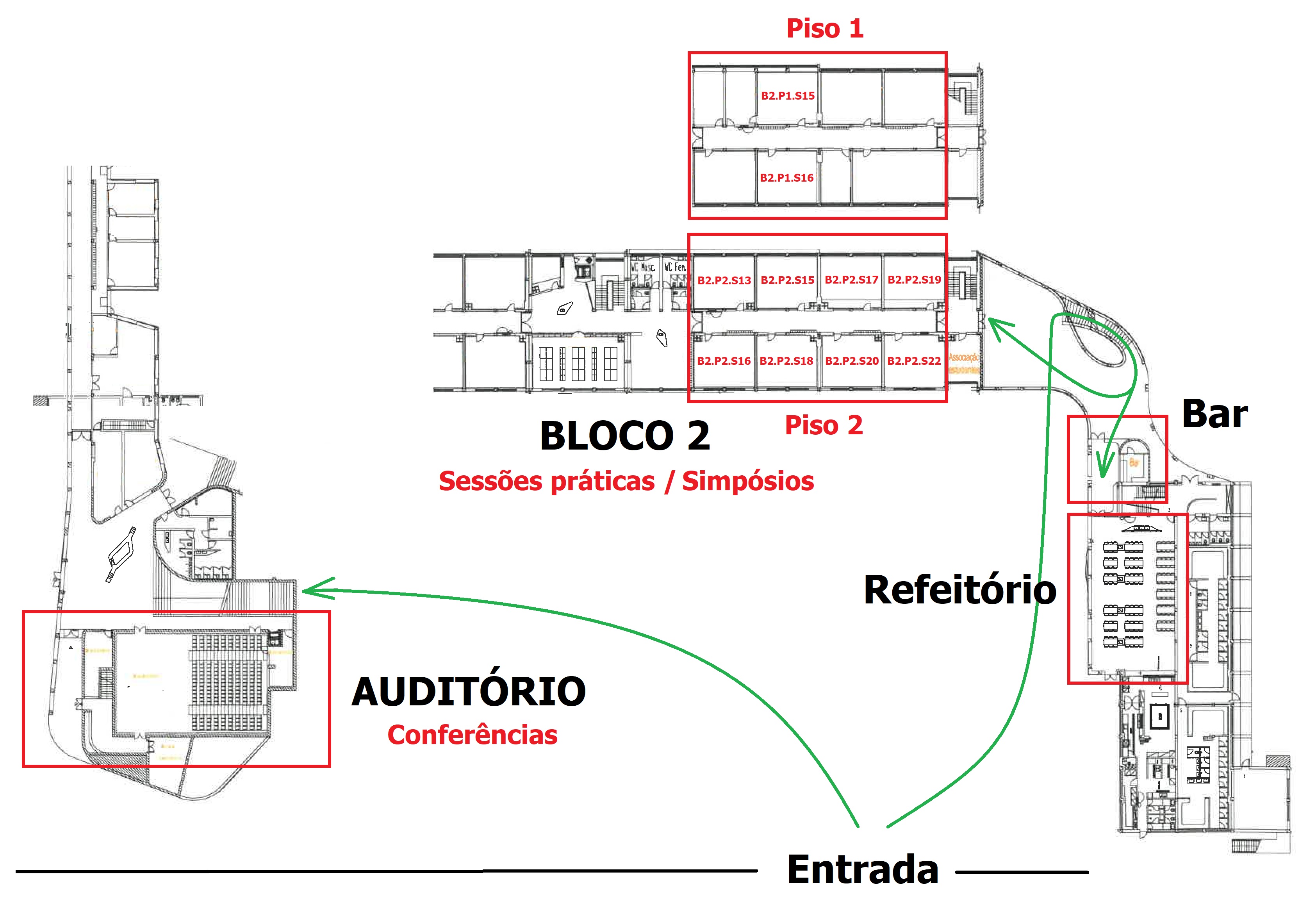
Dia 15 SP 09 passa para a sala 104
SP 01 passa para a sala 104
Dia 16 SC 07 passa para a sala 106
XL ProfMat e XXXV SIEM
O ProfMat volta a Évora!
1995, 2005, 2015, 2025. …
O ProfMat, Encontro Nacional de Professores de Matemática, anualmente organizado pela APM, volta a Évora!
Aqui tivemos oportunidade de comemorar os dez anos de ProfMat, em 1995, os vinte em 2005 e os 30 em 2015. Aqui esperamos voltar a reencontrar-nos, todos, para comemorar os 40 anos de Encontros.
40 anos é muito tempo! Muitos dias, muitas horas… de trabalho, de entusiasmos, de esmorecimentos, de exaltações, de lutas, de avanços e recuos, de novas paixões.
É muito tempo de busca por uma escola culturalmente significativa, onde se viva e construa conhecimento culturalmente validado – como referia Rui Trindade na conferência de abertura do Profmat de 2023.
Este ano não vai haver um tema central do Encontro, mas certamente estarão sempre presentes e subjacentes os novos programas – as novas Aprendizagens Essenciais – das disciplinas de Matemática, e onde olhares e perspetivas diferentes são sempre desejáveis e bem-vindas, numa postura de autoquestionamento contínuo que se traduza num desenvolvimento profissional, pessoal e coletivo, também contínuo.
E que melhor local para nos acolher desta vez?
Dele, escrevia Vergílio Ferreira, no seu romance Aparição: Às vezes (…) ficava na aula (…) olhando a planície, dourada de um sol trémulo ou varrida de grandes
vagas de chuva. (…) Outras vezes (…) passeava pelos claustros ou no jardim. De tarde a fila de arcadas batida de sol tinha uma luz interior, recortava-se em sombras nos azulejos da parede. (…) Dos telhados, pombos desciam, em linhas convergentes, para a taça da fonte.
Referimo-nos ao Colégio do Espírito Santo, edifício nobre da velha Universidade de Évora, que tantos de nós ajudou a formar!
Descobrir a Aula da Esfera, da Física, da Engenharia Militar, da Poesia Lírica… Procurar o Centro do Mundo e visitar a sala das Belas Artes que melhor enquadramento poderíamos ter para preencher os intervalos das sessões ou os momentos de pausa dos nossos trabalhos?
40 anos são muitos anos! Alguns de nós partiram…
Mas é tempo de reencher o peito de ar! De nos encontrarmos de novo!
Sempre!
Porque sempre perseguimos o entusiasmo dos principiantes, porque sempre queremos criar aqui lhe deixamos, pois, o convite para este campus anual de
reflexão, partilha e encontros em que o Profmat sempre se constitui.
Em Évora e na sua Universidade!
Joaquim Félix
DISPENSA ESPECIAL DE SERVIÇO
Foi concedida dispensa especial de serviço nos dias 14, 15 e 16 de julho aos professores dos Grupos de Recrutamento 110, 230 e 500 para poderem participar no ProfMat 2025.
Évora
Clique sobre a imagem para pesquisar no mapa:
Vídeo de Apresentação do ProfMat 2025
Cartaz do ProfMat e do SIEM 2025
Para esta edição do ProfMat e do SIEM, a APM promoveu um concurso de cartazes no qual participaram 109 alunos dos três Agrupamentos de Escolas das Caldas da Rainha.
Cartaz vencedor
Seguidamente, apresentam-se os premiados em cada categoria, por decisão do Júri do Concurso:
Premiados na categoria "A.E. Dom João II":
| 1.º Lugar | 2.º Lugar | 3.º Lugar |
Premiados na categoria "A.E. Rafael Bordalo Pinheiro":
| 1.º Lugar | 2.º Lugar | 3.º Lugar |
Parabéns a todos os participantes!
Recordamos os 64 candidatos a "Cartaz ProfMat e SIEM 2024":
CARTAZES DO A.E. Ds.
Comissão organizadora
Ana Paula Canavarro
António Borralho
António Cardoso
Beatriz David
Carla Mesquita
Constança Sofia Barreira
Elsa Barbosa
Joana Latas
Joaquim Pinto
Manuel João Marques
Maria Beatriz Martins
Paulo Correia
Pedro Macias Marques
Sofia Delgadinho
Sofia Silva
Teresa Correia Gonçalves
Locais do ProfMat 2025
O ProfMat 2024 decorre nas Universidade de Évora, mais especificamente em dois locais:
CENTRO CULTURAL E CONGRESSOS DE CALDAS DA RAINHA (CCC)
Mapa:
Rua Dr. Leonel Sotto Mayor 23D, 2500-227 Caldas da Rainha
Tlf: 262 094 081
Email: bilheteira@ccc.com.pt
URL: https://ccc.com.pt
 |
 |
ESCOLA SECUNDÁRIA RAFAEL BORDALO PINHEIRO (ESRBP)
Mapa:
Rua Almirante Gago Coutinho 1, 2500-000 Caldas da Rainha
Tlf: 262 870 070
Email: esrbp@esrbp.pt
URL: https://aerbp.pt
 |
 |
MAPA DA ZONA ENVOLVENTE

MAPA DA E. S. RAFAEL BORDALO PINHEIRO
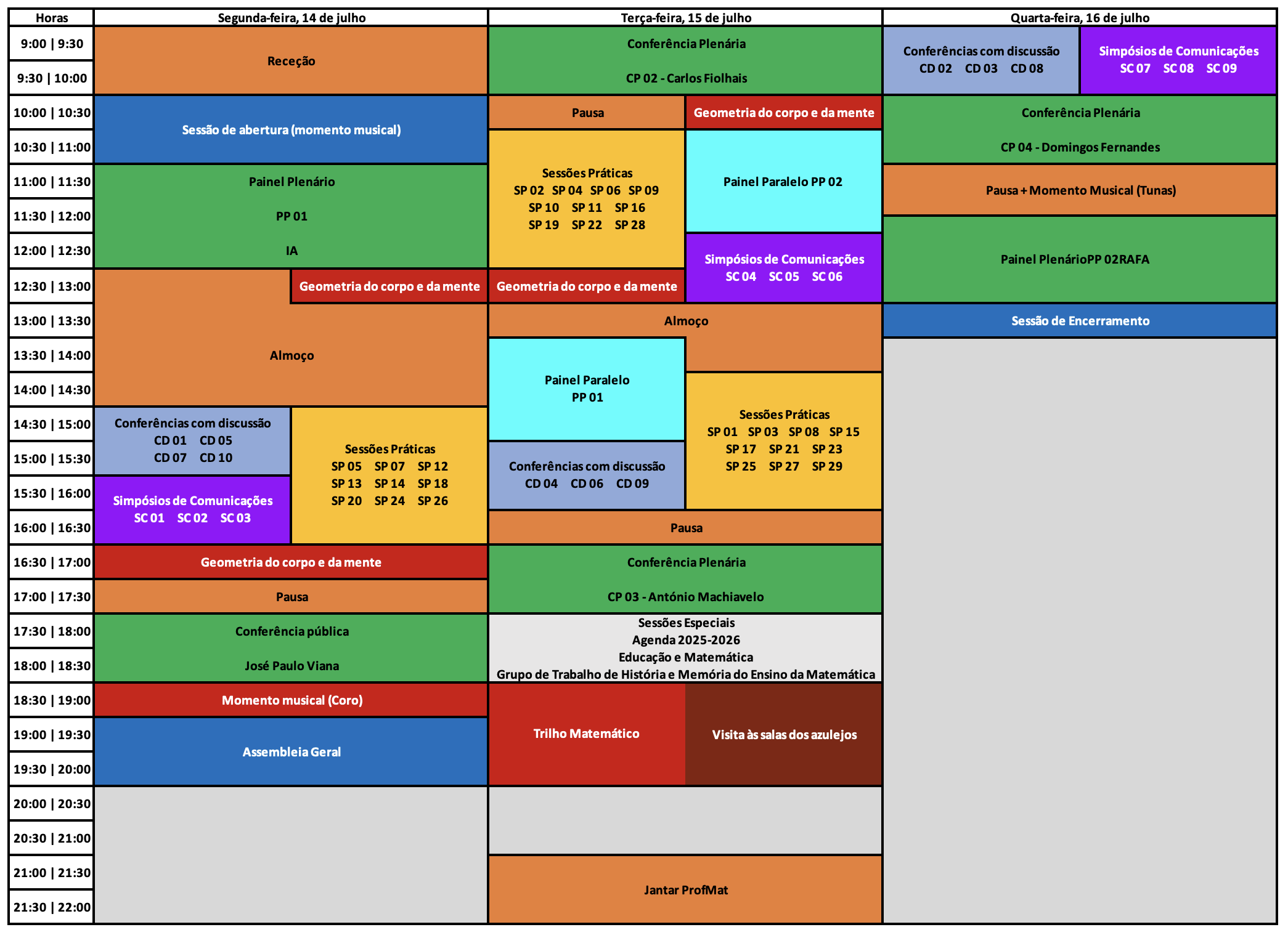
Programa ProfMat 2025
Almoços | Jantar do ProfMat
Almoços - 14, 15 e 16 de julho
Durante o ProfMat 2025, pode reservar as seguintes opções para almoçar:
| Preço | Pratos | 14 julho | 15 julho | 16 julho | 17 julho | |
|
Cozinha do Cardeal (máx. 60 lugares) |
18 euros |
Peixe Carne Vegetariano |
||||
|
Colégio Luís de Verney (máx. 190 lugares) |
10 euros |
Peixe Carne Vegetariano |
||||
|
Colégio Pedro da Fonseca (máx. 60 lugares) |
10 euros |
Peixe Carne Vegetariano |
Cada almoço na "Cozinha do Cardeal" tem um custo de 18 euros, e no "Colégio Luís de Verney" ou no "Colégio Pedro da Fonseca" estes dois um custo de 10 euros, pagos no ato de inscrição.
Jantar do ProfMat 2025 - Terça-feira 15 de julho
Mar De Ar Muralhas
URL: https://mardearhotels.com/
 |
 |
EMENTA
Sopa: Creme de ervilhas com ovo cozido
Peixe: Cação de coentrada, batata a murro com azeite, alho e orégãos
Carne: Lombinho de porco com massa de pimentão e migas de espargos
Seleção de frios & saladas, sobremesas e bebidas
Preço por pessoa: 30,00 €
Alojamentos com protocolo
Nas Caldas da Rainha, bem como nas proximidades, encontram-se várias opções de alojamento. Seguidamente, apresentam-se algumas destas opções. As tarifas indicadas foram comunicadas à Comissão Organizadora do ProfMat pelos respetivos alojamentos.
HOTEL CRISTAL CALDAS ***
O Hotel Cristal Caldas está localizado bem no centro da cidade termal das Caldas da Rainha (a 650 metros do Centro Cultural e de Congressos) e a apenas 7 km da Praia Foz de Arelho. O hotel possui 113 quartos e uma piscina exterior.
Localização - R. António Sérgio 31, 2500-130 Caldas da Rainha
Telefone - 262 840 260
Email - booking3@hoteiscristal.pt
Website - https://www.hoteiscristal.pt/cristal-caldas/
Tarifas de alojamento, por noite, por quarto:
Single - 66,00 € - 55,00 €
Duplo - 73,00 € - 65,00 €
Com pequeno-almoço buffet incluído
Nota: As reservas deverão ser efetuadas por email ou telefone e deverão mencionar que são participantes no ProfMat.
HOTEL
Onto.
Submissão de Comunicações e Sessões Práticas
Os participantes no ProfMat podem submeter propostas de comunicações e sessões práticas.
As propostas devem seguir as indicações dos respetivos modelos e serem enviadas até 31 de maio, através dos formulários abaixo.
A notificação acerca da aceitação da proposta será enviada até 12 de junho.
COMUNICAÇÃO EM SIMPÓSIO
As comunicações para os simpósios são propostas e dinamizadas por participantes no encontro, fundamentalmente sobre temas e abordagens de ensino e materiais didáticos. Cada comunicação tem a duração de 15 minutos e está integrada num simpósio de comunicações, reservando-se, no final do respetivo simpósio, 15 minutos para discussão coletiva.
Modelo para submissão de Comunicação
| Submissão de Comunicação |
SESSÃO PRÁTICA
As sessões práticas são propostas e dinamizadas por participantes no encontro, fundamentalmente sobre temas e abordagens de ensino e materiais didáticos. Cada sessão prática tem a duração de 120 minutos.
Modelo para submissão de Sessão Prática
| Submissão de Sessão Prática |
Modelo de PowerPoint
Se vai apresentar alguma comunicação ou sessão prática e pretende utilizar um modelo comum, próprio deste ProfMat, descarregue-o aqui:
Acreditação
FORMAÇÃO
O “40.º Encontro Nacional de Professores de Matemática — ProfMat 2025” é um curso de formação de 18 horas acreditado pelo CCPFC para os grupos 110, 230 e 500 (CCPFC/ACC-135536/25) na dimensão científica e pedagógica.
Os docentes que tiveram assiduidade em pelo menos, dois terços (12 horas) do número total de horas da formação (18 horas) e receberam e-mail do Centro de Formação, para obter certificação, devem:
- Enviar, para o endereço de correio eletrónico do CFAPM (centroformacao@apm.pt) o relatório de reflexão crítica individual até dia 31/07/2025. O envio do relatório até à data indicada é da exclusiva responsabilidade do formando, não sendo aceites relatórios entregues depois de 31/07/2025. No Centro de. Formação respondemos a todos os e-mails. Caso não seja confirmada a receção do seu relatório, volte a contactar o Centro de Formação..
- Para a realização do relatório de reflexão crítica individual, utilizar o documento enviado pelo Centro de Formação APM e disponível também no site do encontro no menu ProfMat 2025, submenu Acreditação: https://www.apm.pt/profmat2025
- Preencher, até ao dia 31/07/2025 o questionário de avaliação disponível no link: https://forms.gle/286qndeCrYjmoYJi9.
- Contactar o CFAPM (centroformacao@apm.pt) para qualquer questão relacionada com o processo de acreditação.
AVALIAÇÃO DOS FORMANDOS
A avaliação é individual e traduz-se numa classificação final quantitativa, na escala de 1 a 10, expressa através do referencial de menções qualitativas previsto no n.º 2 do artigo 46.º do ECD aprovado pelo Decreto-Lei n.º 15/2007, de acordo com as seguintes ponderações:
Assiduidade – 40%
Relatório de reflexão crítica individual – 60%
ASSIDUIDADE
A assiduidade é comprovada através da assinatura de folha de registo de presença. Os formandos que não participem em pelo menos dois terços (12 horas) do número total de horas de formação (18 horas) não poderão obter aprovação. A assinatura das folhas de registo de presença, é da responsabilidade de cada formando.
RELATÓRIO DE REFLEXÃO CRÍTICA INDIVIDUAL
O relatório de reflexão crítica individual incidirá sobre a globalidade da temática do encontro, numa perspetiva global, integradora e sistemática, sendo liminarmente excluídos trabalhos que não respeitem esta condição ou não se enquadrem nas regras definidas:
"Este trabalho individual deve contemplar uma reflexão sobre as temáticas abordadas ao longo do Encontro e que constituíram o seu percurso formativo, realçando o contributo deste percurso para a sua prática letiva e desenvolvimento profissional”.
A avaliação do relatório de reflexão crítica individual será realizada de acordo com um conjunto de descritores disponíveis em
https://www.apm.pt/profmat2025 .
Nota: Os relatórios de reflexão são um elemento de avaliação individual e original. Caso se detete que o relatório foi realizado com Inteligência Artificial, este será anulado, não sendo permitido ao formando o envio de nova versão.
O relatório terá de ser redigido em documento digital (sugerimos o envio do trabalho em formato pdf) e gravado com o seguinte nome: (Nome_do_docente_grupo disciplinar)_ProfMat2025.
- Número mínimo de páginas: 1
- Número máximo de páginas: 3
- Margens: superior 2,5 cm, inferior 2,5 cm, lateral esquerda 3 cm, lateral direita 3 cm
- Fonte: Arial, tamanho 12, espaçamento 1,15
A avaliação final terá uma menção qualitativa (Insuficiente, Regular, Bom, Muito Bom e Excelente) e o valor final da classificação quantitativa, numa escala de 1 a 10. A acreditação da formação depende da obtenção da classificação mínima de cinco valores, na escala de 1 a 10.
CERTIFICAÇÃO DE FORMAÇÃO ACREDITADA
Para os formandos que cumpram todas as formalidades da formação acreditada, frequentem, pelo menos, dois terços do número total de horas do curso de formação e sejam aprovados, será emitido um Certificado de Formação.
Os certificados referentes à formação serão enviados, via e-mail, pelo Centro de Formação para cada um dos formandos aprovados a partir de outubro de 2025.
Os certificados de participação no encontro, são da responsabilidade da Comissão Organizadora.
Contactos
profmat2025@apm.pt
ProfMat 2025 - Associação de Professores de Matemática
Rua Dr. João Couto, n.º 27-A
1500-236 Lisboa
Tel.: +351 21 716 36 90 / 21 711 03 77
 |
 |
 |
 |
Materiais — ProfMat 2024
Os materiais que forem cedidos pelos conferencistas serão disponibilizados aqui, logo que nos forem enviado e/ou depois da realização do ProfMat.
Conferências Plenárias (1h)
As conferências plenárias são realizadas por pessoas convidadas pela organização e com reconhecida experiência na área em que vão intervir. Incidem sobre temas de interesse geral e realizam-se em espaços do programa de forma a que todos os participantes tenham possibilidades de assistir.
CP 01 - O desafio dos paradoxos no dia-a-dia e na MatemáticaJosé Paulo Viana, APM Segunda-feira, 14 de julho, 17h30m - 18h30m (Aberto ao público) Auditório da Universidade Moderador: Elsa Isabelinho Barbosa Resumo Os paradoxos têm tido sempre um papel curioso ao longo da história. Nas situações da vida real obrigam a pensar mais profundamente no que acontece, na matemática levam a reformular conceitos e a abrir novos campos. Nota biográfica
José Paulo Viana – Professor de Matemática aposentado do ensino secundário. Entusiasta das matemáticas recreativas e da Magia Matemática. Autor, durante mais de 28 anos, da secção semanal “Desafios” no jornal Público. Divulgador de Matemática através de conferências e sessões públicas. Em 2014 recebeu o Prémio Ciência Viva nos Media. Autor de manuais escolares e de livros de divulgação matemática e de matemáticas recreativas. Dinamizador de cursos de formação de professores nas áreas de probabilidades, de modelação, de resolução de problemas e de utilização das tecnologias no ensino.
|
CP 02 - O triunfo da Física QuânticaCarlos Fiolhais, Universidade de Coimbra Terça feira, 15 de julho, 9h00m - 10h00m Auditório da Universidade Moderador: Joaquim Pinto Resumo A ONU declarou que 2025 seria o Ano Internacional da Ciência e Tecnologia Quânticas, assinalando a passagem dos cem anos do seu estabelecimento na dua forma actual, com os trabalhos de Werner Heisenberg, Erwin Schrödinger e de Max Born. Após uma introdução histórica, em que falarei dos inícios da teoria quântica com Max Planck, Albert Einstein, Niels Bohr e Louis de Broglie, apresentarei uma breve descrição dos trabalhos de 2025 e anos subsequentes, enfatizando alguns dos seus aspectos matemáticos. Falarei de alguns problemas filosóficos da teoria quântica (probabilidades, incerteza, papel do observador, etc,.) e de algumas das suas aplicações (transístor, laser, ressonância magnética, etc.). Concluirei com uma poderosa aplicação que está no horizonte - a computação quântica – que promete revolucionar o mundo da informática. A teoria quântica triunfou, mas o seu triunfo poderá ainda ser maior. Nota biográfica
Carlos Fiolhais – Nascido em Lisboa (1956), doutorou-se em Física Teórica na Universidade Goethe, Frankfurt (1982). É professor emérito da Universidade de Coimbra (UC). É autor de 70 livros e de numerosos artigos, um dos com recorde português de citações. Fundou o Centro Computacional da UC onde montou o 1.º supercomputador nacional. Dirigiu a Biblioteca Geral da UC, onde criou repositórios digitais, e dirige a colecção Ciência Aberta da Gradiva. Ganhou vários prémios e distinções, entre as quais o Globo de Ouro da SIC em 2005. |
CP 03 - A Essência da MatemáticaAntónio Machiavelo, Departamento de Matemática da Faculdade de Ciências do Porto Terça-feira, 15 de julho, 16h30m - 17h30m Auditório da Universidade Moderador:Raúl Gonçalves Resumo "Para que serve?” é seguramente a pergunta mais frequente que é feita sobre a matemática, em especial pelos estudantes. Argumentar-se-á nesta sessão que, antes de tentar responder a esta questão, é necessário precisar o que é exatamente a matemática, questão que tem vindo a causar muita perplexidade a filósofos, e aos próprios matemáticos, desde a Grécia Antiga até aos dias de hoje. Nesta intervenção não iremos, nem de perto, nem de longe, ao fundo das questões e dos problemas filosóficos subjacentes, mas, através de exemplos extremamente concretos, pretendemos deixar claro alguns dos aspetos daquilo que achamos ser a essência da matemática, e de como esta é um instrumento fundamental para descobrir o lado invisível do universo. Iremos demonstrar que, de um certo ponto de vista, a matemática é verdadeiramente mágica! Nota biográfica
António Machiavelo – Matemático na Faculdade de Ciências da Universidade do Porto. Adora ensinar, adquirir e divulgar conhecimento, praticar malabarismo, aprender línguas e escabichar os bons livros. |
CP 04 - Para melhorar as Políticas e Práticas Educativas: Contributos do Conselho Nacional de EducaçãoDomingos Fernandes, Conselho Nacional de Educação, Centro de Investigação e Estudos em Sociologia — Instituto Universitário de Lisboa (Iscte) Quarta-feira, 16 de julho, 10h00m - 11h00m Auditório da Universidade Moderador: António Borralho Resumo O Conselho Nacional de Educação (CNE), órgão independente e de consulta da Assembleia da República e do Governo, através das suas publicações periódicas (Estado da Educação e DICA – Divulgar, Inovar, Colaborar, Aprender), assim como dos pareceres, recomendações e contributos diversos, materializa o acompanhamento e a avaliação que vai fazendo acerca das políticas e práticas educativas. Nesta conferência, apresentam-se e discutem-se algumas questões críticas que emergem das posições expressas pelo CNE no Estado da Educação 2023 e também das investigações e narrativas de projetos constantes no DICA 2024. Salientam-se, por um lado, questões relativas à estrutura do sistema educativo (e.g., Educação dos 0 aos 12 anos e Educação Secundária) e, por outro lado, questões relativas ao Currículo e à Inovação Pedagógica, à Formação de Professores, e à Equidade, Democratização e Qualidade da Educação. A partir das questões suscitadas, fazem-se considerações e produzem-se reflexões acerca de relações entre a investigação considerada necessária para fundamentar e melhorar as políticas e práticas educativas. Nota biográfica
Domingos Fernandes – Presidente do Conselho Nacional de Educação desde 9 de junho de 2022. Investigador no Centro de Investigação e Estudos de Sociologia (ISCTE). Os seus interesses de investigação decorrem das Relações entre Currículo, Pedagogia e Avaliação. Professor visitante em diversas universidades internacionais. Investigador principal de projetos financiados no âmbito de concursos públicos. O seu artigo mais recente intitula-se Conhecimento, discernimento e ação em avaliação pedagógica: O legado de Leonor Santos publicado em 2024 na revista Quadrante da APM. |
Painéis Plenários (1,5h)
Sessão especialmente organizada para promover uma discussão sobre um tema de atualidade, com vários intervenientes convidados para o efeito. É preparada e conduzida por um moderador convidado pela organização que solicita intervenções dos vários participantes do painel sobre o tema em discussão e em resposta a questões da assistência que em momento próprio é convidada a intervir.
PP 01 - Pensar com Máquinas - uma nova cognição partilhadaModerador: Jaime Carvalho e Silva, Universidade de Coimbra Intervenientes: Nelson Zagalo, Universidade de Aveiro Segunda-feira, 14 de julho, 11h00m - 12h30m Auditório da Universidade Resumo O uso da Inteligência Artificial no Ensino em geral e no ensino da Matemática em particular é um tema que suscita cada vez maior debate e até alguma controvérsia. Desde aqueles que não vêem nenhuma vantagem no uso de tais novas ferramentas (concretamente Grandes Modelos de Linguagem) até aos que entendem que os professores irão ser substituídos dentro de uns 10 anos (como prevê Bill Gates), existe uma grande panóplia de opiniões. Como poderão ser usados os Grandes Modelos de Linguagem como ChatGPT ou o Gemini na Educação? E no Ensino da Matemática? O caminho para o uso da IA no ensino seguindo pela Khan Academy, pelo Goegbra e pela Wolfram/Mathematica é promissor? Os erros/alucinações irão causar perturbações ou mesmo uma crise de confiança? Poderão os professores planear as suas aulas com o ChatGPT ou o Gemini? E deverão proibir os alunos de os usar? Como os algoritmos da IA podem aprimorar a avaliação automatizada na Matemática, proporcionando feedback rápido e preciso? Em que medida essa abordagem pode contribuir para a eficiência na avaliação, libertando tempo aos professores para se concentrarem em interações mais significativas com os alunos? De que forma a IA pode contribuir para o desenvolvimento de competências como o pensamento crítico, a colaboração a criatividade e a agência dos alunos?
Jaime Carvalho e Silva - Professor Associado do Departamento de Matemática da FCT da Universidade de Coimbra. Membro do Centro de Investigação Matemática CMUC (UC). Responsável por disciplinas do 1º ano de cursos de Engenharia/Ciências/Gestão e do Mestrado em Ensino de Matemática da FCTUC. Docente do Programa de Doutoramento em História das Ciências e Educação Científica. Coordenador do Mestrado em Ensino de Matemática para o 3º Ciclo do Ensino Básico e Ensino Secundário da FCTUC. Autor de textos para o Ensino Básico, Secundário e Superior. Premiado duas vezes com o prémio Sebastião e Silva da SPM para manuais escolares. Co-autor dos programas de Matemática para o Ensino Secundário de 1997, 2001 e 2023, incluindo Matemática A e B, MACS e Matemática dos Cursos Profissionais e Artísticos. Coordenador do Grupo de Trabalho de Matemática nomeado pelo ME (2018-2020) e que publicou um documento com “Recomendações". Membro da Comissão Executiva e Secretário-Geral do ICMI-Comissão Internacional para a Instrução Matemática (2008-2010 e 2010-2012 respetivamente). Participou na elaboração de vários estudos do ICMI, nomeadamente os relativos ao uso da História da Matemática no Ensino, ao Ensino Superior de Matemática, às Inovações Curriculares e ao Ensino da Geometria.
Nelson Zagalo - Professor Catedrático na Universidade de Aveiro e Coordenador Científico do DigiMedia - Centro de Investigação de Media Digitais e Interacção. Fundou a Sociedade Portuguesa para as Ciências dos Videojogos e o Journal of Digital Media & Interaction. Coordenou e/ou participou em mais de 20 projetos científicos com financiamento
Irene Pimenta Rodrigues - Professora Associada do Departamento de Informática da Universidade de Évora e Investigadora integrada no Pólo do NOVA LINCS de Évora. Concluiu o doutoramento em Informática pela Universidade Nova de Lisboa em 1995. Os tópicos de investigação incluem Processamento de Língua Natural, Representação do Conhecimento e Raciocínio, Ontologias da Web Semântica e Sistemas de Diálogo.
João Couvaneiro - Professor na Egas Moniz – School of Health & Science, onde dirige o Departamento de Inovação Pedagógica; é Conselheiro do Conselho Nacional de Educação, integrando as comissões de inovação pedagógica e ensino superior; Conselheiro do Conselho Nacional de Inovação Pedagógica no Ensino Superior; Expert Delegate no Teaching with Al Thematic Working Group do Digital Education Council; membro da Comissão Executiva do SAPIEN - South and Atlantic Pedagogical Innovation & Excellence Network; faz parte do Conselho Pedagógico do Almada International School; Apple Professional Learning Specialist. Desempenhou funções de assessoria especializada na área da educação e formação de jovens e adultos, no Gabinete do Secretário de Estado da Educação. Foi Professor da Faculdade de Letras da Universidade de Lisboa. Foi Professor Coordenador e Diretor da Escola Superior de Educação Jean Piaget de Almada. Lecionou em diversos estabelecimentos de ensino básico e secundário. Com o apoio do Institute of Art, Design and Technology (Irlanda), desenvolveu em Moçambique o projeto School in a Box. Tem apoiado processos de inovação educacional e de integração das tecnologias em contextos educativos. Reconhecido como Apple Distinguished Educator, foi também finalista da edição mundial do Global Teacher Prize. Integrou a Direção da Agência Nacional para a Qualificação e Ensino Profissional. Foi membro do Conselho de Administração do Madan Parque. É membro do Conselho Estratégico Instituto de Nanoestruturas, Nanomodelação e Nanofabricação (i3N), do Conselho Consultivo da Associação Portuguesa de Educação e Formação de Adultos, da Academia Olímpica de Portugal, Secretário da Assembleia Geral do Instituto de Apoio à Criança, e Presidente do Conselho Científico da Associação Portuguesa para a Inovação e Empreendedorismo Social e Digital. Integrou o Conselho Geral de diversas escolas agrupamentos de escolas. Foi eleito vereador da Câmara Municipal de Almada nas eleições autárquicas de 2017-2021, onde assumiu a vice-presidência e diversos pelouros, entre eles o da educação. No mandato de 2021-2025 é deputado municipal e preside à Comissão de Educação, Desporto, Juventude e Cultura da Assembleia Municipal de Almada.
Pedro Nogueira - Professor da disciplina de Ciência de Dados Espaciais Aplicada no Mestrado em Geociências da Universidade de Évora, onde são abordadas metodologias de análise automática de dados geológicos. Esta atividade tem sido integrada em projetos de investigação e de prestação de serviços. participou em vários projetos internacionais nas áreas das geociências e apoio institucional. Trabalhou com entidades de países como Timor-Leste, Moçambique e República Dominicana, prestando apoio técnico e científico em áreas como cartografia geológica, gestão de dados espaciais e formação em geociências. Em Timor-Leste, colaborou na criação do Instituto de Petróleo e Geologia (IPG-TL) e contribuiu para o desenvolvimento do curso de Geologia e Petróleo na Universidade Nacional Timor Lorosae. Estas atividades incluíram também ações de capacitação técnica e apoio à gestão de recursos minerais. Nos últimos anos, tem desenvolvido trabalho na aplicação de métodos de Inteligência Artificial (IA) e Machine Learning (ML) a dados geoespaciais. Utiliza estas técnicas para análise e modelação de dados em projetos de prospeção mineral, deteção remota e geoestatística. |
PP 02 - Projeto RAFA: Relações entre Avaliação Formativa e as Aprendizagens na aula de matemáticaModerador: Marcelo Coppi, Universidade de Évora Intervenientes: António Borralho, Universidade de Évora Quarta-feira, 16 de julho, 11h30m - 13h00m Auditório da Universidade Resumo A investigação tem-nos mostrado que é frequente os processos de ensino e das aprendizagens dos alunos decorrerem de forma articulada na sala de aula, não havendo uma separação entre quando um acaba e o outro começa. Recorrentemente estes processos são analisados de forma conjunta e complementar. Mas, quando é para avaliar há um momento específico para tal, ou seja, é um processo algo independente dos processos de ensino e de aprendizagem – há uma quebra. Parou, que agora vamos avaliar! Porquê? Neste contexto, foi desenvolvido um modelo didático inovador que emergiu de um estudo empírico com foco na análise e articulação entre os processos de ensino, avaliação e aprendizagem numa sala de aula de matemática do 7.º ano de escolaridade, no âmbito de um projeto de investigação mais alargado. Os resultados da implementação do modelo evidenciam que as práticas letivas em estreito relacionamento com a implementação de tarefas incluindo propósitos de ensino, avaliação e aprendizagem, bem como com o currículo, são consistentes com o desenvolvimento da autorregulação das aprendizagens e da participação dos alunos, o que conduziu a uma melhoria nas suas aprendizagens.
Marcelo Coppi - Assistente Convidado na Universidade de Évora (Departamento de Pedagogia e Educação) e doutorando em Ciências da Educação. Como investigador no Centro de Investigação em Educação e Psicologia da Universidade de Évora, desenvolve projetos e publica nas áreas da avaliação pedagógica, literacia científica e formação de professores.
António Borralho - Doutor em Ciências da Educação (Educação Matemática) pela Universidade de Évora, mestre em Tecnologia Educativa pela Universidade de Salamanca (Espanha) e licenciado em Ensino de Matemática e Desenho pela Universidade de Évora. É Professor Associado da Universidade de Évora e membro integrado do Centro de Investigação em Educação e Psicologia. A educação matemática é o seu principal interesse de investigação, tendo as suas publicações incidido na didática e na avaliação das aprendizagens.
Elsa Barbosa - Doutora em Ciências da Educação (Educação Matemática), mestre em Educação Matemática e licenciada em Matemática (Ensino de) pela Universidade de Évora. Membro integrado no Centro de Investigação em Educação e Psicologia da mesma universidade. Professora de Matemática exercendo, atualmente, o cargo de subdiretora do AE Manuel Ferreira Patrício. Participa em redes de investigação associadas a universidades federais no Brasil. A educação matemática é o seu principal interesse de investigação.
Joana Latas - Doutora em História das Ciências e Educação Científica pela Universidade de Coimbra, mestre em Ciências da Educação – Supervisão Pedagógica e licenciada em Matemática e Ciências da Computação pela Universidade de Évora. É membro integrado do Centro de Investigação em Educação e Psicologia da Universidade de Évora e professora de Matemática. Tem investigação publicada na área da educação matemática, educação científica em contextos não formais e em avaliação pedagógica
Maria João Rocha - Terminou a licenciatura em Ensino Básico 1º ciclo, pela Universidade de Évora, no ano de 2002 e, desde então, desempenhou funções como docente titular de turma e como docente de apoio educativo, em diferentes agrupamentos do Alentejo e da região de Lisboa. Desde 2021, exerce funções como docente titular de turma, atualmente numa turma de 2º ano, na Escola Básica da Cruz da Picada, pertencente ao Agrupamento de Escolas Manuel Ferreira Patrício, em Évora. É também professora Cooperante no âmbito da parceria com a Universidade de Évora. |
Painéis Paralelos (1,5h)
Sessão especialmente organizada para promover uma discussão sobre um tema de atualidade, com vários intervenientes convidados para o efeito. É preparada e conduzida por um moderador convidado pela organização que solicita intervenções dos vários participantes do painel sobre o tema em discussão e em resposta a questões da assistência que em momento próprio é convidada a intervir.
P 01 - Aprendizagens Essenciais de Matemática no Secundário: Que desafios para os professores?Moderador: João Almiro, Escola Secundária de Tondela Intervenientes: Ana Paula Júlio, Agrupamento de Escolas de Alcácer do Sal Terça-feira, 15 de julho, 13h30m - 15h00m Anfiteatro 131 Resumo As alterações curriculares trazem sempre grandes desafios para os professores, tanto ao nível dos novos temas e tópicos, como ao nível das metodologias a utilizar em sala de aula, mas também no que respeita aos recursos, especialmente tecnológicos, muitas vezes indispensáveis para o ensino aprendizagem da matemática.
João Almiro - Licenciou-se em Matemática e obteve o grau de Mestre em Educação – Didáctica de Matemática na Faculdade de Ciências da Universidade de Lisboa. Foi professor de Matemática na Escola Secundária de Tondela, tendo estado envolvido em vários programas de formação tanto em Centros de Formação de Associação de Escolas, como em colaboração com o Ministério da Educação e a APM. Integrou os grupos de trabalho que redigiram as "Recomendações para a melhoria das aprendizagens dos alunos em Matemática" e as Aprendizagens Essenciais de Matemática para o Ensino Secundário.
Ana Paula Júlio - Licenciada em Ensino de Matemática pela Universidade de Évora, onde também concluiu o Curso de Especialização em Educação - Administração Escolar. É professora de Matemática do 3.º ciclo e do Ensino Secundário no Agrupamento de Escolas de Alcácer do Sal, desde 1999. Foi orientadora de estágio/prática pedagógica supervisionada pela Universidade de Évora e Supervisora no Processo de Classificação de Exames Nacionais do IAVE e é formadora acreditada pelo CCPFC nas áreas de Matemática e Administração Educacional.
Cristina Cruchinho - É professora na Escola Secundária, com 3.º ciclo Filipa de Vilhena e tem estado envolvida em projetos de formação de professores em colaboração com CFAE, a DGE, a APM e a FCUP. Integrou o grupo de trabalho que redigiu as Aprendizagens Essenciais de Matemática para o Ensino Secundário. É uma dos dez professores que lecionam, desde o ano letivo de 2023/2024, as turmas piloto de Matemática A.
José Carlos Pereira - Professor de Matemática, licenciado pela Faculdade de Ciências da Universidade de Lisboa com estágio profissional na Escola Secundária Seomara da Costa Primo. Dedica-se ao seu centro de explicações de Matemática desde então. É administrador do grupo de Facebook Recursos para Matemática, onde gere e fomenta a partilha e discussão de temas relacionados com a Matemática e a sua docência entre mais de 9000 membros. Coautor do livro de apoio escolar Preparar o Exame Matemática A, da Raiz Editora e do manual Matemática 360 da mesma editora. Colaborador do Clube de Matemática da Sociedade Portuguesa de Matemática, com a coluna «Se e só se».
Marília André do Rosário - É licenciada em Matemática pela Faculdade de Ciências da Universidade do Porto e Mestre em Supervisão Pedagógica em Ensino da Matemática pela Universidade do Minho. É docente do Agrupamento de Escolas Tomaz Pelayo. Foi Professora Acompanhante do Plano de Ação para a Matemática, Supervisora no Processo de classificação de Provas do IAVE, orientadora de estágio da FCUP e UM, formadora acreditada pelo CCPFC e é professora de uma turma piloto das AE para os Cursos Profissionais.
|
P 02 - Experiências de operacionalização das Aprendizagens Essenciais no Ensino Básico – partilha e discussãoModeradora: Lina Brunheira, Escola Superior de Educação de Lisboa Intervenientes: Joana Conceição, Agrupamento Escolas José Cardoso Pires Terça-feira, 15 de julho, 10h30m - 12h00m Anfiteatro 131 Resumo Em 2022/23 iniciou-se a operacionalização das AE em todo o território nacional, estando neste ano letivo, pela primeira vez, a abarcar todas as turmas do 1.º ao 9.º ano. Com esta experiência é já possível, e pertinente, fazer um primeiro balanço. Que estratégias de gestão de currículo têm sido adotadas e qual a sua eficácia? Quais os objetivos que se têm revelado mais desafiantes e como têm sido trabalhados? Que exemplos de experiências inovadoras merecem referência? Quais os contributos (e necessidades) que emergem para o desenvolvimento profissional?
Lina Brunheira - Licenciada em Ensino da Matemática e Mestre em Didática da Matemática pela Faculdade de Ciências da Universidade de Lisboa, Doutorada em Educação-Didática da Matemática pelo Instituto de Educação da Universidade de Lisboa. É coautora das Aprendizagens Essenciais de Matemática para o Ensino Básico e fez parte do grupo de trabalho que acompanhou as turmas que anteciparam a operacionalização do programa e conceberam o programa de formação contínua. Atualmente é professora adjunta na Escola Superior de Educação de Lisboa onde se dedica à formação inicial de educadores e professores de 1.º e 2.º CEB.
Joana Conceição - Licenciada em Ensino Básico-1.º Ciclo pela Escola Superior de Educação de Santarém e Mestre em Educação Matemática no Pré-escolar e 1.º e 2.º ciclos do ensino básico, pela Escola Superior de Educação de Lisboa. Em 2022, doutorou-se em Didática da Matemática, pelo Instituto de Educação da Universidade de Lisboa. Para além do trabalho no ensino básico, dedica-se à formação contínua de professores e mantém-se ligada à investigação, encontrando-se, atualmente, a colaborar no projeto IMAVIS, da ESELx, dedicado à interligação entre Matemática e Artes Visuais.
Nuno Valério - Licenciado em Ensino na variante de Matemática e Ciências da Natureza pela Escola Superior de Educação de Lisboa e Mestre em Educação (Didática da Matemática) pela Universidade de Lisboa. Realizou CFA em Formação de Professores no Instituto de Educação da Universidade de Lisboa. Dedica-se à formação contínua de professores tendo sido formador do Programa de Formação Contínua em Matemática para o 1º e 2º ciclo (2005-2011) e das Aprendizagens Essenciais de Matemática para o 2º ciclo do ensino básico. É autor de manuais escolares.
António Cardoso - Licenciado em Ensino de Matemática e possui o curso de especialização do Mestrado em Educação Matemática, pela Universidade de Évora. É professor do ensino básico (3.º ciclo) e secundário. Foi professor de uma turma de antecipação da generalização das novas Aprendizagens Essenciais (3.º ciclo). Desenvolve também atividade ao nível da formação de professores.
Renata Carvalho - Licenciada em Ensino na variante de Matemática e Ciências da Natureza pela Escola Superior de Educação (ESE) de Portalegre. Possui Mestrado em Educação na área de Didática da Matemática pela Faculdade de Ciências da ULisboa e Doutoramento na mesma área pelo Instituto de Educação da ULisboa. Tem colaborado em projetos e encontros nacionais e internacionais na área da Educação Matemática e na formação inicial e contínua de professores. Atualmente é Diretora do Centro de Formação da Associação de Professores de Matemática e professora adjunta convidada na ESE de Lisboa. |
Conferências com Discussão (1h)
As conferências com discussão são intervenções realizadas por pessoas convidadas pela organização para intervir em áreas ou temas considerados de interesse para os participantes. Incidem sobre assuntos diversificados e são seguidas de um espaço de discussão com os presentes, com um moderador convidado para o efeito.
|
CD 01 |
Avaliação por literacias (Resumo) Luís Pereira dos Santos, Instituto de Avaliação Educativa, I.P. Público: Geral |
Segunda-feira, 14 de julho 14h30 - 15h30 |
Sala 295 |
|
CD 02 |
Geometria, Aritmética e Álgebra — Como podemos beneficiar da sua unidade na sala de aula? (Resumo) Helmuth Malonek, UI & CIDMA/Universidade de Aveiro Público: Geral |
Quarta-feira, 16 de julho 9h00 - 10h00 |
Sala 298 |
|
CD 03 |
Laboratórios de Educação Digital (LED) (Resumo) Ana Paula Alves, DGE Público: Geral |
Quarta-feira, 16 de julho 9h00 - 10h00 |
Sala 295 |
|
CD 04 |
Einstein, Eddington e o Eclipse. Impressões de Viagem – Potenciar a Educação Científica através da arte visual e narrativas históricas (Resumo) Ana Simões, Faculdade de Ciências da Universidade de Lisboa Público: Secundário |
Terça-feira, 15 de julho 15h00 - 16h00 |
Anfiteatro 131 |
|
CD 05 |
AE do Ensino Profissional (Resumo) Mª Teresa Santos – Escola Profissional de Agricultura e Desenvolvimento Rural de Vagos. Público: Secundário |
Terça-feira, 15 de julho 15h00 - 16h00 |
Sala 298 |
|
CD 06 |
Estudo Autónomo atraves de Conteúdos educativos digitais (Resumo) Cláudia Torres, AE D. Dinis / Equipa de Projeto Estudo Autónomo Público: Secundário |
Terça-feira, 15 de julho 15h00 - 16h00 |
Sala 298 |
| CD 07 |
Uma viagem (muito breve!) pelas imagens mais importantes da história da ciência (e algumas implicações no ensino) (Resumo) Vítor Duarte Teodoro, Universidade Lusófona Público: Geral |
Segunda-feira, 14 de julho 14h30 - 15h30 |
Sala 115 |
| CD 08 |
Pensamento Computacional: Interlocuções com a Matemática e Perspecttivas Transdisciplinares (Resumo) Cláudio Zarate Sanavria, Instituto Federal de Mato Grosso do Sul (Brasil) Público: Secundário e Superior |
Quarta-feira, 16 de julho 9h00 - 10h00 |
Anfiteatro 131 |
| CD 09 |
E, ... entre pregos, martelos e microcomputadores, ... há 40 anos nasceu o PROFMAT (Resumo) José Manuel Matos, Universidade Nova de Lisboa Geral |
Terça-feira, 15 de julho 15h00 - 16h00 |
Sala 295 |
| CD 10 |
Capacidades matemáticas transversais: as novas brochuras para o Ensino Básico (Resumo) Ana Paula Canavarro, Universidade de Évora Ensino Básico |
Segunda-feira, 14 de julho 14h30 - 15h30 |
Anfiteatro 131 |
RESUMOS
CD 01 - Avaliação por literaciasLuís Pereira dos Santos, Instituto de Avaliação Educativa, I.P. Segunda-feira, 14 de julho, 14h30m - 15h30m Sala 295 Moderador: João Terroso Resumo As provas Monitorização das Aprendizagens (ModA) dos 4.º e 6.º anos de escolaridade têm como principais objetivos o estabelecimento de tendências de evolução das aprendizagens dos alunos ao longo dos anos, bem como a avaliação do «nível de literacia dos alunos», ou seja, a capacidade de os alunos mobilizarem conhecimentos e competências que lhes permitam resolver situações, em contextos diversificados, tomando como referência o Perfil dos Alunos à Saída da Escolaridade Obrigatória, nomeadamente as suas áreas de competências, e as Aprendizagens Essenciais.
Luís Pereira dos Santos – É Licenciado em Ensino da Física e Mestre em Didática das Ciências, pela Faculdade de Ciências da Universidade de Lisboa. Foi professor de Física e Química, Vice-Presidente do Conselho Executivo da Escola Secundária da Cidade Universitária. Foi Chefe de Divisão de Formação de Professores e Diretor de Serviços de Recursos Multimédia na DGIDC. Foi Presidente do Júri Nacional de Exames de 2011 a 2019. Exerce atualmente o cargo de Presidente do Conselho Diretivo do Instituto de Avaliação Educativa. Desde 2019, é o representantede Portugal no PISA Governing Board (OCDE) e na Assembleia Geral da IEA. |
CD 02 - História da MatemáticaHelmuth Malonek Quarta-feira, 16 de julho, 9h00m - 10h00m Sala 298 Moderadora: Manuel João Marques Resumo Se tentarmos transmitir a matemática como uma disciplina na sala de aula, na qual o conhecimento é reunido pedra por pedra para formar um edifício impressionante, então a unidade das suas subáreas desempenha um papel importante. Em quase todos os anos escolares, é possível traduzir relações geométricas em relações aritméticas (ou vice-versa) e obter novas percepções usando operações algébricas. Desta forma, a matemática, que muitas vezes é considerada apenas como uma disciplina difícil e abstrata, também pode ser concebida como uma emocionante viagem de descoberta para alunos curiosos.
Helmuth Malonek – Jubilou-se recentemente como professor de Matemática na Universidade de Aveiro, onde começou a trabalhar no Departamento de Matemática em 1992. Motivado por uma vasta experiência no ensino da história da matemática, desenvolve também investigação nesta área. |
CD 03 - Laboratórios de Educação Digital (LED)Ana Paula Alves, DGE Quarta-feira, 16 de julho, 9h00m - 10h00m Sala 295 Moderador: Sofia Delgadinho Resumo No âmbito da Transição Digital, a Direção-Geral da Educação (DGE) tem vindo a promover os Laboratórios de Educação Digital (LED), uma medida do Plano de Recuperação e Resiliência (PRR) que visa fomentar a inovação educativa e a melhoria das aprendizagens através da integração intencional das tecnologias digitais. Esta comunicação apresenta o enquadramento nacional do projeto LED e a sua articulação com o currículo, sublinhando a importância da criação e implementação de cenários de aprendizagem. Serão partilhados exemplos com potencial aplicação no ensino da Matemática. Destaca-se o papel da capacitação docente e das redes de colaboração na consolidação de práticas inovadoras e contextualizadas. Pretende-se, sobretudo, abrir espaço à reflexão sobre como os LED podem apoiar a aprendizagem da Matemática e contribuir para o desenvolvimento de competências essenciais nos alunos. Nota biográfica
Ana Paula Alves – Professora de Matemática. Doutorada em Ciências da Educação pela Universidade do Minho, com especialização em Tecnologia Educativa. Em mobilidade estatutária na Direção-Geral da Educação (DGE), colabora com o Centro de Competência TIC da Universidade do Minho. Integra atualmente a equipa do projeto “Laboratórios de Educação Digital” (LED), com responsabilidades na coordenação das estratégias de capacitação docente e de acompanhamento às escolas. |
CD 04 - Einstein, Eddington e o Eclipse. Impressões de Viagem – Potenciar a Educação Científica através da arte visual e narrativas históricasAna Simões, Faculdade de Ciências da Universidade de Lisboa Terça-feira, 15 de julho, 15h00m - 16h00m Anfiteatro 131 Moderador: Joana Latas Público: Geral Resumo Exploração da integração inovadora das artes no ensino das ciências, com base no livro Einstein, Eddington e o Eclipse: Impressões de Viagem. Este livro combina um ensaio de história da ciência com uma novela gráfica, criada em colaboração por Ana Simões, historiadora da ciência, e Ana Matilde Sousa, artista. Afastando-se das bandas desenhadas convencionais de divulgação científica, a secção da novela gráfica adota um estilo de “art comics”, com uma estética experimental e uma narrativa complexa, desafiando a ideia de que as bandas desenhadas simplificam em demasia os conceitos e eventos científicos.
Ana Simões – Professora Catedrática de História das Ciências na Faculdade de Ciências da Universidade de Lisboa. Foi fundadora e (co)coordenadora do Centro Interuniversitário de História das Ciências e daTecnologia entre 2007 e 2020. As suas publicações inserem-se nas áreas de história da química quântica e de história das ciências em Portugal. O seu trabalho sobre a apropriação do eclipse de 1919 pela comunidade astronómica de Lisboa foi o ponto de partida para o seu envolvimento nas comemorações do centenário do eclipse, em 2019. Entre várias atividades e publicações, comissariou a exposição E3. Einstein, Eddington e o Eclipse, e publicou o respectivo catálogo. É coordenadora do projecto financiado pela FCT “E3GLOBAL – Einstein, Eddington e o Eclipse. Uma história global do eclipse solar total de 1919.
Ana Matilde Sousa – É artista visual e investigadora de Lisboa. Em 2012, cofundou o selo português de Zines Clube do Inferno, começando a fazer BD sob o pseudónimo Hetamoé. Deste então, o seu trabalho tem sido apresentado por editoras de BD alternativa e outros espaços artísticos em Portugal e internacionalmente, incluindo Chili Com Carne, Kunstehalle Lissabon, Kuš!, Ediciones Valientes, Éditions Trip, Anthropocene Curriculum, Silent Army e Kuti. É doutorada em Pintura pela Faculdade de Belas Artes da Universidade de Lisboa, onde trabalha atualmente como Investigadora FCT Junior e professora na Licenciatura em Pintura.
|
CD 05 - AE do Ensino ProfissionalMª Teresa Santos, Escola Profissional de Agricultura e Desenvolvimento Rural de Vagos Segunda-feira, 14 de julho, 14h30m - 15h30m Sala 298 Moderadora: Nadia Ferreira Público: Secundário Resumo Nesta conferência pretende-se dar uma visão aprofundada sobre a implementação das Aprendizagens Essenciais em Matemática para o Ensino Secundário (Matemática B e Matemática do Ensino Profissional), homologadas em janeiro de 2023, através da perspectiva de duas das suas coautoras e simultaneamente envolvidas nas turma-piloto. Conscientes da necessidade de esclarecer e refletir em alguns tópicos das Aprendizagens Essenciais em Matemática para o Ensino Secundário, procurar-se-á destacar o que de mais significativo e novo existe nestes documentos curriculares, assim como partilhar e discutir o trabalho desenvolvido no âmbito das turmas piloto. Partindo das orientações curriculares expressas nas Aprendizagens Essenciais de Matemática para o Ensino Secundário e das suas finalidades, analisaremos algumas das tarefas implementadas, e que se encontram nas coletâneas publicadas na página da DGE e partilharemos as experiências vividas em sala de aula. Além disso, apresentaremos possíveis caminhos a seguir e desafios que podem surgir! Notas biográficas
Mª. Teresa Santos – Licenciada em Ensino da Matemática pela Universidade de Aveiro. Concluiu o primeiro ano do Mestrado em Ensino da Matemática, na FCUL e o primeiro ano do Doutoramento em História das Ciências e Educação Científica, na Universidade de Coimbra. É professora na Escola Profissional de Agricultura e Desenvolvimento Rural de Vagos. É coautora das novas Aprendizagens Essenciais de Matemática para o Ensino Secundário e Profissional.
Nélida Filipe – Licenciada em Ensino da Matemática, pela FCUC, mestre em Educação Matemática, pela UE e doutora em Educação-Didática da Matemática Instituto de Educação da UL. É professora no Agrupamento de Escolas Dra. Laura Ayres e professora adjunta convidada na ESEC da UALG. É coautora das novas Aprendizagens Essenciais de Matemática para o Ensino Secundário e Profissional, sendo igualmente coautora de manuais escolares. É Membro da equipa do núcleo do Algarve-APM.
|
CD 06 - Estudo Autónomo atraves de Conteúdos educativos digitaisCláudia Torres, AE D. Dinis / Equipa de Projeto Estudo Autónomo Terça-feira, 15 de julho, 15h00m - 16h00m Sala 298 Moderador: Hélder Martins Público: Secundário Resumo A literatura científica, tanto nacional como internacional, converge em destacar a relevância de promover o estudo autónomo nos alunos. Nos últimos anos, diversos estudos têm sublinhado que desenvolver competências de autorregulação desde cedo é crucial para o sucesso escolar e pessoal dos alunos. Ao aprender a gerir o próprio tempo, a pesquisar informação e a avaliar a própria aprendizagem, os alunos tornam-se mais confiantes e motivados para enfrentar os desafios do mundo em constante transformação.
Cláudia Torres – Professora de Matemática, doutora em Educação na área de especialização em Didática da Matemática (2014) com uma tese subordinada ao tema, A gestão do currículo no contexto de um grupo de professores de Matemática. A tese de mestrado é subordinada ao tema, A Avaliação como Regulação do Processo de Ensino-Aprendizagem da Matemática: Um Estudo com Alunos do 3.º Ciclo do Ensino Básico. Foi docente convidada no mestrado em Educação e mestrado em Ensino do Instituto de Educação da UL. Fez parte de equipas de projetos nacionais e internacionais. Presentemente, é coordenadora da Equipa de projeto Estudo Autónomo do MECI. |
CD 07 - Uma viagem (muito breve!) pelas imagens mais importantes da história da ciência (e algumas implicações no ensino)Vítor Duarte Teodoro, Universidade Lusófona Segunda-feira, 14 de julho, 14h30m - 15h30m Sala 115 Moderador: Pedro Macias Marques Público: Geral Resumo Esta conferência convida professores de matemática a explorar como imagens icónicas da história da ciência podem transformar o ensino e a aprendizagem. Serão revisitadas três representações visuais que revolucionaram o entendimento científico: o esboço de Darwin, que sugere a ancestralidade comum de todos os seres vivos; o esquema de Newton, que unifica os movimentos terrestre e celestial; e o gráfico de Hubble, que revela a expansão do universo. Cada imagem será contextualizada na sua época, destacando o seu impacto científico e as possibilidades pedagógicas que oferece na atualidade. Será discutido como estas representações condensam ideias complexas de forma intuitiva, despertando curiosidade e promovendo a interdisciplinaridade. No final, os participantes refletirão sobre estratégias práticas para integrar estas imagens e narrativas históricas nas suas aulas, tornando o ensino mais atrativo, interdisciplinar e significativo. Nota biográfica
Vítor Duarte Teodoro – Especialista em educação em ciências, com vasta experiência no ensino da Física, Matemática e Ciências da Computação, bem como na formação de professores. Doutorado em Educação pela Universidade Nova de Lisboa, coordenou programas de formação, investigou modelação matemática e tecnologia educativa. Autor de software educativo e manuais escolares, publicou em Portugal, nos EUA e noutros países. Foi consultor em reformas educativas, laboratórios escolares e recursos digitais, colaborando com instituições nacionais e internacionais, e integrou redes profissionais na Europa e América Latina. |
CD 08 - Pensamento Computacional: Interlocuções com a Matemática e Perspectivas TransdisciplinaresCláudio Sanavria, Instituto Federal de Mato Grosso do Sul (Brasil) Quarta-feira, 16 de julho, 9h00m - 10h00m Anfiteatro 131 Moderador: Joaquim Pinto Público: Geral Resumo Esta conferência convida os participantes a refletir sobre o pensamento computacional como prática educativa para os processos de ensino e aprendizagem da matemática, no contexto do ensino básico e secundário, vislumbrando perspectivas que apontem possibilidades de interlocuções com as demais áreas do conhecimento. O pensamento computacional é um conjunto de habilidades e práticas fundamentais da ciência da computação e envolve a resolução de problemas por meio de abstração, decomposição, reconhecimento de padrões e algoritmos. Ele é visto como uma competência importante para o desenvolvimento de habilidades de aprendizagem ao longo da vida, para a expressão pessoal e criatividade e para a formação de cidadãos críticos e conscientes. Nesse contexto, além de aspectos conceituais, serão discutidas questões relacionadas à estruturação docurrículo e levantamentos de experiências já realizadas no âmbito da sala de aula. Nota biográfica
Claudio Zarate Sanavria – Doutor em Educação pela Universidade Estadual Paulista “Júlio de Mesquita Filho” (Unesp), Brasil. Realiza pós-doutoramento em Informática na Educação na Universidade Federal do Rio Grande do Sul, Brasil, e em Educação e Psicologia na Universidade de Aveiro, Portugal. Professor há 27 anos, atualmente é docente titular do Instituto Federal de Educação, Ciência e Tecnologia de Mato Grosso do Sul (IFMS), Brasil. É secretário regional adjunto da Sociedade Brasileira de Computação (SBC) e membro da APM. |
CD 09 - E, ... entre pregos, martelos e microcomputadores, ... há 40 anos nasceu o PROFMATJosé Manuel Matos, Universidade Nova de Lisboa Terça-feira, 15 de julho, 15h00m - 16h00m Sala 295 Moderadora: Alexandra Sofia Rodrigues Público: Geral Resumo Em 1985 aconteceu o PROFMAT/85, primeiro congresso de professores de matemática em Portugal que constitui uma etapa na consolidação de uma identidade profissional dos professores que ensinam matemática e que lhes permitiu assumir uma maior autonomia, quer em relação aos poderes públicos, quer em relações a outras tutelas, nomeadamente as da comunidade académica. A conferência insere-se nas iniciativas do Grupo de Trabalho da APM sobre História e Memória do Ensino da Matemática para celebrar os 40 anos do PROFMAT e percorrerá cronologicamente os acontecimentos antecedentes, terminando com uma súmula do próprio encontro. Nota biográfica
José Manuel Matos – Iniciou a sua carreira na Escola do Magistério de Beja e foi professor de matemática do ensino secundário. Concluiu o mestrado na Universidade de Boston e o doutoramento na Universidade da Geórgia e durante vinte anos lecionou na Faculdade de Ciências e Tecnologia da Universidade Nova de Lisboa e mais tarde na Universidade Federal de Juiz de Fora, Brasil. Interessa-se atualmente por temas relacionados com as dimensões sociais, culturais e históricas no ensino e na aprendizagem da matemática. |
CD 10 - Capacidades matemáticas transversais: as novas brochuras para o Ensino BásicoAna Paula Canavarro, Universidade de Évora Segunda-feira, 14 de julho, 14h30m - 15h30m Anfiteatro 131 Público: Ensino Básico Resumo Recentemente, o Grupo de Trabalho do Desenvolvimento Curricular e Profissional em Matemática (GTDCPM) lançou cinco brochuras sobre as capacidades matemáticas no ensino básico, com o objetivo de facilitar a sua apropriação pelos professores dos diferentes níveis de ensino. Quatro brochuras são direcionadas para quatro níveis de ensino: 1.º e 2.º anos do 1.º ciclo; 3.º e 4.º anos do 1.º ciclo; 2.º ciclo e 3.º ciclo. A quinta brochura é especificamente direcionada ao Pensamento Computacional, por constituir maior novidade. Em cada brochura é clarificado o referencial que permite identificar as seis capacidades matemáticas como elementos relevantes na formação matemática dos alunos, incluindo exemplos de integração nas atividades a propor aos alunos. Nas diferentes brochuras são também analisadas tarefas propostas aos alunos das turmas da operacionalização antecipada das Aprendizagens Essenciais de Matemática para o Ensino Básico. Esta análise inclui, para cada tarefa, o enunciado, aspetos relacionados com a planificação da aula, relatos da sua concretização na prática e uma síntese dos conteúdos matemáticos e das capacidades matemáticas transversais promovidas. Nesta conferência apresentaremos as brochuras, explicando a estrutura dos documentos, a pertinência deste foco nas capacidades matemáticas que ilustraremos, ainda, com exemplos de tarefas e episódios presentes nas brochuras. Notas biográficas
Ana Paula Canavarro – Licenciada em Matemática pela Universidade de Lisboa (1986), com mestrado em Didática da Matemática pela Universidade de Lisboa (1993) e doutoramento em Educação Matemática pela Universidade de Lisboa (2004), Ana Paula Canavarro é Professora Associada no Departamento de Pedagogia e Educação da Universidade de Évora e membro integrado do Centro de Investigação em Psicologia e Educação (CIEP) da UÉ. Foi presidente da Sociedade Portuguesa de Investigação em Educação Matemática. Coautora do relatório Recomendações para a melhoria das aprendizagens dos alunos em Matemática (2018), coordenadora da equipa que redigiu as Aprendizagens Essenciais de Matemática para o Ensino Básico e integrou do grupo de trabalho que acompanhou as turmas que anteciparam a operacionalização do programa e conceberam o programa de formação contínua. Atualmente é Vice-Reitora para a Educação e Inovação Pedagógica da Universidade Évora.
Célia Mestre – Licenciada em Ensino da Matemática e Ciências da Natureza pela Escola Superior de Educação de Beja e Licenciada em Ciências da Educação com Mestrado na mesma área pela Faculdade de Psicologia e Ciências de Educação da Universidade de Lisboa, Doutorada em Educação na especialidade Didática da Matemática, pelo Instituto de Educação da Universidade de Lisboa e Pós-Graduação em Tecnologias e Metodologias da Programação no Ensino Básico, pela mesma instituição. Tem experiência na formação contínua e inicial de professores no âmbito da Didática da Matemática. Coautora do relatório Recomendações para a melhoria das aprendizagens dos alunos em Matemática (2018), coautora das Aprendizagens Essenciais de Matemática para o Ensino Básico e integrou o grupo de trabalho que acompanhou as turmas que anteciparam a operacionalização do programa e conceberam o programa de formação contínua. Com vasta experiência enquanto professora de 1.º Ciclo, atualmente é professora adjunta da Escola Superior de Educação de Setúbal.
Lina Brunheira – Licenciada em Ensino da Matemática e Mestre em Didática da Matemática pela Faculdade de Ciências da Universidade de Lisboa, Doutorada em Educação-Didática da Matemática pelo Instituto de Educação da Universidade de Lisboa. É coautora das Aprendizagens Essenciais de Matemática para o Ensino Básico e integrou o grupo de trabalho que acompanhou as turmas que anteciparam a operacionalização do programa e conceberam o programa de formação contínua. Atualmente é professora adjunta na Escola Superior de Educação de Lisboa onde se dedica à formação inicial de educadores e professores de 1.º e 2.º CEB.
Paulo Correia – Licenciado em Ensino de Matemática na Universidade de Évora, onde também concluiu o Curso de Especialização em Educação Matemática. É professor de Matemática do Ensino Básico e Secundário na Escola de Alcácer do Sal e desenvolve atividade como formador. Coautor do relatório Recomendações para a melhoria das aprendizagens dos alunos em Matemática (2018), das Aprendizagens Essenciais de Matemática para o Ensino Básico e do Ensino Secundário e integrou o grupo de trabalho que acompanhou as turmas que anteciparam a operacionalização do programa e conceberam o programa de formação contínua Mantém a página https://mat.absolutamente.net.
|
ProfMat 2025 - Sessões Práticas (2h)
As sessões práticas são propostas e dinamizadas por participantes no encontro, sobre temas, abordagens e materiais didáticos, em que é prevista a realização de trabalho prático e discussão, com um momento final para debate coletivo. Para além dos Grupos de trabalho e dos Parceiros da APM, qualquer participante pode submeter uma proposta de Sessão Prática (no separador "Profmat 2025").
|
SP 01 |
Avaliar para Pensar: Como Medir a Complexidade do Raciocínio Matemático? (Resumo) Cristina Caridade, Instituto Superior de Engenharia do Instituto Politécnico de Coimbra Público: 3º ciclo, Secundário e Superior |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 110 |
|
SP 02 |
Assobios e funções sinusoidais: actividades de modelação computacional (Resumo) Vitor Duarte Teodoro, Universidade Lusófona Público: Secundário |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 115 |
|
SP 03 |
Perspetivas de utilização do TI-Rover dos LEDs em situações de aprendizagem (Resumo) Eduardo Cunha, T3 Portugal Público: Básico e Secundário |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 106 |
|
SP 04 |
Práticas de utilização da tecnologia TI-Nspire CX nas Aprendizagens Essenciais de Matemática do Ensino Secundário (Resumo) Eduardo Cunha, T3 Portugal Público: Secundário |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 121 |
|
SP 05 |
A Matemática tem História (Resumo) Marisabel Antunes, Esc. Sec. D. Dinis, Coimbra Público: 3.º ciclo e Secundário |
Segunda-feira, 14 julho 14h30 - 16h30 |
Sala 119 |
|
SP 06 |
Azulejos e Matemática (Resumo) Helena Castro, Agrupamento Escolas Fernando Namora Público: 1.º, 2.º e 3.º ciclos |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 106 |
|
SP 07 |
Matemática fora da sala de aula: criar trilhos com o Math City Map (Resumo) Dora Vaz Pinto, Agrupamento de Escolas D. Luís de Ataíde (Peniche) Público: Todos os níveis de ensino Nota: Para esta sessão prática, é necessário trazer um portátil. |
Segunda-feira, 14 julho 14h30 - 16h30 |
Sala 122 |
|
SP 08 |
Matemática com Python no 10.º ano (Resumo) António Barral Cardoso, Agrupamento de Escolas de Reguengos de Monsaraz Público: Secundário |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 103 |
|
SP 09 |
Modelos Matemáticos para a Cidadania (Resumo) Dolcínia de Fátima Matos Almeida, Agrupamento de Escolas de Águeda Sul Público: Secundário |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 110 |
|
SP 10 |
O Python na Resolução de Problemas (em ambiente TI-Nspire) (Resumo) Jacinto Salgueiro, Agrupamento de escolas de Montemor-o-Novo Público: Secundário |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 103 |
|
SP 11 |
A calculadora gráfica NumWorks no ensino secundário (Resumo) Serenela Moreira, NumWorks Público: Secundário |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 119 |
|
SP 12 |
História das aproximações numéricas de π (Resumo) Sara Vaz Domingos, Universidade do Algarve Público: 3.º ciclo e Secundário |
Segunda-feira, 14 julho 14h30 - 16h30 |
Sala 103 |
|
SP 13 |
Geometria Sintética com o GeoGebra – Ir Mais Além (Resumo) José Carlos Pereira Público: Secundário |
Segunda-feira, 14 julho 14h30 - 16h30 |
Sala 106 |
|
SP 14 |
Conexões entre matemática e educação visual/expressão plástica (Resumo) Anabela Gaio, Agrupamento de Escolas de Camarate D' Nuno Alvares Pereira Público: 1.º e 2.º ciclos |
Segunda-feira, 14 julho 14h30 - 16h30 |
Sala 120 |
|
SP 15 |
Dobragens em Papel (Resumo) Ilda Rafael, Escola Secundária José Gomes Ferreira Público: Geral |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 115 |
|
SP 16 |
Corrida de Carros – usando Python e funções polinomiais e trigonométricas (Resumo) Sandra Gaspar Couto, Instituto Superior de Engenharia de Lisboa Público: Secundário |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 122 |
|
SP 17 |
Ó Zé como resolverias este problema... (Resumo) Mária Cristina Almeida, CICS.NOVA (Centro Interdisciplinar de Ciências Sociais) Público: 3.º ciclo e Secundário |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 119 |
|
SP 18 |
Álgebra de Boole: Play & Win (Resumo) Cristina Maria Bata Fernandes, Agrupamento de Escolas de Sampaio Público: Cursos Profissionais |
Segunda-feira, 14 julho 14h30 - 16h30 |
Sala 121 |
|
SP 19 |
As tarefas de modelação nas Aprendizagens Essenciais do Ensino Secundário (Resumo) António Júlio Aroeira, Escola Básica e Secundária da Madalena, Açores Público: Secundário |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 120 |
|
SP 20 |
4 M’S Mente, Música, Matemática e Movimento (Resumo) Ana Mafalda Sousa, Agrupamento de Escolas de Ovar Público: 1.º ciclo |
Segunda-feira, 14 julho 14h30 - 16h30 |
Sala 110 |
|
SP 21 |
Apps for Good - Giving young people the skills to shape their future (Resumo) Matilde Buisel, CDI Portugal Público: 2.º e 3.º ciclos e Secundário |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 120 |
|
SP 22 |
A experimentação da Plataforma Mathigon no ensino de Geometria (Resumo) Lialda Bezerra Cavalcanti, Instituto Federal de Educação, Ciência e Tecnologia de Pernambuco / Unidade de Investigação e Desenvolvimento em Educação e Formação (UIDEF) Público: 3.º ciclo e Secundário |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 296 |
|
SP 23 |
Resolução de problemas de Geometria e Funções com o GeoGebra: Representações múltiplas (Resumo) Cristina Negra, Escola Básica e Secundária de Gama Barros Público: Secundário |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 121 |
|
SP 24 |
Pavimentações com ferramentas GeoGebra (Resumo) Carla Faneco, Agrupamento de Escolas de Sampaio Público: 2.º e 3.ºciclos |
Segunda-feira, 14 julho 14h30 - 16h30 |
Sala 296 |
|
SP 25 |
MILAGE Aprender+ versão 2.0: Personalização, Autonomia e Inovação no Ensino da Matemática (Resumo) Mauro Figueiredo, Universidade do Algarve Público: Básico e Secundário |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 122 |
|
SP 26 |
Recursos digitais e interativos para a Matemática no 3º Ciclo e Ensino Secundário (Resumo) Associação Atractor – Matemática Interactiva Público: 3.º ciclo e Secundário |
Segunda-feira, 14 julho 14h30 - 16h30 |
Sala 297 |
|
SP 27 |
Ensinar a Programar através da Matemática (Resumo) Andreia Mordido, Faculdade de Ciências, Universidade de Lisboa Público: 3.º ciclo e Secundário |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 296 |
|
SP 28 |
Matemática: caminhos traçados pela curiosidade (Resumo) Beatriz Barradas David, Universidade de Évora Público: 1.º ciclo |
Terça-feira, 15 julho 10h30 - 12h30 |
Sala 297 |
|
SP 29 |
O processo de ensino e aprendizagem da Combinatória: uma experiência de ensino (Resumo) Mónica Valadão, Escola Básica e Secundária Tomás de Borba, Terceira, Açores; Público: Secundário |
Terça-feira, 15 julho 14h00 - 16h00 |
Sala 297 |
RESUMOS
SP 01 - Avaliar para Pensar: Como Medir a Complexidade do Raciocínio Matemático?Cristina Caridade, Instituto Superior de Engenharia do Instituto Politécnico de Coimbra Terça-feira, 15 de julho, 14h00m - 16h00m Resumo Será que as nossas questões de avaliação exploram verdadeiramente os diferentes níveis de pensamento dos alunos? Avaliamos só o que sabem ou também como pensam? Notas biográficas Cristina Caridade - Professora Coordenadora no Departamento de Física e Matemática do Instituto Superior de Engenharia de Coimbra – IPC, doutorada em Matemática Aplicada. Desenvolve investigação nas áreas de processamento digital de imagem e de ensino da matemática, com enfoque em gamificação, jogos educativos, PBL e atividades STEM. Participa em projetos Erasmus+ sobre avaliação de competências matemáticas, aprendizagem em serviço e escape rooms digitais no ensino superior. Verónica Pereira - Doutorada em Didática da Matemática. Com uma carreira sólida no ensino da matemática. Tem experiência no Ensino Superior, Ensino Secundário e Ensino Básico. Demonstra um foco claro na avaliação educacional em matemática e na melhoria das práticas de ensino. A sua atuação abrange diferentes níveis de ensino e instituições (IPC, IPV, IPG, Universidade Católica), refletindo um compromisso com a qualidade e inovação na educação matemática. José Alexandre Martins - Professor Adjunto no Departamento de Ciências Exatas e Experimentais do Instituto Politécnico da Guarda – IPG, doutorado em Didática de Ciências e Tecnologias - Especialização em Didática de Ciências Matemáticas pela UTAD. Desenvolve investigação, entre outras, na área do ensino da estatística, com foco na utilização da tecnologia e em particular com a geometria dinâmica |
SP 02 - Assobios e funções sinusoidais: actividades de modelação computacionalVitor Duarte Teodoro, Universidade Lusófona Terça-feira, 15 de julho, 10h30m - 12h30m Resumo Este workshop de 2 horas visa explorar a modelação computacional de fenómenos ondulatórios, com foco na análise de assobios através de funções sinusoidais. Aborda conceitos fundamentais como radianos, frequência angular, funções trigonométricas e as suas aplicações práticas. Nota biográfica Vítor Duarte Teodoro - Especialista em educação em ciências, com mais de 40 anos de experiência no ensino da Física, Matemática e Ciências da Computação, bem como na formação de professores a nível nacional e internacional. Doutorado em Educação (Teoria Curricular e Educação em Ciências) pela Universidade Nova de Lisboa, coordenou programas de formação de professores e desenvolveu investigação em modelação matemática e tecnologia educativa. Autor de software educacional, publicado em Portugal, nos EUA e em diversos outros países, publicou numerosos manuais escolares e artigos científicos. Foi consultor para reformas educacionais, desenho de laboratórios escolares e recursos digitais, colaborando com instituições governamentais e internacionais. Além da sua experiência no ensino superior e secundário, teve um papel ativo em redes profissionais e projetos interdisciplinares na Europa e América Latina. |
SP 03 - Perspetivas de utilização do TI-Rover dos LEDs em situações de aprendizagemEduardo Cunha, T3 Portugal Terça-feira, 15 de julho, 14h00m - 16h00m Resumo Todas as Escolas do país, sem exceção, têm agora a oportunidade de promover a aprendizagem dos seus alunos com recurso a dispositivos tecnológicos disponibilizados no âmbito dos LED (Laboratórios de Educação Digital da DGE). Em particular, os professores de matemática podem tirar partido de ambientes de aprendizagem, ativos e motivadores, proporcionados pela utilização pedagógica dos LEDs, nomeadamente com tarefas de aprendizagem com recurso ao dispositivo robótico TI-Rover e à interface TI-HUB. Nesta sessão procurar-se-á, com experiências práticas, dar resposta à questão “Como podem desenvolver-se aprendizagens matemáticas, sejam elas mais focadas no conhecimento, nos procedimentos ou nas competências/ideias chave das AEs de Matemática?”. Nota: Serão fornecidas calculadoras gráficas TI-Nspire CX II-T e dispositivos TI-Rover, mas os participantes poderão trazer a sua calculadora gráfica e/ou software atualizado e o TI-Rover e Hub que fazem parte do LED da sua escola. Notas biográficas Eduardo Cunha - Membro do grupo de trabalho T3 da APM, Mestre em Tecnologia Educativa, Formador das AEs de Matemática do 3.ºCiclo do Ensino Básico e do Ensino Secundário, Professor do Agrupamento de Escolas de Barcelos. Raul Aparício Gonçalves - Membro do grupo de trabalho T3 da APM, do grupo de trabalho de Desenvolvimento Curricular e Profissional em Matemática para o Ensino Secundário e professor de uma turma experimental de matemática A das novas AEs de matemática A no AE de Ermesinde. |
SP 04 - Práticas de utilização da tecnologia TI-Nspire CX nas Aprendizagens Essenciais de Matemática do Ensino SecundárioEduardo Cunha, T3 Portugal Terça-feira, 15 de julho, 10h30m - 12h30m Resumo A tecnologia TI-Nspire CX tem características únicas que a tornam um instrumento tecnológico de aprendizagem versátil e eficiente. Nesta sessão serão trabalhadas tarefas de aprendizagem baseadas nas desenvolvidas pelos professores das turmas piloto de matemática A, com as quais se irá propor que os participantes experienciem o trabalho com este tipo de tecnologia e percecionem as vantagens e a mais-valia nas aprendizagens matemáticas. Nota: Serão fornecidas calculadoras gráficas TI-Nspire CX II-T, mas deverá ser utilizado, com vantagem, os portáteis dos participantes com o respetivo software instalado e atualizado. Os participantes que tiverem algum conhecimento desta tecnologia, mesmo que a nível bastante básico, beneficiarão no acompanhamento dos trabalhos. Notas biográficas Eduardo Cunha - Membro do grupo de trabalho T3 da APM, Mestre em Tecnologia Educativa, Formador das AEs de Matemática do 3.ºCiclo do Ensino Básico e do Ensino Secundário, Professor do Agrupamento de Escolas de Barcelos. Raul Aparício Gonçalves - Membro do grupo de trabalho T3 da APM, do grupo de trabalho de Desenvolvimento Curricular e Profissional em Matemática para o Ensino Secundário e professor de uma turma experimental de matemática A das novas AEs de matemática A no AE de Ermesinde. |
SP 05 - A Matemática tem HistóriaMarisabel Antunes, Esc. Sec. D. Dinis, Coimbra Segunda-feira, 14 de julho, 14h30m - 16h30m Resumo A História da Matemática é uma das nove ideias-chave das Novas Aprendizagens Essenciais. Nota biográfica Marisabel Antunes - Licenciada em Matemática – Ramo de Formação Educacional pela Faculdade de Ciências e Tecnologia da Universidade de Coimbra (1994); Mestre em Ensino de Matemática no 3.º ciclo do Ensino Básico e no Secundário pela Faculdade de Ciências e Tecnologia da Universidade de Coimbra – Principal área: Formação de Professores (2012); e Doutoranda do Programa Doutoral em Didática de Ciências e Tecnologia na Especialidade de Didática de Ciências Matemáticas, na Universidade de Trás os Montes e Alto Douro. Professora de duas turmas piloto do 11.º Ano de Matemática A, na Escola Secundária D. Dinis em Coimbra. Jaime Carvalho e Silva - Professor Associado do Departamento de Matemática da FCT da Universidade de Coimbra. Membro do Centro de Investigação Matemática CMUC (UC). Responsável por disciplinas do 1º ano de cursos de Engenharia/Ciências/Gestão e do Mestrado em Ensino de Matemática da FCTUC. Docente do Programa de Doutoramento em História das Ciências e Educação Científica. Coordenador do Mestrado em Ensino de Matemática para o 3º Ciclo do Ensino Básico e Ensino Secundário da FCTUC. Autor de textos para o Ensino Básico, Secundário e Superior. Premiado duas vezes com o prémio Sebastião e Silva da SPM para manuais escolares. Co-autor dos programas de Matemática para o Ensino Secundário de 1997, 2001 e 2023, incluindo Matemática A e B, MACS e Matemática dos Cursos Profissionais e Artísticos. Coordenador do Grupo de Trabalho de Matemática nomeado pelo ME (2018-2020) e que publicou um documento com “Recomendações". Membro da Comissão Executiva e Secretário-Geral do ICMI-Comissão Internacional para a Instrução Matemática (2008-2010 e 2010-2012 respetivamente). Participou na elaboração de vários estudos do ICMI, nomeadamente os relativos ao uso da História da Matemática no Ensino, ao Ensino Superior de Matemática, às Inovações Curriculares e ao Ensino da Geometria. |
SP 06 - Azulejos e MatemáticaHelena Castro, Agrupamento Escolas Fernando Namora Terça-feira, 15 de julho, 10h30m - 12h30m Resumo Nesta sessão vamos trabalhar e explorar de forma diferenciada as isometrias com atividades adequadas a cada um dos três níveis de ensino. Pretende-se dinamizar, em conexão com a área de Artes Visuais, a construção de um painel em papel e/ou GeoGebra, azulejos, recorrendo a um motivo que se possa reproduzir em diversas posições relacionadas umas com as outras e gerando distintos efeitos, como é o caso do azulejo de Eduardo Nery. Pretende-se proporcionar o uso de um ambiente de geometria dinâmica (AGD) para explorar, a pares, a reflexão e rotação de figuras planas e discutir os resultados obtidos. Pretende-se estabelecer conexões que envolvam frisos ou padrões, evidenciando a relevância da Matemática na criação e construção do mundo que nos rodeia. Notas biográficas Helena Castro - Licenciada em Ensino da Matemática, pela Faculdade de Ciências de Lisboa (1997), Pós-Graduação em Novas Tecnologias Aplicadas à Educação e Formação, pelo Instituto Superior de Educação e Ciências, (2008) e doutoranda em Educação – Didática da Matemática, pelo Instituto de Educação, é professora do grupo 500 desde 1988. Em 1997, tornou-se professora no Agrupamento de Escolas Fernando Namora, Amadora, onde tem desempenhado diversos cargos nomeadamente membro das equipas STEAM e PADDE e Coordenadora de Projetos, dinamizadora do projeto Arte e Ciência, entre outros. Colaboradora do GI2 da FCUL. Susana Teixeira - Licenciada em Arquitectura, pela Faculdade Lusíada de Lisboa (1998), profissional liberal em Arquitectura com inscrição na Ordem dos Arquitectos de Lisboa, é professora do grupo 600 (Artes Visuais), desde 1998. Em 2019, tornou-se professora no Agrupamento de Escolas Fernando Namora, Amadora, onde tem desempenhado funções de docente nas disciplinas de Educação Visual, Desenho A e Geometria Descritiva A. Para além das funções docentes, tem desempenhado cargos, tais como dinamizadora do projeto Arte e Ciência, membro da equipa de projetos, equipa STEAM e coordenadora do Plano Nacional das Artes. Marisabel Antunes - Licenciada em Matemática – Ramo de Formação Educacional pela Faculdade de Ciências e Tecnologia da Universidade de Coimbra (1994); Mestre em Ensino de Matemática no 3.º ciclo do Ensino Básico e no Secundário pela Faculdade de Ciências e Tecnologia da Universidade de Coimbra – Principal área: Formação de Professores (2012); e Doutoranda do Programa Doutoral em Didática de Ciências e Tecnologia na Especialidade de Didática de Ciências Matemáticas, na Universidade de Trás os Montes e Alto Douro. Professora de duas turmas piloto do 11.º Ano de Matemática A, na Escola Secundária D. Dinis em Coimbra. |
SP 07 - Matemática fora da sala de aula: criar trilhos com o Math City MapDora Vaz Pinto, Agrupamento de Escolas D. Luís de Ataíde (Peniche) Segunda-feira, 14 de julho, 14h30m - 16h30m Resumo Será que a Matemática está em todo o lado? Para os alunos conseguirem ver a matemática que os rodeia, é necessário que o professor os ensine a ver. A criação de tarefas em contexto real, fora da sala de aula, promove a formulação e resolução de problemas, o estabelecimento de conexões matemáticas, o pensamento crítico, mas também o trabalho colaborativo e a criatividade, indo assim ao encontro das orientações das Aprendizagens Essenciais para o Ensino Básico e o Ensino Secundário. O recurso à tecnologia, e em particular à aplicação Math City Map (disponível gratuitamente em qualquer smartphone) torna a criação de tarefas e, posteriormente, a exploração de trilhos, muito mais dinâmicos e motivadores para os alunos. Nesta sessão prática, iremos explicar como criar tarefas matemáticas no computador, no portal Math City Map (https://mathcitymap.eu/pt/). Veremos ainda como criar trilhos matemáticos e como explorar estes percursos na aplicação Math City Map, no telemóvel. Nota: Para esta sessão prática, é necessário trazer um portátil. Notas biográficas Dora Vaz Pinto - Licenciada em Matemática (Ramo de Formação Educacional), pela Universidade do Algarve e Pós-Graduada em Matemática Aplicada, pela Universidade Lusíada. Docente de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário, desde 2004, atualmente no Agrupamento de Escolas D. Luís de Ataíde (Peniche). Manuel João Marques - Licenciado em Matemática Ramo Educacional, pela Faculdade de Ciências da Universidade de Coimbra. Docente de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário, desde 2001, atualmente na Escola Secundária Domingos Sequeira (Leiria). Coautor de manuais escolares do 3.º Ciclo, entre 2001 e 2012. Formador acreditado pelo Conselho Científico-Pedagógico da Formação Contínua, desde 2013. Atualmente, é Vice-presidente da Associação de Professores de Matemática (APM) e coordenador do Grupo de Trabalho CASIO+ da APM. |
SP 08 - Matemática com Python no 10.º anoAntónio Barral Cardoso, Agrupamento de Escolas de Reguengos de Monsaraz Terça-feira, 15 de julho, 14h00m - 16h00m Resumo O pensamento computacional permite desenvolver competências que serão essenciais no futuro. Segundo as Aprendizagens Essenciais de Matemática – 10.º ano, “Os aspetos comuns entre o Pensamento Matemático e o Pensamento Computacional, bem como a relevância atual do Pensamento Computacional na ciência e na sociedade, justificam que o currículo de Matemática valorize esta abordagem conceptual na resolução de problemas”. A linguagem de programação Python é uma das mais populares e das mais usadas em todo o mundo, por estudantes e programadores profissionais. Esta Sessão Prática é uma iniciação a esta linguagem, com recurso à calculadora gráfica CASIO fx-CG50. Nota: os participantes devem ser portadores de computores portáteis. Notas biográficas António Barral Cardoso - Licenciado em Ensino de Matemática e possui o curso de especialização do Mestrado em Educação Matemática, pela Universidade de Évora. É professor do ensino básico (3.º ciclo) e secundário. Foi professor de uma turma de antecipação da generalização das novas Aprendizagens Essenciais (3.º ciclo). Desenvolve também atividade ao nível da formação de professores e é membro do Grupo de Trabalho CASIO+ da APM. Manuel João Marques - Licenciado em Matemática Ramo Educacional, pela Faculdade de Ciências da Universidade de Coimbra. Docente de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário, desde 2001, atualmente na Escola Secundária Domingos Sequeira (Leiria). Coautor de manuais escolares do 3.º Ciclo, entre 2001 e 2012. Formador acreditado pelo Conselho Científico-Pedagógico da Formação Contínua, desde 2013. Atualmente, é Vice-presidente da Associação de Professores de Matemática (APM) e coordenador do Grupo de Trabalho CASIO+ da APM. |
SP 09 - Modelos Matemáticos para a CidadaniaDolcínia de Fátima Matos Almeida, Agrupamento de Escolas de Águeda Sul - Escola Secundária Marques de Castilho Terça-feira, 15 de julho, 10h30m - 12h30m Resumo No currículo das Novas Aprendizagens Essenciais de Matemática para o Ensino Secundário surge como ideia inovadora a “Matemática para a cidadania” a qual se pretende que faça parte integrante da formação geral dos jovens. Assim sendo, nesta sessão prática pretende-se explorar alguns modelos matemáticos de processos eleitorais e de modelos financeiros usando as potencialidades da tecnologia, em particular, da calculadora gráfica, na resolução de problemas. No que se refere a ideias chave das aprendizagens essenciais destaca-se o “Recurso sistemático à tecnologia” uma vez que as tarefas previstas promovem a exploração de ideias e conceitos, integrando a tecnologia como alavanca para a compreensão e resolução de problemas. Nesta sessão será ainda abordada uma iniciação à programação em Python, aplicada em tarefas que promovem o desenvolvimento de processos algorítmicos, o pensamento estruturado e o raciocínio lógico, para a resolução de problemas, para além do desenvolvimento do pensamento computacional. Notas biográficas Dolcínia de Fátima Matos Almeida - Licenciada e Mestre em Ensino da Matemática. Certificada como formadora na área e domínio das Didáticas Específicas da Matemática desde 2000. Professora Acompanhante Local do Programa Ajustado de Matemática no ensino secundário em 1999; Professora Acompanhante do Plano de Ação para a Matemática no ensino Básico. Desde 2012 integra o grupo de Trabalho Casio +. Paula Cristina Antunes Teixeira - Licenciada em Ensino da Matemática, Mestre e Doutorada em Ciências da Educação. Certificada como formadora na área e domínio das Didáticas Específicas da Matemática desde 2000. Professora Acompanhante Local do Programa Ajustado de Matemática no ensino secundário em 1999; Professora Acompanhante do Plano de Ação para a Matemática no ensino Básico. Leciona desde o ano letivo transato uma turma-piloto de Matemática A, das Novas Aprendizagens Essenciais de Matemática para o Ensino Secundário. Desde 2022 integra o grupo de Trabalho Casio +. |
SP 10 - O Python na Resolução de Problemas (em ambiente TI-Nspire)Jacinto Salgueiro, Agrupamento de escolas de Montemor-o-Novo Terça-feira, 15 de julho, 10h30m - 12h30m Resumo Esta sessão prática destina-se a professores de Matemática e tem como principal objetivo promover a integração da linguagem Python na resolução de problemas matemáticos, tirando partido das potencialidades da calculadora TI-Nspire CXII. Uma vez que esta tecnologia permite interligar os vários ambientes de trabalho (Python, Listas e Folha de Cálculo, Dados e Estatística, Gráficos e Calculadora) será proposta a resolução de problemas onde se pode tirar partido desta potencialidade. Nota: os participantes devem ser portadores de computores portáteis. Notas biográficas Jacinto Salgueiro - Licenciatura em Ensino de Matemática – Faculdade de Ciências de Lisboa. Formador do Grupo de Trabalho T3 da APM. Simone Azevedo - Licenciatura em Matemática (ensino de) – Universidade de Trás-os-Montes e Alto Douro. Mestre em Matemática para o Ensino – Universidade do Algarve. Formadora do Grupo de Trabalho T3 da APM. |
SP 11 - A calculadora gráfica NumWorks no ensino secundárioSerenela Moreira, NumWorks Terça-feira, 15 de julho, 10h30m - 12h30m Resumo Nesta sessão prática, iremos explorar a tecnologia da calculadora gráfica NumWorks e a sua utilidade no ensino das disciplinas de matemática do Ensino Secundário. Os participantes poderão descobrir como pode a NumWorks facilitar a dinâmica de sala de aula, graças ao seu design intuitivo e facilidade de utilização, que dispensa manual de instruções. Notas biográficas Serenela Moreira - Responsável pela relação com os professores na NumWorks há mais de 5 anos. É apaixonada por matemática e lida diariamente com dezenas de docentes, aos quais dá formação e apoio na utilização da calculadora. Graças ao seu contacto com docentes, trabalha também diretamente com a equipa de engenheiros da NumWorks para desenvolver novas aplicações e garantir que a calculadora se encontra perfeitamente adaptada ao currículo em Portugal. |
SP 12 - História das aproximações numéricas de πSara Vaz Domingos, Universidade do Algarve Segunda-feira, 14 de julho, 14h30m - 16h30m Resumo O fascínio pelo conhecimento do valor numérico da constante real que hoje denotamos por π é transversal à história do Homem. Desde as primeiras aproximações, atribuídas aos babilónios, que inúmeros cientistas dedicaram uma parte significativa da sua vida a tentar obter novos métodos que permitissem conhecer o valor numérico deste número irracional. Alguns desses trabalhos são tão importantes que se tornaram marcos proeminentes na história da Matemática, como são exemplo, o método da exaustão, apresentado por Arquimedes, a primeira fórmula direta, atribuída a François Viète, a revolucionária contribuição de Isaac Newton, entre tantas outras que são impossíveis de mencionar no espaço limitado para este resumo. Nota: os participantes devem ser portadores de computores portáteis. Notas biográficas Sara Vaz Domingos - Aluna do Mestrado em Ensino de Matemática na NOVA-FCT. Licenciada em Matemática Aplicada à Economia e à Gestão pela Universidade do Algarve. Ana Rita Teixeira - Aluna da Pós-Graduação em Matemática para o Ensino. Celestino Coelho - Doutorado em Matemática. Docente no Departamento de Matemática da Faculdade de Ciência e Tecnologia na Universidade do Algarve. Maria da Graça Marques - Doutorada em Matemática. Docente no Departamento de Matemática da Faculdade de Ciência e Tecnologia na Universidade do Algarve. |
SP 13 - Geometria Sintética com o GeoGebra – Ir Mais AlémJosé Carlos Pereira Segunda-feira, 14 de julho, 14h30m - 16h30m Resumo A Geometria Sintética é um dos tópicos das Aprendizagens Essenciais de Matemática A do Ensino Secundário (AE). No âmbito do tema da Geometria Sintética, como Ação Estratégica do Professor, as AE sugerem a exibição relações métricas entre os pontos notáveis, por exemplo: a distância do ortocentro ao baricentro é o dobro da distância do baricentro ao circuncentro ou que o centro da circunferência de nove pontos é o ponto médio do segmento definido pelo circuncentro e pelo ortocentro. Nesta Sessão Prática iremos trabalhar tarefas sobre algumas destas propriedades. Usaremos o GeoGebra para as conjeturar e, em seguintes, tentaremos a sua prova. Todas as tarefas a realizar poderão ser utilizadas em contexto de sala de aula. Não é necessário ser um utilizador experiente do GeoGebra para poder frequentar esta sessão. Como pré-requisito é apenas necessário saber o processo de construção dos quatro pontos notáveis presentes no Programa, Incentro, Circuncentro, Baricentro e Ortocentro. Nota: os participantes devem ser portadores de computores portáteis. Nota biográfica José Carlos Pereira - Professor de Matemática, licenciado pela Faculdade de Ciências da Universidade de Lisboa com estágio profissional na Escola Secundária Seomara da Costa Primo. Dedica-se ao seu centro de explicações de Matemática desde então. É administrador do grupo de Facebook Recursos para Matemática, onde gere e fomenta a partilha e discussão de temas relacionados com a Matemática e a sua docência entre mais de 9000 membros. Coautor do livro de apoio escolar Preparar o Exame Matemática A, da Raiz Editora e do manual Matemática 360 da mesma editora. Colaborador do Clube de Matemática da Sociedade Portuguesa de Matemática, com a coluna «Se e só se». |
SP 14 - Conexões entre matemática e educação visual/expressão plásticaAnabela Gaio, Agrupamento de Escolas de Camarate D' Nuno Alvares Pereira Segunda-feira, 14 de julho, 14h30m - 16h30m Resumo As aprendizagens essenciais indicam que aprender matemática tem como objetivo entre outros, desenvolver a capacidade de estabelecer conexões matemáticas. As conexões externas da Matemática com várias áreas do conhecimento, possibilitam que os conhecimentos matemáticos sejam usados para compreender, modelar e atuar em várias áreas. Nos Princípios e Normas para a Matemática Escolar (NCTM com tradução APM 2008), afirma-se que ao estabelecerem conexões os alunos desenvolvem uma compreensão mais profunda da matemática. Susana Carreira no editorial da revista Educação e Matemática (2010), afirma que não basta ver as conexões matemáticas, mas que “é necessário fazê-las”, permitindo que os alunos estabeleçam relações entre temas, conceitos, representações e processos internos à própria matemática, mas também entre a matemática e a realidade ou com outras áreas de conhecimento. Seguindo a lógica da integração de saberes vão trabalhar-se alguns dos dominios das AE em simultâneo, sendo ainda solicitado aos participantes que reflitam noutras possibilidades. Iremos apresentar tarefas que tem inerente uma metodologia de aprendizagem ativa. Notas biográficas Anabela Moreira Gaio - Licenciatura em Ensino Básico variante Matemática e Ciências - Escola Superior de Educação de Lisboa. Formadora acreditada pelo CCPFC nas áreas de didáticas especificas - matemática e métodos quantitativos. Formadora do Programa de Formação Continua em Matemática – equipa da Escola Superior de Educação de Lisboa e de Ações de Formação no âmbito do “Novo Programa de Matemática (programa de 2007)” - DGIDC. Susana Cristina Cordeiro Serra - Licenciatura em Ensino Básico variante Matemática e Ciências - Escola Superior de Educação Jean Piaget de Almada. Mestrado em Educação Matemática - Escola Superior de Educação de Lisboa. Formadora nas áreas de: didática geral e didáticas especificas (matemática e ciências da natureza) tendo dinamizado ações de Formação no âmbito das AE de matemática em vigor – DGE. |
SP 15 - Dobragens em PapelIlda Rafael, Escola Secundária José Gomes Ferreira Terça-feira, 15 de julho, 14h00m - 16h00m Resumo As dobragens em papel constituem uma ferramenta didática muito versátil para estudar conceitos matemáticos e também para promover atividades de cidadania, uma vez que estimula a reutilização do papel para fins lúdicos e didáticos. Notas biográficas Ilda Rafael - Professora de Matemática, licenciada pela Faculdade de Ciências da Universidade de Lisboa, leciona no Agrupamento de Escolas de Benfica, na Escola Secundária José Gomes Ferreira, no ensino secundário. Coordena o projeto Origami no Agrupamento, que envolve alunos de todos os ciclos. Colabora regularmente com a APM e com a Ludus, nomeadamente na Feira da Matemática e na Noite Europeia dos Investigadores, com diversas Escolas e Associações promovendo a pratica do Origami como recurso lúdico e didático para apender Matemática e com os Origamigos de Lisboa, coordenando a participação no Iberanime e nos encontros mensais. Anabela Moreira Gaio - Licenciatura em Ensino Básico variante Matemática e Ciências - Escola Superior de Educação de Lisboa. Formadora acreditada pelo CCPFC nas áreas de didáticas específicas - matemática e métodos quantitativos. |
SP 16 - Corrida de Carros – usando Python e funções polinomiais e trigonométricasSandra Gaspar Couto, Instituto Superior de Engenharia de Lisboa Terça-feira, 15 de julho, 10h30m - 12h30m Resumo Os meus alunos fazem este trabalho que é uma corrida de carros usando programação em Python. Também pode ser uma joaninha a percorrer um prado verdejante, etc. É muito atrativo para eles. Os alunos escolhem uma pista e um carro de que gostem. Eu forneço aos alunos o programa em que o meu carro percorre a minha pista, eles só alteram para ser o carro deles a percorrer a pista deles. A parte de Python é simples e já está feita, na prática só têm de manipular a matemática. Nota: os participantes devem ser portadores de computores portáteis. Nota biográfica Sandra Gaspar Couto - Docente de matemática do Instituto Superior de Engenharia de Lisboa desde 2000. Foi docente do ensino básico durante 3 anos. É doutorada em Ciências da Educação pela Universidade Nova de Lisboa. Um grande foco do seu trabalho é tirar partido da tecnologia para fomentar a aprendizagem significativa dos alunos. |
SP 17 - Ó Zé como resolverias este problema...Mária Cristina Almeida, CICS.NOVA (Centro Interdisciplinar de Ciências Sociais) Terça-feira, 15 de julho, 14h00m - 16h00m Resumo No princípio dos anos 80, existia entre os professores de Matemática um forte sentimento de crítica às condições de ensino nas escolas portuguesas. Uma das orientações curriculares propostas na altura dava grande relevo ao papel dos problemas no sentido de desenvolver o espírito de investigação e descoberta. 40 anos depois a resolução de problemas continua a ser fundamental na aprendizagem dos alunos, e um dos aspetos mais desafiadores em sala de aula. Nesta Sessão Prática pretendemos cativar-vos para a importância de desenvolver o conhecimento matemático articulando e interligando entre diversos saberes, numa perspetiva que tenha por base a participação ativa do estudante, em situações que desenvolvam o seu raciocínio. Os problemas que vos proporemos são intemporais, podem ser abordados em vários ciclos de ensino, em contexto de sala de aula e em atividades extracurriculares. Notas biográficas Mária Cristina Almeida - Licenciada em Matemática, Mestre e Doutora em Ciências da Educação. É professora de Matemática no ensino secundário e investigadora na UIED e no CICS.NOVA. O seu principal interesse de investigação é a História da Educação Matemática, particularmente formação de professores, desenvolvimento curricular e livros didáticos. É membro coordenador do Grupo de Trabalho sobre História e Memórias do Ensino da Matemática, da APM. Ana Lopes - Licenciada em Matemática, ramo de Investigação Operacional pela NOVA FCT, Mestre em Estatística e Gestão da Informação pela NOVA IMS e Mestre em Ensino da Matemática no 3.º Ciclo e Ensino Secundário pela NOVA FCT. Exerce funções docentes na Escola Básica e Secundária Francisco Simões. Os seus principais interesses de investigação prendem-se com questões ligadas à Educação. Membro do Grupo de Trabalho sobre História e Memórias do Ensino da Matemática, da APM. |
SP 18 - Álgebra de Boole: Play & WinCristina Maria Bata Fernandes, Agrupamento de Escolas de Sampaio Segunda-feira, 14 de julho, 14h30m - 16h30m Resumo O objetivo desta sessão prática é familiarizar os professores de Matemática com as aplicações Academo Logic Gate e Mathigon, explorando tarefas da Coletânea do módulo OP12 – Álgebra de Boole, já testadas em turmas piloto. Em formato hands-on e com uma abordagem gamificada, os participantes resolverão desafios interativos que evidenciam o potencial destas ferramentas para desenvolver o pensamento computacional. Pretende-se aumentar a motivação, promover a inclusão de diferentes recursos e estilos de aprendizagem e reforçar as competências definidas nas Aprendizagens Essenciais. Através de atividades dinâmicas, descobriremos formas criativas de integrar elementos lúdicos no ensino da Matemática, tornando-o mais envolvente e memorável para os alunos. Nota: os participantes devem ser portadores de computores portáteis. Notas biográficas Cristina Maria Bata Fernandes - Licenciada em Ensino da Matemática pela Faculdade de Ciências da Universidade de Lisboa e concluiu o primeiro ano do Mestrado em Educação, na área de especialização em Formação e Aprendizagem ao Longo da Vida, na FCUL. É docente do Agrupamento de Escolas de Sampaio e é professora de uma turma piloto das AE para os Cursos Profissionais e co-autora das Coletâneas de Tarefas aplicadas nas turmas piloto de Matemática B e Cursos Profissionais do ensino secundário, desde 2023. Elsa Maria Cardoso Gomes - Licenciada em Matemática, Ramo Educacional pela Faculdade de Ciências da Universidade do Porto (FCUP) e concluiu o primeiro ano do Mestrado em Deteção Remota, na FCUP. É docente da Escola Secundária de Paços de Ferreira. É professora de uma turma piloto das AE para os Cursos Profissionais e co-autora das Coletâneas de Tarefas aplicadas nas turmas piloto de Matemática B e Cursos Profissionais do ensino secundário, desde 2023. Marília André do Rosário - Licenciada em Matemática pela Faculdade de Ciências da Universidade do Porto e Mestre em Supervisão Pedagógica em Ensino da Matemática pela Universidade do Minho. É docente do Agrupamento de Escolas Tomaz Pelayo. Foi Professora Acompanhante do Plano de Ação para a Matemática, Supervisora no Processo de classificação de Provas do IAVE, orientadora de estágio da FCUP e UM, formadora acreditada pelo CCPFC e é professora de uma turma piloto das AE para os Cursos Profissionais e co-autora das Coletâneas de Tarefas aplicadas nas turmas piloto de Matemática B e Cursos Profissionais do ensino secundário, desde 2023. |
SP 19 - As tarefas de modelação nas Aprendizagens Essenciais do Ensino SecundárioAntónio Júlio Aroeira, Escola Básica e Secundária da Madalena, Açores Terça-feira, 15 de julho, 10h30m - 12h30m Resumo As Aprendizagens Essenciais de Matemática seguem a tendência internacional na relevância atribuída à modelação matemática no processo de ensino e aprendizagem dos alunos: Nota: os participantes devem ser portadores de uma calculadora gráfica. Nota biográfica António Júlio Aroeira - Professor de Matemática, Licenciado em Matemática pela Faculdade de Ciências da Universidade de Lisboa. Atualmente leciona na Escola Básica e Secundária da Madalena. Integrou as equipas de Acompanhamento Local do Programa de Matemática (1998-2022) e de Formação e Acompanhamento do Ensino Básico na R. A. dos Açores (2013-2021). Frequenta o Programa Doutoral em Didática da Matemática na Faculdade de Ciências da Universidade de Lisboa, desenvolvendo a sua tese no âmbito da Modelação Matemática. |
SP 20 - 4 M’S Mente, Música, Matemática e MovimentoAna Mafalda Sousa, Agrupamento de Escolas de Ovar Segunda-feira, 14 de julho, 14h30m - 16h30m Resumo O objetivo desta sessão é trabalhar áreas da matemática, tendo por princípio os objetivos das aprendizagens essências, como fomentar uma predisposição positiva para a aprendizagem, desenvolver o raciocínio matemático, pensamento computacional e por fim comunicar matematicamente. Este momento é construído para trabalhar diretamente com alunos, em oficina de turma, ou projeto, ou área disciplinar. |
SP 21 - Apps for Good - Giving young people the skills to shape their futureMatilde Buisel, CDI Portugal Terça-feira, 15 de julho, 14h00m - 16h00m Resumo O Apps for Good é um programa educativo inovador que desafia alunos a identificar problemas reais nas suas comunidades e a criar soluções tecnológicas com impacto. Seguindo uma metodologia de projeto assente no currículo, ao longo do percurso, os jovens desenvolvem competências digitais, pensamento crítico, criatividade e trabalho em equipa, tornando-se agentes de mudança. Mais do que utilizadores, tornam-se criadores de tecnologia, aprendendo a aplicá-la de forma responsável, ética e com um propósito. Notas biográficas Matilde Buisel - Mestre em Psicologia Clínica pela Universidade ISPA – Instituto Universitário de Ciências Psicológicas, Sociais e da Vida – em Lisboa. Fez o seu estágio em psicologia na clínica CADIN e é membro efetivo da Ordem dos Psicólogos. Trabalha no CDI Portugal como gestora de projeto do programa educativo tecnológico internacional Apps for Good. Fez um curso em Project Management em Nova Orleães com certificação pelo Project Management Institute (PMI) e participou num Bootcamp sobre impacto social e inovação, promovido pelo European Investment Bank Institute e Faculdade Católica de Lisboa. É também certificada em Competências Pedagógicas (CPP). No Apps for Good, tem gerido e acompanhado o arranque e a implementação do programa em Portugal desde o início. Paula Fernandes - Responsável de avaliação do impacto. Licenciada (pré-Bolonha) em Psicologia Clínica, na Variante Clínica e do Aconselhamento, pela ULHT de Lisboa e Pós-Graduada com Especialização em Terapias Comportamentais e Cognitivas, na APTCC. Orientadora de estágio profissional para a OPP. Atualmente é formadora de projetos no CDI Portugal e responsável pela avaliação do impacto. Sara Cordeiro - Gestora de Comunidades. Mestre em Psicologia da Saúde e Reabilitação Neuropsicológica, pela Universidade de Aveiro. Realizou estágios em contexto hospitalar e participou na organização da 10a edição das Jornadas da Psicologia enquanto Coordenação do Núcleo de Estudantes de Psicologia. |
SP 22 - A experimentação da Plataforma Mathigon no ensino de GeometriaLialda Bezerra Cavalcanti, Instituto Federal de Educação, Ciência e Tecnologia de Pernambuco / Unidade de Investigação e Desenvolvimento em Educação e Formação(UIDEF) Terça-feira, 15 de julho, 10h30m - 12h30m Resumo Os ambientes de geometria dinâmica permitem explorar objetos matemáticos de forma interativa no computador. Mediante a manipulação de figuras e a observação de propriedades em tempo real, os alunos são incentivados a formular conjeturas, justificar ideias nas situações-problema, e, assim desenvolver o raciocínio matemático. A plataforma Mathigon é um ambiente digital interativo com potencialidades para apoiar a aprendizagem da matemática, especialmente da geometria. Ao tornar visíveis relações abstratas por meio da exploração e da descoberta, auxiliar a compreensão de conceitos de geometria e apoia os alunos a superar dificuldades ligadas à abstração e à visualização. Nesta sessão prática, vamos explorar a plataforma Mathigon através de tarefas que estimulam o pensamento crítico e criativo dos alunos, mostrando como esta ferramenta didática pode apoiar o desenvolvimento de capacidades matemáticas essenciais e promover uma aprendizagem ativa e significativa. Nota: os participantes devem ser portadores de computores portáteis. Nota biográfica Lialda Bezerra Cavalcanti - Docente do Ensino Básico, Técnico e Tecnológico no Instituto Federal de Educação, Ciência e Tecnologia de Pernambuco (IFPE), Campus Recife da área de Matemática. Pós-doutoranda em Educação (Didática da Matemática) no Instituto de Educação da Universidade de Lisboa |
SP 23 - Resolução de problemas de Geometria e Funções com o GeoGebra: Representações múltiplasCristina Negra, Escola Básica e Secundária de Gama Barros Terça-feira, 15 de julho, 14h00m - 16h00m Resumo A “Resolução de problemas, modelação e conexões” (ID1), o “Recurso sistemático à tecnologia” (ID3) e as “Tarefas e recursos educativos” (ID4) são três das nove Ideias chave das Aprendizagens Essenciais (AE) para Matemática A. Notas biográficas Cristina Negra - Licenciada em Ensino de Matemática pela FCUL/UL. Formadora acreditada de professores. Elemento do Grupo de Trabalho do Desenvolvimento Curricular e Profissional em Matemática para o Ensino Secundário. Coautora dos projetos escolares Sem limites, Desafios e Dimensões. Colaboradora do projeto Estudo Em Casa e Estudo Em Casa Apoia. Emanuel Martinho - Licenciado em Ensino de Matemática pela UM. Mestre em Ensino de Matemática pela FCT/UNL. Formador acreditado de professores. Elemento do Grupo de Trabalho do Desenvolvimento Curricular e Profissional em Matemática para o Ensino Secundário. Coautor dos projetos escolares Sem limites, Desafios e Dimensões. Colaborador do projeto Estudo Em Casa e Estudo Em Casa Apoia. Pedro Pimenta - Licenciado em Matemática, ramo educacional, pela FCT/UNL. Mestre em Matemática para o Ensino pela FCUL. Doutorando em Educação (Inovação Educativa) na NOVA/ISPA. Formador acreditado de professores. Membro das comissões organizadoras do ProfNova e da ExpoFCT. Coautor dos projetos escolares Matemática a Giz de Cor, Sigma, Xis, Ípsilon, Novo Ípsilon, MatPower e Matemática 360. |
SP 24 - Pavimentações com ferramentas GeoGebraCarla Faneco, Agrupamento de Escolas de Sampaio Segunda-feira, 14 de julho, 14h30m - 16h30m Resumo O objetivo desta sessão prática é explorar potencialidades das ferramentas “Polígono”, “Polígono Regular” e “Polígono Rígido” do GeoGebra para a realização de tarefas que envolvem Pavimentações. Serão explorados vários guiões de tarefas: Utilização da ferramenta polígono regular com número de lados manipulável por seletor; Utilização da ferramenta polígono rígido para obter cópias dinâmicas; Construção de pavimentações com triângulos e com quadriláteros; Construção de pavimentações regulares e semirregulares. Nota: Para esta sessão prática, é necessário trazer um portátil. Notas biográficas Carla Faneco - Professora de Matemática do 2.º ciclo. Cristina Loureiro - Professora aposentada do ensino superior politécnico. Nuno Valério - Professor de Matemática do 2.º ciclo. |
SP 25 - MILAGE Aprender+ versão 2.0: Personalização, Autonomia e Inovação no Ensino da MatemáticaMauro Figueiredo, Universidade do Algarve Terça-feira, 15 de julho, 14h00m - 16h00m Resumo Nesta sessão prática será explorada a plataforma MILAGE Aprender+ 2.0, uma ferramenta digital portuguesa gratuita que promove a aprendizagem ativa e autónoma da Matemática através de dispositivos móveis ou computadores. Os participantes terão a oportunidade de experimentar a plataforma do ponto de vista do aluno e do professor, explorando as funcionalidades de correção automática, auto-avaliação, avaliação pelos pares, gamificação e personalização do percurso de aprendizagem. A sessão inclui também a apresentação de estratégias para integração da MILAGE no ensino presencial, bem como a criação e partilha de fichas de trabalho diferenciadas. Será ainda abordado o papel dos professores enquanto dinamizadores da plataforma e o reconhecimento através de prémios, rankings e moedas MILAGE. Pretende-se, assim, capacitar os docentes para uma utilização eficaz da MILAGE como ferramenta de apoio à aprendizagem e à motivação dos alunos. Nota biográfica Mauro Figueiredo - Professor da Universidade do Algarve, é o coordenador do projeto MILAGE Aprender+. Doutorado em Engenharia Informática, tem promovido a inovação no ensino da Matemática com recurso a tecnologias digitais, destacando-se na formação de professores e no desenvolvimento de conteúdos interativos. |
SP 26 - Recursos digitais e interativos para a Matemática no 3º Ciclo e Ensino SecundárioAssociação Atractor – Matemática Interactiva Segunda-feira, 14 de julho, 14h30m - 16h30m Resumo O objetivo desta sessão é explorar diversos conteúdos didáticos digitais (gratuitos) e interativos disponibilizados pelo Atractor para a aprendizagem da Matemática. NOTA: Os participantes desta sessão deverão ter computadores ou tablets com o programa GeCla instalado (que pode ser importado de https://www.atractor.pt/mat/GeCla/ ) Nota biográfica O Atractor é uma Associação sem fins lucrativos cujo objetivo principal é atrair para a Matemática. Atualmente disponibiliza uma ampla gama de recursos, muitos deles com um forte potencial para o Ensino da Matemática (www.atractor.pt). |
SP 27 - Ensinar a Programar através da MatemáticaAndreia Mordido, Faculdade de Ciências, Universidade de Lisboa Terça-feira, 15 de julho, 14h00m - 16h00m Resumo Esta sessão prática capacitará os professores de matemática dos ensinos básico e secundário de ferramentas básicas para promover a introdução dos estudantes à programação desde o 7o ano de escolaridade. Através de exemplos simples, enquadrados com o programa da matemática, faremos uma breve introdução à programação em Python, como recomendado nas aprendizagens essenciais no Ensino Secundário. Esta sessão prática tem como objetivo auxiliar na restruturação do ensino da matemática para incorporar a introdução do pensamento computacional, através de uma fusão de conceitos de matemática e de programação. Nota: Os participantes na sessão prática deverão ter computador portátil com acesso à internet. Nota biográfica Andreia Mordido - Professora Auxiliar do Departamento de Informática da Faculdade de Ciências da Universidade de Lisboa, onde leciona desde 2018. Em 2009 licenciou-se em Matemática pela Faculdade de Ciências e Tecnologia da Universidade Nova de Lisboa, em 2011 fez o Mestrado em Matemática e Aplicações pelo Instituto Superior Técnico da Universidade de Lisboa e em 2017 fez o doutoramento em Segurança de Informação pela Universidade de Lisboa. |
SP 28 - Matemática: caminhos traçados pela curiosidade.Beatriz Barradas David, Universidade de Évora Terça-feira, 15 de julho, 10h30m - 12h30m Resumo Esta sessão prática propõe uma imersão no universo da matemática através de tarefas que despertam a curiosidade, promovem o pensamento crítico e valorizam a construção do conhecimento em grupo. Partindo da premissa de que a aprendizagem matemática se enriquece quando nasce da exploração e da descoberta, os participantes serão convidados a experimentar propostas que cruzam raciocínio, criatividade e contexto real. Nota: Os participantes na sessão prática deverão ter computador portátil com acesso à internet. Nota biográfica Beatriz Barradas David - Natural de Sintra, nascida a 19 de setembro de 2002. Frequência do ensino secundário na escola de Santa Maria, em Sintra, na área de línguas e humanidades. Em 2020, ingresso na licenciatura em Educação Básica, na Universidade de Évora com conclusão em 2023, tendo ingressado no mesmo ano no Mestrado em Educação Pré-Escolar e Ensino do 1.º Ciclo do Ensino Básico, na mesma instituição. |
SP 29 - O processo de ensino e aprendizagem da Combinatória: uma experiência de ensinoMónica Valadão, Escola Básica e Secundária Tomás de Borba, Terceira, Açores Terça-feira, 15 de julho, 14h00m - 16h00m Resumo A Análise Combinatória é um tema de grande potencial como contexto para a resolução de problemas, bem como pela aplicação em outras áreas do conhecimento. Nota: Os participantes na sessão prática deverão ter computador portátil com acesso à internet. Notas biográficas Mónica Valadão - Professora de Matemática no 3.º ciclo do Ensino Básico e Ensino Secundário, na Ilha Terceira, Açores. Doutoranda em Didática da Matemática no Instituto de Educação da Universidade de Lisboa. Fez parte da equipa de formação e acompanhamento dos professores de matemática do ensino básico, na Região Autónoma dos Açores. No triénio de 2022/2025 foi membro da direção da APM. Nélia Amado - Doutora em Matemática, especialidade de Didática da Matemática, pela Universidade do Algarve. É professora auxiliar da Faculdade de Ciências e Tecnologia da Universidade do Algarve e membro do Centro de Investigação e Desenvolvimento em Matemática e Aplicações – CIDMA. Colaboradora externa do Programa de Pós-Graduação em Ensino da Universidade do Vale do Taquari – UNIVATES, no Brasil. |
ProfMat 2025 - Simpósios de Comunicações (1h)
Os simpósios são espaços para a apresentação de comunicações (15 minutos cada), que divulgam experiências, projetos, trabalhos, investigações ou outras intervenções com relevância na Educação Matemática. Têm uma duração global que permite a apresentação das comunicações e um tempo de discussão, para que a audiência possa formular questões, no final das apresentações.
Simpósio de Comunicações 01 (SC 01)
Inteligência Artificial e Machine Learning
Segunda-feira, 14 de julho, 15h30 - 16h30
Sala 115
Moderador: Alcino Simões
| A |
Chat GPT obtém 18.8 valores no exame nacional de Matemática A (Resumo) Sandra Gaspar Couto, Instituto Superior de Engenharia de Lisboa Público: Geral |
| B |
Uma experiência crítica com a IA na resolução de exercícios de Matemática (Resumo) M.ª Cristina Costa, Instituto Politécnico de Tomar Público: 3.º ciclo e Secundário |
| C |
Dissertação “Utilização de técnicas de Machine Learning no processo de ensino-aprendizagem” (Resumo) Cristina Barbosa, Agrupamento de Escolas de Sines Público: Geral |
Simpósio de Comunicações 02 (SC 02)
Pensamento Computacional
Segunda-feira, 14 de julho, 15h30 - 16h30
Sala 295
Moderador: Manuel Vara Pires
| A |
Reconhecimento de Padrões e Pensamento Computacional no 1.º Ciclo: Uma Abordagem Didática em Contexto de Estágio (Resumo) Deolinda Silva, Escola Superior de Educação de Bragança – Instituto Politécnico de Bragança Público: 1.º ciclo |
| B |
Matemática em Movimento: Pensamento Computacional e Estatística em Contexto Escolar (Resumo) Marcela de Seabra, Escola Superior de Educação de Bragança – Instituto Politécnico de Bragança Público: 3.º ciclo |
| C |
Matemática e Pensamento Computacional com Python (Resumo) Dora Azevedo, Agrupamento de Escolas Nuno de Santa Maria Público: 3.º ciclo e Secundário |
Simpósio de Comunicações 03 (SC 03)
Conexões em Matemática
Segunda-feira, 14 de julho, 15h30 - 16h30
Sala 298
Moderadora: Paula Teixeira
| A |
Arte e Ciência (Resumo) Helena Paula Castro, Agrupamento Escolas Fernando Namora, Amadora Público: Secundário |
| B |
Projetos STEAM e avaliação: ideias e práticas (Resumo) Cristina Martins, Escola Superior de Educação e Centro de Investigação Transdisciplinar em Educação e Desenvolvimento, Instituto Politécnico de Bragança Público: 3.º ciclo e Secundário |
| C |
Matemática na rua. Uma atividade para a popularização da matemática. (Resumo) Onofre Monzó del Olmo, Federación Española de Sociedades de Profesores de Matemáticas (FESPM) Público: Geral |
Simpósio de Comunicações 04 (SC 04)
História da Matemática
Terça-feira, 15 de julho, 12h00 - 13h00
Sala 295
Moderadora: Alexandra Sofia Rodrigues
| A |
Matemática Recreativa Hoje (Resumo) Maria Teresa Serrão Sanches Gonçalves, Escola Básica e Secundária Ribeiro Sanches Público: 3.º cilo e Secundário |
| B |
A Matemática Moderna nas Escolas Industriais: Uma Análise Histórica de Currículos e Intenções (Resumo) Verónica Pereira, Instituto Politécnico de Viseu - ESTGL & Centro Interdisciplinar de Ciências Sociais (CICS.NOVA) Público: Geral |
| C |
Material Didático em Geometria na formação de professores: Uma pincelada sobre o período 1986 a 2006 (Resumo) Ana Santiago, Escola Superior de Educação-Instituto Politécnico de Coimbra Público: Geral |
Simpósio de Comunicações 05 (SC 05)
Calculadora Gráfica
Terça-feira, 15 de julho, 12h00 - 13h00
Anfiteatro 131
Moderador: Joaquim Rosa
| A |
Modelação do movimento com tecnologia gráfica: do lançamento à análise de dados (Resumo) Ana Rita Reis, Universidade Nova de Lisboa - Faculdade de Ciências e Tecnologias Público: Secundário |
| B |
A calculadora gráfica na conexão entre a Geometria e as Funções com o contributo da Mediação Semiótica (Resumo) Manuela Subtil, Agrupamento de Escolas Fragata do Tejo, Escola Superior de Educação de Lisboa, CICS.NOVA Público: 3.º ciclo e Secundário |
Simpósio de Comunicações 06 (SC 06)
Inclusão e diferenciação pedagógica
Terça-feira, 15 de julho, 12h00 - 13h00
Sala 298
Moderador: Ricardo Vicente
| A |
Ensino da Matemática para alunos com perturbação do espectro do autismo (Resumo) Corália Pimenta, Agrupamento de Escolas Coimbra Centro Público: 1.º ciclo |
| B |
Educação Matemática Inclusiva: o caminho para uma Matemática de excelência para todos (Resumo) Ricardo Machado Vicente, Agrupamento de Escolas de Perafita, Matosinhos Público: Geral |
| C |
A Diferenciação Pedagógica na aula de Matemática, um exemplo de como “+ com + dá -” (Resumo) Ana Sofia Cartaxo Pinheiro Pereira, Colégio Académico | CeiED Universidade Lusófona de Lisboa Público: 2.º ciclo |
Simpósio de Comunicações 07 (SC 07)
Desenvolvimento curricular
Quarta-feira, 16 de julho, 9h00 - 10h00
Sala 110
Moderadora: Renata Carvalho
| A |
Construindo aprendizagens essenciais de matemática no 4.º ano em interlocução coletiva (Resumo) Helena Gil Guerreiro, AE Braamcamp Freire Público: 1.º ciclo |
| B |
Analisando conexões estabelecidas por alunos do ensino básico na resolução de tarefas (Resumo) Catarina Fonseca, Escola Superior de Educação, Instituto Politécnico de Bragança Público: Ensino Básico |
| C |
Um manual escolar que conta uma história. O ensino da geometria. (Resumo) Alexandra Sofia Rodrigues, EDUNOVA.ISPA Centro de Investigação Interdisciplinar em Educação; CICS.NOVA Centro Interdisciplinar de Ciências Sociais; Faculdade de Ciências e Tecnologia da Universidade NOVA de Lisboa, UIED Público: 3.º ciclo |
Simpósio de Comunicações 08 (SC 08)
Formação de professores
Quarta-feira, 16 de julho, 9h00 - 10h00
Sala 115
Moderadora: Nadia Ferreira
| A |
Formação de Professores em Ensino de Matemática com recurso à Tecnologia – Do Currículo Prescrito ao Currículo em Ação (Resumo) Pedro Pimenta, Escola Básica e Secundária do Monte de Caparica Público: Geral |
| B |
Exposição Geometria Inquieta: uma experiência em um espaço não-formal durante um curso de formação continuada para professores (Resumo) Marcelo de Oliveira Dias, Universidade Federal Rural do Rio de Janeiro (UFRRJ) Público: Secundário |
Simpósio de Comunicações 09 (SC 09)
Metodologias inovadoras
Quarta-feira, 16 de julho, 9h00 - 10h00
Sala 296
Moderador: Emanuel Martinho
| A |
Trabalho de Projeto “Notitia Mathesis: noticiário criativo de aprendizagem matemática” (Resumo) Eduardo Cunha, Agrupamento de Escolas de Barcelos Público: Secundário |
| B |
Problema de Fermi no âmbito das comemorações do 25 de abril de 1974 por alunos do 5.º ano de escolaridade (Resumo) Manuela Subtil, Agrupamento de Escolas Fragata do Tejo, Escola Superior de Educação de Lisboa, CICS.NOVA Público: 2.º ciclo |
| C |
Portefólios Digitais na Disciplina de Matemática (Resumo) Filipa Susana da Graça Ferreira, AE Maria do Carmo Serrote, Sesimbra Público: 3.º ciclo |
RESUMOS
SC 01 | A Chat GPT obtém 18.8 valores no exame nacional de Matemática ASandra Gaspar Couto | Universidade Nova de Lisboa Segunda-feira, 14 de julho, 15h30m - 16h30m Resumo A inteligência artificial (IA) está progressivamente a integrar-se no nosso quotidiano. Considerava-se que disciplinas de natureza formal e rigorosa, como a Matemática, estariam fora do seu alcance, dado que a IA assenta num modelo probabilístico de linguagem, mas os avanços recentes desafiam essa suposição. Neste estudo, solicitámos ao ChatGPT-4 que resolvesse o exame nacional de Matemática A (1.ª fase, 2024). Foi classificado seguindo os critérios de correção do IAVE obtendo uma classificação de 18,8 valores. Este resultado levanta questões relevantes sobre o potencial da IA como ferramenta de apoio à aprendizagem, nomeadamente no ensino secundário. Poderá o ChatGPT constituir um recurso pedagógico eficaz no estudo autónomo da Matemática? A possibilidade de solicitar explicações adicionais, validar procedimentos ou esclarecer dúvidas em tempo real torna esta ferramenta particularmente apelativa. Este estudo convida à reflexão sobre o papel emergente da IA na educação matemática. Notas biográficas Sandra Gaspar Couto - Docente de matemática do Instituto Superior de Engenharia de Lisboa desde 2000. Foi docente do ensino básico durante 3 anos. É doutorada em Ciências da Educação pela Universidade Nova de Lisboa. Um grande foco do seu trabalho é tirar partido da tecnologia para fomentar a aprendizagem significativa dos alunos. |
SC 01 | B Uma experiência crítica com a IA na resolução de exercícios de MatemáticaM.ª Cristina Costa | Instituto Politécnico de Tomar Segunda-feira, 14 de julho, 15h30m - 16h30m Resumo Numa era cada vez mais tecnológica, dominada pela presença da Inteligência Artificial (IA) e pela sua crescente utilização, é fundamental ter uma visão crítica sobre as vantagens e desvantagens das ferramentas de IA atualmente disponíveis. Desta forma, não só se torna crucial repensar a forma de ensinar, mas também é necessário encontrar novas formas de avaliar os estudantes. Notas biográficas M.ª Cristina Costa - Licenciatura, mestrado, e curso de Doutoramento em Matemática. É Doutoradaem Ciências da Educação e tem Pós-doc em educação STEAM, pela FCT da Universidade NOVA de Lisboa. Desde 2013 que é diretora da Academia de Ciência, Arte e Património www.academiacap.ipt.pt), tendo sido responsável pela submissão e coordenação de várias oficinas acreditadas relacionadas com as STEAM e Pensamento Computacional, destinadas a professores desde o ensino básico ao secundário. |
SC 01 | C Dissertação “Utilização de técnicas de Machine Learning no processo de ensino-aprendizagem”Cristina Barbosa | Agrupamento de Escolas de Sines Segunda-feira, 14 de julho, 15h30m - 16h30m Resumo A presente comunicação tem por base a divulgação do trabalho de dissertação “Utilização de técnicas de machine learning no processo de ensino-aprendizagem” do Mestrado Matemática para Professores em 2023, na Universidade de Aveiro. O trabalho propõe-se definir e divulgar a utilização das técnicas de machine learning (ramo da inteligência artificial) na educação, de modo particular, dentro da área da matemática. A dissertação é composta por um perfil teórico das principais ideias e fontes de conhecimentos destas áreas, com propostas de aplicações atuais nas plataformas Orange Data Mining e Google Colab, com uso da linguagem de programação Python. Torna-se uma evidência que os "camarins" da matemática, informática aplicada e processos de ensino aprendizagem são essenciais às revoluções tecnológicas a que assistimos no mundo. Nota biográfica Cristina da Conceição Barbosa - Mestre e professora de Matemática do 3.º Ciclo (Grupo 500) no Agrupamento de Escolas de Sines. Fez a sua formação inicial com a licenciatura pré-Bolonha em Matemáticas Aplicadas (ramo formação educacional) na Universidade Lusíada do Porto. Realizou 4 cadeiras do Mestrado em Informática Aplicada na ESTGA – Escola Superior de Tecnologia e Gestão de Águeda da Universidade de Aveiro. Em 2023 concluiu o mestrado em Matemática para Professores na Universidade de Aveiro. Ao longo da sua vida foi fazendo formação nas diversas áreas dedicadas. Deu apoio ao estudo, explicações de matemática e colaborou com empresas de Indústria e Serviços como a Modelo Continente, Galp Energia e Lactogal antes de iniciar o seu percurso de coadjuvante e titular da disciplina de matemática do 3.º Ciclo do Ensino Básico, nos últimos anos. |
SC 02 | A Reconhecimento de Padrões e Pensamento Computacional no 1.º Ciclo: Uma Abordagem Didática em Contexto de EstágioDeolinda Silva | Escola Superior de Educação de Bragança – Instituto Politécnico de Bragança Segunda-feira, 14 de julho, 15h30m - 16h30m Resumo Este estudo, desenvolvido no âmbito do estágio de uma aluna de mestrado em ensino, investiga como o reconhecimento de padrões pode ser promovido no 1.º ano do 1.º ciclo do ensino básico, numa abordagem didática integrada ao pensamento computacional. Através de sequências visuais, jogos e tarefas exploratórias, os alunos foram desafiados a identificar regularidades e formular generalizações. Os resultados evidenciam que estratégias didáticas bem orientadas potenciam o raciocínio lógico desde os primeiros anos de escolaridade. Nota biográfica Marcela Seabra - Doutoranda em Educação na FCT NOVA e Bolseira da FCT. Professora convidada na ESE de Bragança desde 2009 e integra o Centro de Investigação Transdisciplinar em Educação e Desenvolvimento. A área de investigação recai na formação de professores, tecnologia educativa, inovação no ensino da matemática e pensamento computacional. Possui mestrado em Tecnologia Educativa e licenciatura em Matemática Ensino pela Universidade do Minho. |
SC 02 | B Matemática em Movimento: Pensamento Computacional e Estatística em Contexto EscolarMarcela de Seabra | Escola Superior de Educação de Bragança – Instituto Politécnico de Bragança Segunda-feira, 14 de julho, 15h30m - 16h30m Resumo Este estudo apresenta uma experiência pedagógica com alunos do 7.º ano que integra pensamento computacional no ensino da estatística. Através da atividade "Matemática em Movimento", os alunos exploraram espaços escolares recolhendo dados reais para calcular média, moda, mediana e probabilidades. A metodologia promove decomposição de problemas, reconhecimento de padrões e abstração, desenvolvendo literacia estatística e competências digitais. Nota biográfica Marcela Seabra - Doutoranda em Educação na FCT NOVA e Bolseira da FCT. Professora convidada na ESE de Bragança desde 2009 e integra o Centro de Investigação Transdisciplinar em Educação e Desenvolvimento. A área de investigação recai na formação de professores, tecnologia educativa, inovação no ensino da matemática e pensamento computacional. Possui mestrado em Tecnologia Educativa e licenciatura em Matemática Ensino pela Universidade do Minho. |
SC 02 | C Matemática e Pensamento Computacional com PythonDora Azevedo | Agrupamento de Escolas Nuno de Santa Maria Segunda-feira, 14 de julho, 15h30m - 16h30m Resumo O Pensamento Computacional e a Programação, nomeadamente na linguagem Python têm vindo a ganhar relevância no currículo do sistema educativo, em particular nas Aprendizagens Essenciais de Matemática. Estas referem que o pensamento computacional favorece o desenvolvimento, de forma integrada, de práticas como a abstração, a decomposição, o reconhecimento de padrões, a análise e definição de algoritmos e o raciocínio. Estas práticas são imprescindíveis no ensino da Matemática e fornecem aos alunos ferramentas que lhes permitem resolver problemas, em especial relacionados com a programação. Neste sentido, apresentamos uma atividade no âmbito da Autonomia e Flexibilidade Curricular, que desenvolvemos com alunos do 9.º ano e 10.º ano de escolaridade, onde abordámos a resolução de equações do 2.º grau e estudo da função quadrática, com recurso à linguagem de programação Python. Notas biográficas Dora Isabel Oliveira Freitas Azevedo - Licenciada em Matemática (Via ensino), da Faculdade de Ciências da universidade de Lisboa. Frequência do Curso Gestão de Empresas, no IPT. Microcredenciações: Matemática e Pensamento Computacional com Python e Análise Exploratória de Dados com Software Estatístico; docente do grupo 500, no AENSM mas QA do AEO, em Ourém. |
SC 03 | A Arte e CiênciaHelena Paula Castro | Agrupamento Escolas Fernando Namora, Amadora Segunda-feira, 14 de julho, 15h30m - 16h30m Resumo Arte e Ciência, projeto em desenvolvimento desde 2020 e já na sua 4.a edição, ganha formas diferentes em cada ano letivo. E se o trabalho de «projeto» era, até agora, só uma opção pedagógica de alguns professores, neste momento é um «tópico» previsto no novo programa de Matemática A (10.o ano), o que vem reconhecer a importância do trabalho que se tem vindo a desenvolver e dos seus princípios orientadores, um dos quais dá nome ao projeto: o encontro da Arte e das Ciências. Nota biográfica Helena Castro - Licenciatura pré Bolonha em Ensino da Matemática, pela Fac. de Ciências de Lisboa (1997), Pós-Graduação em Novas Tecnologias Aplicadas à Educação e Formação, pelo Instituto Superior de Educação e Ciências, (2008) e doutoranda em Didática da Matemática, pelo Instituto de Educação. Professora do grupo 500 desde 1988. Em 1997, entrou no Agrupamento de Escolas Fernando Namora, Amadora, onde tem desempenhado diversos cargos, nomeadamente nas equipas STEAM e PADDE e Coordenadora de Projetos, entre outros. |
SC 03 | B Projetos STEAM e avaliação: ideias e práticasCristina Martins | Escola Superior de Educação e Centro de Investigação Transdisciplinar em Educação e Desenvolvimento, Instituto Politécnico de Bragança Segunda-feira, 14 de julho, 15h30m - 16h30m Resumo O Processo de Bolonha evidenciou a valorização de um modelo de formação, no ensino superior, centrado em competências. Neste contexto, destaca-se a importância de práticas integradoras, como a abordagem STEAM e a avaliação pedagógica na promoção da aprendizagem autónoma dos estudantes. Esta comunicação resulta de uma investigação sustentada numa revisão sistemática da literatura (RSL), orientada pela questão: Que conceitos e práticas articulam projetos STEAM e avaliação na formação inicial de professores (FIP)? A RSL evidencia a escassez de estudos que explicitem práticas avaliativas em projetos STEAM. Decorre daqui a proposta de sugestões e experiências que superem a fragmentação curricular e o foco na avaliação sumativa, promovendo práticas integradas e formativas. Estas devem sensibilizar os formadores para a melhoria da FIP, favorecendo aprendizagens significativas e contribuindo para o desenvolvimento da futura prática docente. Notas biográficas Cristina Martins - Docente da Escola Superior de Educação do Instituto Politécnico de Bragança. Doutora em Educação, Especialidade Didática da Matemática, com uma tese centrada no desenvolvimento profissional de professores de 1.º CEB. Do seu curriculum vitae destaca a docência na formação inicial de educadores e professores; a ligação à formação contínua de professores como formadora (nomeadamente do Programa de Formação Contínua em Matemática (2005-2010) e coordenadora do gabinete de formação contínua da ESE de Bragança durante 10 anos. Integra vários projetos de investigação. Participou num projeto piloto com e para professores do 1.ºCEB e educadores de infância centrado no sucesso escolar; coordenou um estudo sobre crenças, saberes e práticas de professores e integrou o Grupo de Trabalho de Desenvolvimento Curricular e Profissional em Matemática. |
SC 03 | C Matemática na rua. Uma atividade para a popularização da matemática.Onofre Monzó del Olmo | Federación Española de Sociedades de Profesores de Matemáticas (FESPM) Segunda-feira, 14 de julho, 15h30m - 16h30m Resumo A Federação Espanhola das Sociedades de Matemática (FESPM) coordena e incentiva as suas sociedades associadas a realizar a atividade “Matemática na Rua”. Como professores de matemática, muitas vezes concentramo-nos em mais do que apenas a educação matemática dos nossos alunos. Esforçamo-nos também por demonstrar a importância da nossa área e a sua presença na vida quotidiana da nossa sociedade. A Matemática na Rua é uma atividade que pretende levar a matemática a todos os públicos fora do ambiente escolar, como o próprio nome sugere, na rua, de uma forma lúdica e informativa, oferecendo atividades adaptadas a vários níveis. Trata-se de mostrar a matemática de uma forma prazerosa. As ideias matemáticas podem ser apresentadas de uma forma mais natural e acessível. Vamos apresentar como se organiza esta atividade e algumas das atividades que são realizadas. Nota biográfica Onofre Monzó del Olmo - Professor de matemática no ensino secundário, participei como investigador em quatro projetos de I+D+I, publiquei livros e artigos sobre o ensino e a aprendizagem da matemática e editei a revista SUMA. Participei como orador em vários congressos e workshops sobre o ensino e aprendizagem da matemática. Desde 2006 que sou presidente da Sociedade de Educação Matemática da Comunidade Valenciana “al-Khwārizmī” (SEMCV) e do Instituto Valenciano de Geogebra (IGV). E de 2013 a 2022 fui presidente da Federação Espanhola das Sociedades de Professores de Matemática (FESPM), e desde 2022 sou o seu vice-presidente. |
SC 04 | A Matemática Recreativa HojeMaria Teresa Serrão Sanches Gonçalves | Escola Básica e Secundária Ribeiro Sanches Terça-feira, 15 de julho, 12h00m - 13h00m Resumo Sustentada em trabalho investigativo já desenvolvido e na reflexão sobre a prática educativa em espaços informais, esta comunicação pretende apresentar algumas ideias que sirvam de base para discussão e troca de perspectivas. Pretendemos “entrar” num Clube de Matemática, propor de forma recreativa a exploração de uma atividade orientada e criar uma oportunidade pedagógica que permita a exploração de aprendizagens e por conseguinte, a compreensão mais concreta e experienciada de conceitos que, em geral, permanecem apenas no domínio teórico. Nota biográfica Maria Teresa S. Sanches G. - Licenciada em Ensino de Matemática e doutorou-se em Didática da Matemática pela Universidade da Beira Interior. Exerce funções docentes na EB e Secundária Ribeiro Sanches. Integra o Grupo de Trabalho sobre História e Memórias do Ensino da Matemática da Associação de Professores de Matemática (GTHMEM). Os seus principais interesses de investigação prendem-se com questões ligadas à Didática da Geometria, especificamente as metodologias no ensino (aprendizagem) da Geometria e à Geometria na História da Educação Matemática. |
[Início_SC]
SC 04 | B A Matemática Moderna nas Escolas Industriais: Uma Análise Histórica de Currículos e IntençõesVerónica Pereira | Instituto Politécnico de Viseu - ESTGL & Centro Interdisciplinar de Ciências Sociais (CICS.NOVA) Terça-feira, 15 de julho, 12h00m - 13h00m Resumo O conhecimento do percurso histórico de uma disciplina leva-nos a analisar melhor as questões da época e a refletir, com mais consciência, sobre as nossas futuras escolhas educativas. Nesta comunicação apresentaremos uma análise histórica da introdução da Matemática Moderna (MM) na disciplina de Matemática nos cursos técnicos industriais portugueses na década de 1960 e a sua posterior generalização. No contexto de uma ampla internacionalização da reforma curricular e à luz do seminário de Royaumont, o movimento procurou alinhar o ensino aos avanços da MM e ao desafio de uma sociedade em transformação tecnológica. Com base em programas oficiais e outras fontes documentais, a evolução da introdução da MM nas escolas técnicas será traçada e revelada com os seus objetivos, currículo e as mudanças. Sendo fornecida uma cronologia dos movimentos matemáticos mundiais e nacionais, com destaque para a MM no panorama educativo. Esta abordagem histórica permite-nos recuperar memórias perdidas e abrir novas linhas de reflexão sobre um dos momentos mais decisivos da história da reforma do ensino da matemática em Portugal. Notas biográficas Verónica Pereira - Doutorada em Didática da Matemática. Sua investigação centra-se na avaliação de competências matemáticas, com destaque para a aplicação da Taxonomia SOLO na análise da aprendizagem de estudantes. Tem desenvolvido estudos comparativos sobre avaliação presencial e online, bem como pesquisas sobre a experiência de ensino e aprendizagem do ponto de vista de professores e alunos e atividades STEM no ensino básico/superior. Participa ativamente em projetos colaborativos com investigadores de instituições como a Universidade Nova de Lisboa e o Instituto Politécnico de Coimbra. |
[Início_SC]
SC 04 | C Material Didático em Geometria na formação de professores: Uma pincelada sobre o período 1986 a 2006Ana Santiago | Escola Superior de Educação-Instituto Politécnico de Coimbra Terça-feira, 15 de julho, 12h00m - 13h00m Resumo Considerando que o estudo do passado, pode ajudar à compreensão dos problemas do ensino e da aprendizagem da matemática atual (Matos, 2020), pareceu-nos importante examinar perspetivas de utilização do material didático em Geometria, fomentadas na formação de professores do 1.º Ciclo do Ensino Básico, entre 1986 e 2006. Este trabalho tem por meta compreender e caracterizar o desenvolvimento de Educação Matemática naquele contexto e como objetivo imediato identificar o material disponível bem como auscultar a metodologia adequada para que a meta possa ser alcançada. |
[Início_SC]
SC 05 | A Modelação do movimento com tecnologia gráfica: do lançamento à análise de dadosAna Rita Reis | Faculdade de Ciências e Tecnologias Terça-feira, 15 de julho, 12h00m - 13h00m Resumo As tarefas a apresentar foram desenvolvidas na disciplina de Modelação e Aplicações no Ensino da Matemática, no Mestrado em Ensino da Matemática da NOVA-FCT. Sob o mote dos "jogos interturmas", surgiram dois desafios: o Grande Torneio da Catapulta e o Torneio da Bola Saltitona. A primeira tarefa usa o menu Picture Plot da calculadora Casio para analisar o movimento de uma bola lançada por uma catapulta, permitindo explorar modelos de funções quadráticas. A segunda baseia-se em dados recolhidos com o sensor de movimento, usando calculadoras TI-Nspire, para estudar o comportamento de bolas saltitonas, através de gráficos e funções por ramos. Ambas integram tecnologia no processo de aprendizagem, promovendo a experimentação e a ligação da Matemática a situações reais. Este tipo de tarefa desperta nos alunos a necessidade de atingirem um objetivo concreto, tornando a aprendizagem da matemática orientada para a resolução de problemas reais. Notas biográficas Sara Domingos - Aluna do 1.º ano do Mestrado em Ensino da Matemática da NOVA-FCT. Concluiu, em 2023, a licenciatura em Matemática Aplicada à Economia e à Gestão pela Universidade do Algarve. No ano letivo 2023/2024, lecionou Matemática no Agrupamento de Escolas D. Manuel I, em Tavira. |
[Início_SC]
SC 05 | B A calculadora gráfica na conexão entre a Geometria e as Funções com o contributo da Mediação SemióticaManuela Subtil | Agrupamento de Escolas Fragata do Tejo, Escola Superior de Educação de Lisboa, CICS.NOVA Terça-feira, 15 de julho, 12h00m - 13h00m Resumo Esta comunicação apoia-se nos construtos teóricos da génese instrumental e visa analisar a resolução de uma tarefa no 7.o ano de escolaridade, de índole exploratória, com recurso ao artefacto mediador, calculadora gráfica, onde se pretendeu fazer uma conexão entre os domínios de Geometria e Funções. Procurou-se compreender como é que emergiram signos de artefacto através do desenvolvimento de esquemas de uso e esquemas de ação instrumentada, e posteriormente como é que se deu a transição para signos matemáticos. Notas biográficas Manuela Subtil - Professora de Matemática do grupo 500 e professora adjunta convidada do domínio científico de Matemática. É Licenciada e Mestre em Ensino de Matemática no 3.o Ciclo e Ensino Secundário e Doutora em Ciências da Educação. É autora de livros escolares e artigos publicados em revistas. Também tem publicados, posters e comunicações, em atas de congressos nacionais e internacionais. Tem participado em alguns projetos, sendo investigadora colaboradora do CICS.NOVA e UIED. |
[Início_SC]
SC 06 | A Ensino da Matemática para alunos com perturbação do espectro do autismoCorália Pimenta | Agrupamento de Escolas Coimbra Centro Terça-feira, 15 de julho, 12h00m - 13h00m Resumo A educação inclusiva, conforme preconizado no Decreto-Lei n.o 54/2018, assenta no princípio da equidade e na valorização da diversidade como oportunidade de enriquecimento para todos. Nesse âmbito, todos os alunos, incluindo os com Perturbação do Espectro do Autismo (PEA), devem aceder a uma aprendizagem de qualidade, com pleno envolvimento no processo educativo. No ensino da Matemática, aqueles alunos podem apresentar dificuldades específicas, como a abstração, exigindo aos docentes um esforço acrescido de diferenciação pedagógica e flexibilização curricular. Torna-se essencial o recurso a metodologias variadas, materiais visuais, tarefas estruturadas e tecnologias digitais que favoreçam o desenvolvimento das competências definidas no Perfil dos Alunos à Saída da Escolaridade Obrigatória. Este trabalho partilha o acompanhamento de um aluno do 1.o ciclo ao longo de quatro anos, dando visibilidade às dificuldades sentidas, aos avanços registados e às estratégias implementadas. Sublinham-se a importância da colaboração docente e a criação de ambientes de aprendizagem inclusivos, flexíveis e centrados nas necessidades e potencialidades do aluno. Notas biográficas Corália Pimenta - Docente no Agrupamento de Escolas Coimbra Centro e professora convidada no Instituto Politécnico de Coimbra. É licenciada em Matemática – ramo educacional pela Faculdade de Ciências e Tecnologia de Coimbra, tem especialização em Educação Especial, pela Escola de Educação de Coimbra, é Mestre em Ensino da Matemática – 3o ciclo e secundário e Doutorada em Didática da Matemática pela Universidade da Beira Interior. A sua área de investigação centra-se na construção do conhecimento da Matemática, também com foco nas dificuldades de aprendizagem. |
[Início_SC]
SC 06 | B Educação Matemática Inclusiva: o caminho para uma Matemática de excelência para todosRicardo Machado Vicente | Agrupamento de Escolas de Perafita, Matosinhos Terça-feira, 15 de julho, 12h00m - 13h00m Resumo Ainda pouco desenvolvida em Portugal, a Educação Matemática Inclusiva é um domínio da Educação Matemática centrado nas práticas de ensino-aprendizagem-avaliação da disciplina e nos conceitos de equidade, diferenciação e inclusão. Nota biográfica Ricardo Machado Vicente - Docente de Matemática e Ciências Naturais no Agrupamento de Escolas de Perafita – Matosinhos; mestre em Administração e Organização Educacional; especializado em Educação Especial - domínio cognitivo e motor e domínio da visão e doutorando em Educação. A sua investigação doutoral centra-se na relação entre as áreas da Educação Matemática e da Educação Inclusiva, e na forma como ambas podem, em articulação, contribuir para que todos os alunos aprendam uma Matemática de excelência. |
[Início_SC]
SC 06 | C A Diferenciação Pedagógica na aula de Matemática, um exemplo de como “+ com + dá -”Ana Sofia Cartaxo Pinheiro Pereira | Colégio Académico | CeiED Universidade Lusófona de Lisboa Terça-feira, 15 de julho, 12h00m - 13h00m Resumo A diferenciação pedagógica é uma abordagem essencial para tornar o ensino à medida (Tomlinson, 2014) e é importante que integre todos os meios tecnológicos, mas que não se desfaça de estratégias com manipuláveis, especialmente na Matemática, tendo em vista uma aprendizagem significativa. Nota biográfica Ana Sofia Pereira - Licenciada em Matemática e Ciências da Computação, com curso de mestrado em Matemática para o Ensino, pela Universidade de Évora. Doutoranda em Educação, integra a comunidade de investigação de Aprendizagem e Inovação do CeiED da Universidade Lusófona de Lisboa. É especialista em Educação Especial e Educação Inclusiva. É Professora e Coordenadora da EMAEI no Colégio Académico. A sua área de investigação é a Educação Matemática, com particular interesse na Diferenciação Pedagógica e Modelos Educativos. Com formação em Coaching Educativo e Sucesso Escolar, é autora do projeto @matematicacoach que procura valorizar a aprendizagem e promover o espírito crítico, a autonomia e resiliência, relativamente à Matemática. É também co-autora do projeto @ed.minds que ambiciona promover uma educação inclusiva, empática e humanizada. |
[Início_SC]
SC 07 | A Construindo aprendizagens essenciais de matemática no 4.º ano em interlocução coletivaHelena Gil Guerreiro | AE Braamcamp Freire Quarta-feira, 16 de julho, 9h00m - 10h00m Resumo No ano da publicação da brochura “Capacidades matemáticas transversais no 1.° Ciclo do Ensino Básico - 3.° e 4.° anos” vamos partilhar episódios de momentos coletivos da exploração e discussão de tarefas que dela fazem parte, que envolveram uma das turmas da operacionalização antecipada do 4.º ano, durante o ano letivo de 2022/2023. Pretendemos dar a conhecer como tarefas desafiantes podem contribuir para uma aprendizagem matemática que integra os três princípios das aprendizagens essenciais. Através de um trabalho cooperativo e em interlocução coletiva foi possível implicar os alunos no processo de aprendizagem, permitindo-lhe que discutissem entre si as suas produções matemática, construindo e sistematizando, coletivamente, as aprendizagens matemáticas previstas. Notas biográficas Helena Gil Guerreiro - Doutorada em Educação, na área de especialidade de Didática da Matemática pelo Instituto de Educação da Universidade de Lisboa, mestre na área de especialidade da Didática da Matemática, e licenciada em Ensino Básico, variante Matemática/Ciências da Natureza pela Escola Superior de Educação de Lisboa. É professora no 1.º Ciclo no Agrupamento de Escolas Braamcamp Freire e professora adjunta convidada na Escola Superior de Educação de Lisboa. Integra o grupo de Trabalho do Desenvolvimento Curricular e Profissional em Matemática (DCPM). |
[Início_SC]
SC 07 | B Analisando conexões estabelecidas por alunos do ensino básico na resolução de tarefasCatarina Fonseca | Escola Superior de Educação, Instituto Politécnico de Bragança Quarta-feira, 16 de julho, 9h00m - 10h00m Resumo Esta comunicação pretende apresentar e discutir aspetos de um estudo, ainda em desenvolvimento, que pretende identificar e analisar conexões estabelecidas por alunos dos 1.º e 2.º ciclos do ensino básico na resolução de tarefas. Integrando-se na prática de ensino supervisionada (PES) realizada no âmbito de um mestrado profissionalizante para a docência, é assumida a importância do estabelecimento de conexões de natureza diversa na aprendizagem dos alunos, podendo permitir-lhes abordagens e visões mais integradas do conhecimento. O estudo segue uma abordagem qualitativa, tendo os dados sido recolhidos através da observação participante e das produções dos alunos em ambiente de sala de aula e analisados com recurso à análise de conteúdo. Os resultados apontam para o estabelecimento, por parte dos alunos, de diversos tipos de conexões, mas também para algumas dificuldades em registar por escrito o seu reconhecimento. Notas biográficas Catarina Fonseca - Mestranda em Ensino do 1.º CEB e de Matemática e Ciências Naturais no 2.º CEB na Escola Superior de Educação do Instituto Politécnico de Bragança. A identificação e a análise de conexões, estabelecidas pelos seus alunos da prática de ensino supervisionada, constituem o principal objeto de estudo do seu relatório final de estágio, ainda em desenvolvimento. |
[Início_SC]
SC 07 | C Um manual escolar que conta uma história. O ensino da geometria.Alexandra Sofia Rodrigues | EDUNOVA.ISPA Centro de Investigação Interdisciplinar em Educação; CICS.NOVA Centro Interdisciplinar de Ciências Sociais; Faculdade de Ciências e Tecnologia da Universidade NOVA de Lisboa, UIED Quarta-feira, 16 de julho, 9h00m - 10h00m Resumo Entre 1947 e 1967, durante a formação técnica em Portugal, os alunos frequentaram o Ciclo Preparatório do Ensino Técnico. António Oleiro dos Santos Heitor, metodólogo, professor na Escola Industrial Marquês de Pombal e membro da Comissão para a reforma da Matemática Moderna no Ensino Técnico é o autor de um manual escolar de matemática para o 2.º ano ciclo preparatório, publicado em 1954. Nota biográfica Alexandra Sofia Rodrigues - Doutora em Didática da Matemática pela Universidade da Beira Interior. Tem um Mestrado em Educação Matemática, uma Especialização em Inovação e criatividade – as TIC e outra em Administração e Gestão Escolar. É professora auxiliar convidada na Faculdade de Ciências e Tecnologia da Universidade NOVA de Lisboa. Os interesses de investigação são diversificados, privilegiando a história da educação, o desenvolvimento curricular e o ensino e a aprendizagem da matemática no ensino profissional. |
[Início_SC]
SC 08 | A Formação de Professores em Ensino de Matemática com recurso à Tecnologia – Do Currículo Prescrito ao Currículo em AçãoPedro Pimenta | Escola Básica e Secundária do Monte de Caparica Quarta-feira, 16 de julho, 9h00m - 10h00m Resumo A literatura recomenda a integração da tecnologia digital nos currículos de Matemática para que se proporcionem aprendizagens significativas (Cai & Howson, 2013; NCTM, 2017), o que se faz nas novas Aprendizagens Essenciais (currículo prescrito) (DGE, 2021, 2023). Para que a tecnologia integre as práticas pedagógicas, é necessário implementar programas de desenvolvimento profissional (PDP), sustentáveis, para os professores em serviço. No entanto, a literatura aponta que a formação contínua de professores não tem tido o impacto esperado nas práticas pedagógicas. Nesta comunicação, referimo-nos à sustentabilidade (Zehetmeier & Krainer, 2011) dos PDP, refletindo sobre o conhecimento dos professores para ensinar matemática com tecnologia, como o GeoGebra, por referência a modelos teóricos como o modelo ALACT (Korthagen et al., 2001), TPACK (Koehler et al. (2013) e Génese instrumental e orquestração instrumentais (Rabardel, 1995; Trouche, 2004; Haspekian, 2013), preocupando-nos com a transformação do currículo prescrito no currículo em ação (Gimeno, 2000), tendo por base o trabalho de investigação em curso no âmbito do Doutoramento e Educação (Pimenta et. al, 2022a, 2022b, 2023, 2024; Pimenta & Silva, 2024). Terminamos com uma proposta de instrumento de avaliação para PDP, no âmbito do ensino de Matemática com recurso à tecnologia, partindo dos trabalhos de Bowers e Stephens (2011) e Akyuz (2018). Nota biográfica Pedro Pimenta - Licenciado em Matemática, ramo educacional, pela FCT/UNL. Mestre em Matemática para o Ensino pela FCUL. Doutorando em Educação (Inovação Educativa) na NOVA/ISPA. Formador acreditado de professores. Membro das comissões organizadoras do ProfNova e da ExpoFCT. Coautor dos projetos escolares Matemática a Giz de Cor, Sigma, Xis, Ípsilon, Novo Ípsilon, MatPower e Matemática 360. |
[Início_SC]
SC 08 | B Exposição Geometria Inquieta: uma experiência em um espaço não-formal durante um curso de formação continuada para professoresMarcelo de Oliveira Dias | Universidade Federal Rural do Rio de Janeiro (UFRRJ) Quarta-feira, 16 de julho, 9h00m - 10h00m Resumo A presente comunicação traz um relato de experiência com professores dos Anos Finais do Ensino Fundamental participantes de um curso de formação continuada sobre Habilidades de Geometria, durante a visitação da Exposição na Casa do Geometria Inquieta do artista Ascânio MMM. A exposição enfatiza dentre outros, a dialética entre projeto e execução, arte em espaços públicos, tridimensionalidade e composição planar. As esculturas expostas no jardim da Casa Roberto Marinho, estimulam desde o início da nossa visita ao olhar sobre a tridimensionalidade em conexão com a natureza. Nos salões, foi apresentada uma extensa mostra de todas as facetas de sua trajetória. As peças de Ascânio apresentam testes de limite, objetos não identificados e composições de figuras planas e figuras tridimensionais. Os docentes consideraram as dimensões informacional, social e interacional da experiência como muito positivas e foram inspirados a estruturarem atividades práticas em Geometria a partir das obras. Nota biográfica Marcelo de Oliveira Dias - Possui Licenciatura em Matemática pela Universidade Federal Rural do Rio de Janeiro e Doutorado em Educação Matemática pela Pontifícia Universidade Católica de São Paulo. É Pós doutor em Educação, especialidade em Didática da Matemática pelo Instituto de Educação da Universidade de Lisboa. Atualmente é Professor Associado do Departamento de Educação e Sociedade da Universidade Federal Rural do Rio de Janeiro e líder do Grupo de Pesquisa Currículo e Tecnologias Digitais em Educação Matemática. |
[Início_SC]
SC 09 | A Trabalho de Projeto “Notitia Mathesis: noticiário criativo de aprendizagem matemática”Eduardo Cunha | Agrupamento de Escolas de Barcelos Quarta-feira, 16 de julho, 9h00m - 10h00m Resumo Uma disciplina que desafia a lógica, a análise e a precisão pode também dar palco à criatividade, à comunicação e à colaboração. Nesta linha, foi lançada aos alunos de duas turmas do 10.º ano de Matemática A o desafio de transformar conteúdos matemáticos num noticiário pedagógico, rigoroso e criativo. Através da metodologia de Trabalho de Projeto os alunos deram forma a uma experiência de aprendizagem ativa, envolvente e com resultados surpreendentes, o projeto "Notitia Mathesis: noticiário criativo de aprendizagem matemática". Este projeto foi desenvolvido no âmbito da implementação das Aprendizagens Essenciais de Matemática A, mas também no contexto dos Laboratórios de Educação Digital (LED), enquadramento que possibilitou o uso de tecnologia de forma estruturada, sistemática e com propósito pedagógico claro. Nota biográfica Eduardo Cunha - Professor de Matemática A do quadro do Agrupamento de Escolas de Barcelos; membro do grupo trabalho T3 da APM; Mestre em Educação, especialização em Tecnologia Educativa, pela Universidade do Minho; Doutorando em Didáticas das Ciências e Tecnologia pela UTAD. |
[Início_SC]
SC 09 | B Problema de Fermi no âmbito das comemorações do 25 de abril de 1974 por alunos do 5.º ano de escolaridadeManuela Subtil | Agrupamento de Escolas Fragata do Tejo, Escola Superior de Educação de Lisboa, CICS.NOVA Quarta-feira, 16 de julho, 9h00m - 10h00m Resumo Esta comunicação visa analisar a resolução de um problema de Fermi no âmbito das comemorações do 25 de abril de 1974, por alunos do 5.o ano de escolaridade. Hipoteticamente, a comunidade educativa iria organizar uma festa. Era necessário acomodar os forasteiros que viriam de vários locais de Portugal. Os alunos teriam de fazer uma estimativa do número de pessoas que poderiam colocar a dormir na sala onde habitualmente tinham aulas de Matemática. Pretendeu-se que os alunos desenvolvessem conteúdos de acordo com as Novas Aprendizagens Essenciais da Matemática e competências no âmbito do Perfil dos Alunos à Saída da Escolaridade Obrigatória, tais como, Raciocínio e resolução de problemas, Pensamento crítico e pensamento criativo, Informação e comunicação e Relacionamento interpessoal. Metodologicamente, recorreu-se a uma investigação qualitativa de natureza interpretativa e descritiva, tendo se adotado a modalidade estudo de caso, os grupos. Os métodos utilizados para recolher os dados focaram-se nos registos escritos dos alunos e diário de bordo. Os alunos realizaram estimativas de quantas pessoas seria possível colocar a dormir na sala de aula de Matemática, não tendo evidenciado espírito critico. Nota biográfica Manuela Subtil - Professora de Matemática do grupo 500 e professora adjunta convidada do domínio científico de Matemática. É Licenciada e Mestre em Ensino de Matemática no 3.o Ciclo e Ensino Secundário e Doutora em Ciências da Educação. É autora de livros escolares e artigos publicados em revistas. Também tem publicados, posters e comunicações, em atas de congressos nacionais e internacionais. Tem participado em alguns projetos, sendo investigadora colaboradora do CICS.NOVA e UIED. |
[Início_SC]
SC 09 | C Portefólios Digitais na Disciplina de MatemáticaFilipa Susana da Graça Ferreira | AE Maria do Carmo Serrote, Sesimbra Quarta-feira, 16 de julho, 9h00m - 10h00m Resumo Nesta comunicação, pretende-se partilhar uma reflexão sobre a utilização dos portefólios digitais como instrumento para a aprendizagem à disciplina de Matemática, no contexto de turmas do 8.º e 9.º anos da Escola Básica do Agrupamento de Escolas Maria do Carmo Serrote, na Quinta do Conde, concelho de Sesimbra. A introdução deste recurso teve como principal finalidade melhorar as práticas pedagógicas e diversificar as estratégias de avaliação, promovendo uma abordagem mais formativa, centrada no aluno. O portefólio digital revelou-se um meio eficaz para acompanhar a evolução da aprendizagem, tornando visível o percurso de cada aluno: o que aprendeu, que dificuldades enfrentou e de que forma as superou. Serão ainda partilhadas as perceções dos alunos. Notas biográficas Filipa Susana da Graça Ferreira - Licenciada em Matemática (ramo educacional) e com uma especialização em Supervisão Pedagógica, é atualmente professora no Agrupamento de Escolas Maria do Carmo Serrote, na Quinta do Conde, concelho de Sesimbra. Ao longo do seu percurso profissional, tem desenvolvido um interesse particular pelas áreas da Didática da Matemática, dos processos de ensino, aprendizagem e avaliação, bem como pela integração das tecnologias digitais em contexto educativo. A sua prática letiva tem sido orientada por uma perspetiva reflexiva, procurando promover metodologias que valorizem o papel ativo do aluno na construção do conhecimento matemático. |
ProfMat 2025 - Sessões Especiais (60 min)
| SE 01 |
Educação e Matemática: Nós, professores de matemática (Resumo) Manuel Vara Pires, Helena Gil Guerreiro, Lina Brunheira, Paula Gomes e João Carlos Terroso, Equipa Editorial da EM 174 |
Anfiteatro 131 |
| SE 02 |
Agenda APM 2025/2026 "Dia-a-dia com a Matemática" (Resumo) Nélia Amado |
Auditório |
| SE 03 |
"40 anos de ProfMat: um resultado do trabalho colaborativo do GTHMEM" (Resumo) Alexandra Sofia Rodrigues e Mária Almeida |
Auditório |
SE 01 – Educação e Matemática: Nós, professores de matemáticaManuel Vara Pires, Helena Gil Guerreiro, Lina Brunheira, Paula Gomes e João Carlos Terroso, Equipa Editorial da EM 174 Terça-feira, 15 de julho, 17h30m - 18h30m Resumo Esta sessão especial é enquadrada pela revista temática de 2024 da Educação e Matemática focada no desenvolvimento profissional do professor, pretendendo constituir-se num merecido tributo a todos os professores de matemática. Para isso, é dada voz a professores de diferentes ciclos de ensino para partilharem connosco episódios significativos dos seus inspiradores percursos da vida de “ser professor de matemática”. Participação Manuela Vicente | Agrupamento de Escolas Gabriel Pereira, Évora |
SE 02 – Agenda 2025/2026 "Dia-a-dia com a Matemática"Nélia Amado Terça-feira, 15 de julho, 17h30m - 18h30m Resumo A edição 2025/2026 da Agenda "Dia-a-dia com a Matemática" foi elaborada pela APM, em parceria com a Câmara Municipal de Loulé. Propomos, nesta agenda, uma incursão pelo concelho de Loulé, através de vários problemas contextualizados que convidam à descoberta da cultura, do património e da riqueza arquitetónica desta região. Cada problema foi pensado a partir de situações reais, reforçando assim o elo entre a Matemática e o meio que nos rodeia. |
SE 03 – “40 anos de ProfMat: um resultado do trabalho colaborativo do GTHMEM”Alexandra Sofia Rodrigues e Mária Almeida Terça-feira, 15 de julho, 17h30m - 18h30m Resumo O GTHMEM – Grupo de Trabalho em História e Memórias do Ensino da Matemática, criado no seio da APM, realizou a sua primeira reunião a 1 de março de 1993, motivado pelo interesse crescente dos sócios e dos professores de Matemática pela integração da História da Matemática no ensino da disciplina. |
Exposições
PROFMAT/85 – O PRIMEIRO / Na origem, um encontro – hoje, uma história com muitos capítulos
GTHMEM – Grupo de Trabalho de História e Memórias do Ensino da Matemática

O Encontro de Professores ProfMat teve a sua primeira edição em 1985, em Lisboa. Quarenta anos depois, celebramos um percurso rico em partilhas, reflexões e aprendizagens.
Para assinalar esta data especial, o GTHMEM – Grupo de Trabalho de História e Memórias do Ensino da Matemática – organizou uma exposição dedicada ao primeiro ProfMat. A mostra recorda os acontecimentos que estiveram na origem do encontro e apresenta, em detalhe, o seu programa: sessões plenárias, grupos de discussão, mesas redondas e trabalhos de investigação que marcaram o início desta importante tradição.
Parabéns, ProfMat
40 ANOS DE PROFMAT / Uma viagem pela memória de um encontro que marcou gerações
GTHMEM – Grupo de Trabalho de História e Memórias do Ensino da Matemática

O Encontro de Professores de Matemática ProfMat celebra 40 anos! Quatro décadas consecutivas de promoção da reflexão, da partilha e do trabalho colaborativo em torno do ensino e da aprendizagem da Matemática.
Esta exposição, concebida no seio do GTHMEM – Grupo de Trabalho de História e Memórias do Ensino da Matemática, assinala esta data tão especial com um olhar afetivo e histórico sobre o percurso do ProfMat. A proposta ganhou forma num registo livre e criativo, que convida à viagem no tempo e à celebração da memória coletiva do encontro.
A mostra reúne 40 cartazes – um por cada edição do ProfMat – acompanhados de testemunhos em vídeo de participantes do primeiro encontro. Sabemos que um cartaz não basta para expressar toda a riqueza de cada edição, mas procurámos destacar os elementos mais emblemáticos e representativos de cada ano.
Porque recordar é reviver, esperamos que esta exposição desperte memórias felizes, enquanto reforça o entusiasmo para continuarmos a construir com os que vão chegando muitos mais capítulos desta história partilhada.
RECORDAR HENRIQUE GUIMARÃES
(1951 - 2022)
E unicamente ao movimento de crescer nos guiasse. Termos das árvores
A incomparável paciência de procurar o alto
A verde bondade de permanecer
E orientar os pássaros
(Daniel Faria, in Explicação das árvores e de outros animais, 1998)
Esta é uma presença outra do Henrique entre nós, habituados que estávamos a vê-lo, a conversar com ele, a assistir às suas conferências nos ProfMats que ele seguiu na totalidade, inscrevendo-se e participando sempre.
RECORDAR EDUARDO VELOSO
(1928 - 2022)
Recordar o Eduardo Veloso é uma exposição que revisita algumas ideias significativas daquele que foi um dos sócios fundadores da APM, grande entusiasta e animador de muitas das atividades associativas.
Esta exposição, cuja ideia partiu de uma proposta da direção da APM, foi pensada pelos seus organizadores como uma oportunidade de expor algumas das principais ideias do Eduardo Veloso sobre a APM, a Educação em geral e o Ensino da Matemática, ideias que defendia consistentemente, sempre numa base de grande coerência, e que partilhava muitas vezes informalmente numa primeira fase para depois passar a escrito e divulgar ou defender em fóruns diversos.
ProfMat 2025 - Sessões Complementares
|
Geometria do corpo e da mente As sessões da Geometria do Corpo e da Mente são uma novidade do ProfMat e SIEM 2025. Nelas os participantes estarão imersos numa experiência de yoga. Tranquilizando a mente, o movimento do corpo flui ao ritmo da respiração, a linguagem matemática e os conceitos geométricos ganharão harmonia com as posturas corporais e em conexão com o interior de cada um. Nenhum outro acessório além da presença de cada um será requerido para usufruir desta experiência. Estas sessões serão orientadas por Maria Glória Garcia. |
|
Trilho matemático Um trilho matemático pode ser definido como percurso com pontos de interesse ou estações para despertar possíveis relações entre a matemática e o meio envolvente, em qualquer lugar. No trilho pensado para o ProfMat 2025 vamos percorrer algumas ruas da emblemática cidade de Évora, com paragens em locais onde serão colocados desafios no sentido de proporcionar experiências que integrem o conhecimento matemático, histórico e artístico com aspetos da cultura local. A distância do percurso está compreendida entre 2 e 3 quilómetros. |
|
Salas de azulejos Sabia que todas as salas do claustro do Colégio Espírito Santo têm a particularidade de estarem revestidas por azulejos de acordo com os temas que, em tempos, aí foram ensinados? Desde a Filosofia Grega à Geografia, da Geometria à Sagrada Escritura ou Cenas de Caça e Pesca, venha conhecer as histórias que nos contam estes azulejos nas visitas guiadas. |
XXXV SIEM — Apresentação
O SIEM – Seminário de Investigação em Educação Matemática vai ter a sua XXXV edição nos dias 16 e 17 de julho de 2025 em Évora. Realizado em coordenação com o ProfMat, com algumas sessões conjuntas, constitui um momento de apresentação de trabalhos e discussão privilegiado para todos os que se interessam pela investigação em Educação Matemática. Com um programa intenso que inclui três conferências plenárias, um painel plenário, duas sessões de simpósios de comunicações, um espaço GTI, um momento especial sobre Geometria e um jantar-convívio, o Seminário irá permitir múltiplos debates sobre as aprendizagens dos alunos, a formação dos professores, os currículos e os materiais de ensino proporcionando um aprofundamento de perspetivas e conhecimento e o estreitamento de laços de colaboração entre os participantes.
Bem-vindo ao SIEM!
Comissões — SIEM
COMISSÃO ORGANIZADORA - XXXV SIEM
Ana Margarida Neves
Ana Paula Canavarro
António Borralho
Beatriz Martins
Hélia Pinto
Joana Latas
João Pedro da Ponte
Joaquim Pinto
Lurdes Serrazina
Nadia Ferreira
Teresa Gonçalves
COMISSÃO CIENTÍFICA - XXXV SIEM
Ana Barbosa, inED, Instituto Politécnico de Viana do Castelo, Portugal
Ana Caseiro, Escola Superior de Educação de Lisboa, Instituto Politécnico de Lisboa, Portugal
Ana Elisa Esteves Santiago , Escola Superior de Educação de Coimbra, Instituto Politécnico de Coimbra, Portugal
Ana Isabel Silvestre, ESECS, Ci&DEI, Instituto Politécnico de Leiria, Portugal
Ana Oliveira, ESECS, Ci&DEI, Instituto Politécnico de Leiria, Portugal
Ana Paula Canavarro, Universidade de Évora, Portugal
Angelica Francisca de Araujo, Universidade Federal Rural do Rio de Janeiro, Brasil
António Domingos, EDUNOVA.ISPA e CICS.NOVA, NOVA FCT, Portugal
António Guerreiro, Universidade do Algarve, Portugal
António Borralho, Universidade de Évora, Portugal
Berta Barquero Farràs, Departament d’Educació Lingüística, Científica i Matemàtica, Facultat d’Educació. Campus Mundet - Universitat de Barcelona, Espanha
Carlos Miguel Ribeiro, Universidade Estadual de Campinas (UNICAMP), Brasil
Catarina Delgado, Escola Superior de Educação, Instituto Politécnico de Setúbal, Portugal
Célia Mestre, Escola Superior de Educação, Instituto Politécnico de Setúbal, Portugal
Cláudia Torres, AE D. Dinis Lisboa, Projeto #EstudoEmCasa Apoia, Ministério da Educação, Ciência e Inovação, Portugal
Cristina Martins, Centro de Investigação Transdisciplinar em Educação e Desenvolvimento, Departamento de Matemática, Escola Superior de Educação, Instituto Politécnico de Bragança, Portugal
Dina Tavares, ESECS, Ci&DEI, Instituto Politécnico de Leiria, Portugal
Elsa Isabelinho Barbosa, Centro de Investigação em Educação e Psicologia, Universidade de Évora, Portugal
Ema Mamede, Universidade do Minho, Portugal
Fátima Regina Jorge, Instituto Politécnico de Castelo Branco, Portugal
Fernando Martins, Instituto Politécnico de Coimbra, ESEC, Portugal
Helena Martinho, CIEd-UM, Universidade do Minho, Portugal
Helena Rocha, EDUNOVA.ISPA, CICS.NOVA, FCT, Universidade NOVA de Lisboa, Portugal
Hélia Jacinto, Instituto de Educação, Universidade de Lisboa, Portugal
Hélia Oliveira, Instituto de Educação, Universidade de Lisboa, Portugal
Hélia Pinto, ESECS, CI&DEI, Instituto Politécnico de Leiria, Portugal
Hugo Menino, ESECS, CI&DEI, Instituto Politécnico de Leiria, Portugal
Isabel Lucena, Universidade Federal do Pará, Brasil
Isabel Vale, Instituto Politécnico de Viana do Castelo, Portugal
Joana Latas, Universidade de Évora, Centro de Investigação em Educação e Psicologia (CIEP), Portugal
João Pedro Ponte, Instituto de Educação da Universidade de Lisboa, Portugal
Joaquim Pinto, Departamento de Educação e Psicologia da Universidade de Aveiro, Portugal
Jorge Henrique Gualandi, Instituto Federal do Espírito Santo, Campus Cachoeiro de Itapemirim, Brasil
Lina Fonseca, CIEC-UM, Instituto Politécnico de Viana do Castelo, Portugal
Maria Alexandra Oliveira Gomes, CIEC-IE, Universidade do Minho, Portugal
Maria de Fátima Fernandes, inED, Instituto Politécnico de Viana do Castelo, Portugal
Maria de Lurdes Serrazina, Escola Superior de Educação de Lisboa, Instituto Politécnico de Lisboa, Portugal
Manuel Vara Pires, CITeD, Instituto Politécnico de Bragança, Portugal
Margarida Rodrigues, Escola Superior de Educação do Instituto Politécnico de Lisboa, Ci&DEI, Portugal
Maria Cristina Costa, Unidade Departamental de Matemática e Física do Instituto Politécnico de Tomar (IPT), Centro de Investigação em Cidades Inteligentes do IPT, Portugal
Maria de Fátima Mendes, CIEQV, Departamento de ciências e Tecnologias, Instituto Politécnico de Setúbal, Portugal
Maria Teresa Fernandez Blanco, Facultade de Ciencias da Educación (Campus Norte), Universidade de Santiago de Compostela, Espanha
Maria José Costa dos Santos, Universidade Federal do Ceará, Brasil
Marina Rodrigues, ESECS, CI&DEI, Instituto Politécnico de Leiria, Portugal
Marisa Quaresma, Instituto de Educação, Universidade de Lisboa, Portugal
Nadia Ferreira, EDUINOVA.ISPA / ISPA, Instituto Universitário, Portugal
Nélia Amado, Faculdade de Ciências e Tecnologia, Universidade do Algarve, Portugal
Neusa Branco, Instituto Politécnico de Santarém, Portugal
Nicole Duarte, ESECS, CI&DEI, Instituto Politécnico de Leiria, Portugal
Paula Teixeira, Agrupamento de Escolas João de Barros, Portugal
Paulo Martins Afonso, Escola Superior de Educação do Instituto Politécnico de Castelo Branco, Portugal
Pedro José Arrifano Tadeu, ESECD, CI&DEI, Instituto Politécnico da Guarda, Portugal
Raquel Santos, Instituto Politécnico de Santarém, Portugal
Rita Cadima, CIDMA, CI&DEI, Instituto Politécnico de Leiria, Portugal
Rosa Ferreira, Universidade do Porto, Portugal
Susana Colaço, ESE-IPSantarém, Pólo de Literacia Digital e Inclusão Social (CIAC), Portugal
Teresa Neto, Departamento de Educação e Psicologia da Universidade de Aveiro, Portugal
Locais do SIEM
O XXXV SIEM decorre na Universidade de Évora, a parte comum com o ProfMat2025 continuará a decorrer no Colégio Espírito Santo, a parte não comum será acolhida pelo Centro de Investigação em Educação e Psicologia da Universidade de Évora, no Colégio Pedro da Fonseca.
COLÉGIO ESPÍRITO SANTO
Clique sobre a imagem para pesquisar no mapa:
COLÉGIO PEDRO DA FONSECA
Localização:
latitude/longitude: 38.55014563805449 /-7.91440486907959
GPS eXchange (.gpx) | ViaMichelin (.xvm)
Morada:
Rua da Barba Rala, N.º 1,
7005-345
Évora
Email:
ciep@uevora.pt
Telefone:
+351 266 768 050
url:
Programa — SIEM
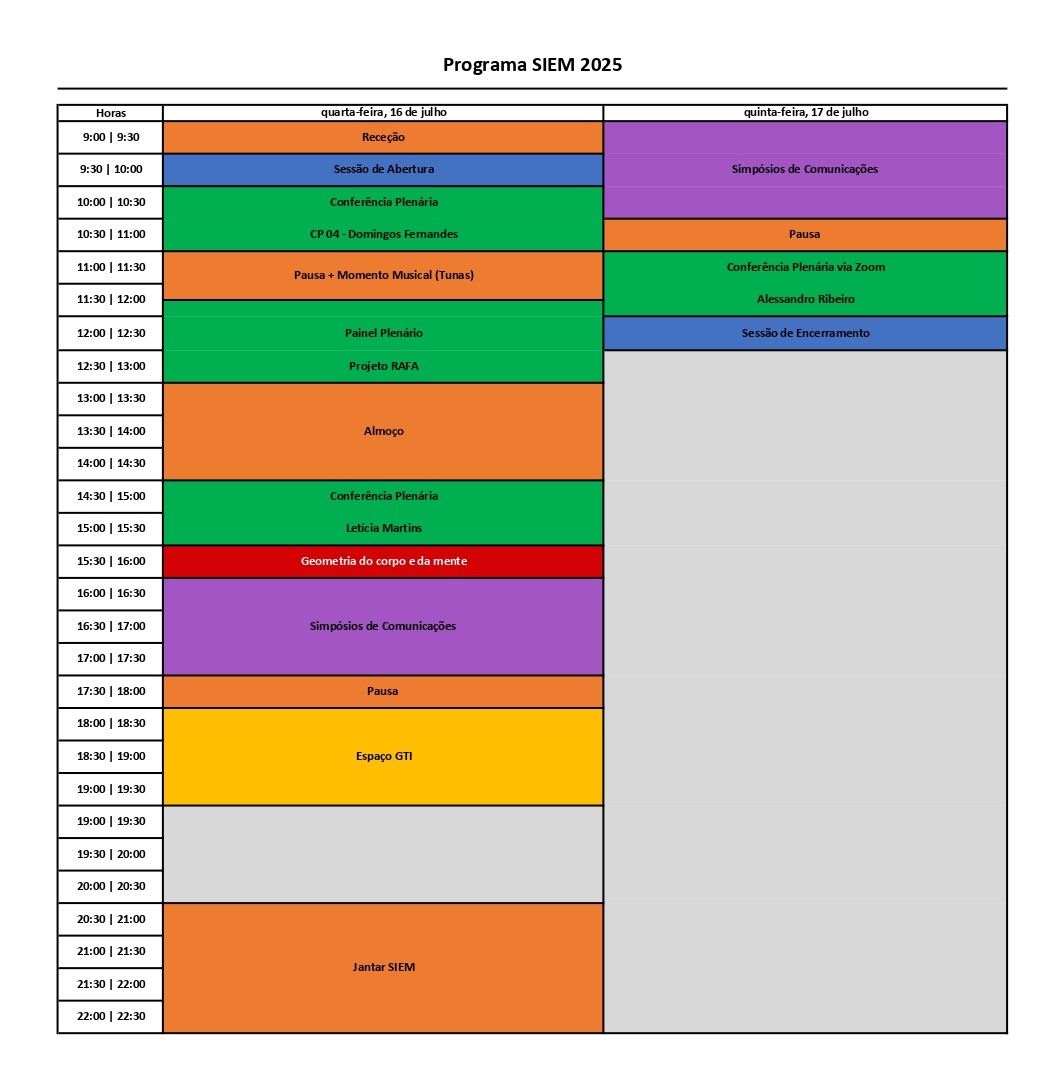
Geometria do corpo e da mente
As sessões da Geometria do Corpo e da Mente são uma novidade do ProfMat e SIEM 2025. Nelas os participantes estarão imersos numa experiência de yoga. Tranquilizando a mente, o movimento do corpo flui ao ritmo da respiração, a linguagem matemática e os conceitos geométricos ganharão harmonia com as posturas corporais e em conexão com o interior de cada um. Nenhum outro acessório além da presença de cada um será requerido para usufruir desta experiência. Estas sessões serão orientadas por Maria Glória Garcia.
Submissão de Comunicações e Pósteres
Os participantes no SIEM podem submeter propostas de comunicações e/ou pósteres, a serem apresentadas em simpósios com discussão. As comunicações têm 15 minutos para apresentação e os pósteres têm 5 minutos para apresentação. Todos os trabalhos serão sujeitos a revisão científica por pares, com base em critérios uniformes indicados pela comissão científica relativos a clareza, estrutura, relevância e coerência da proposta. As propostas devem seguir rigorosamente as indicações formais abaixo fornecidas e serem enviadas até 2 de junho, através dos formulários abaixo.
A notificação de aceitação é realizada pela comissão científica até 16 de junho e a submissão da versão final revista para publicação em atas tem de ser enviada até 30 de junho.
As atas do XXXV SIEM irão ser propostas para indexação na Web of Science.
COMUNICAÇÕES
O texto da comunicação será publicado nas Atas se respeitar rigorosamente as normas de formatação que constam no modelo.
Modelo para submissão de Comunicação
| Submissão de Comunicação |
PÓSTERES
O texto do póster será publicado nas Atas se respeitar rigorosamente as normas de formatação que constam no modelo.
Modelo para submissão de Póster
| Submissão de Póster |
Modelo de PowerPoint
Se vai apresentar alguma comunicação e/ou póster e pretende utilizar um modelo comum, próprio deste SIEM, descarregue-o aqui:
Almoço | Jantar do SIEM
Durante o SIEM, pode reservar as seguintes opções para almoçar:
| Preço | Pratos | 16 julho | 17 julho | |
|
Cozinha do Cardeal (máx. 60 lugares) |
18 euros |
Peixe Carne Vegetariano |
||
|
Colégio Luís de Verney (máx. 190 lugares) |
10 euros |
Peixe Carne Vegetariano |
||
|
Colégio Pedro da Fonseca (máx. 60 lugares) |
10 euros |
Peixe Carne Vegetariano |
Cada almoço na "Cozinha do Cardeal" tem um custo de 18 euros, e no "Colégio Luís de Verney" ou no "Colégio Pedro da Fonseca" estes dois um custo de 10 euros, pagos no ato de inscrição.
Jantar do SIEM 2025 - Quarta-feira 16 de julho, às 20:30
Mar De Ar Muralhas
URL: https://mardearhotels.com/
 |
 |
EMENTA
Sopa: Creme de espargos verdes
Peixe:Corvina corada com molho de natas ácidas, com tagliatelle de espinafres
Carne: Lombo de porco assado recheado com farinheira com batatas à padeiro
Seleção de frios & saladas, sobremesas e bebidas
XXXV SIEM — Atas
As atas do XXXV SIEM irão ser propostas para indexação na Web of Science.
Contactos
siem2025@apm.pt
XXXV SIEM - Associação de Professores de Matemática
Rua Dr. João Couto, n.º 27-A
1500-236 Lisboa
Tel.: +351 21 716 36 90 / 21 711 03 77
 |
 |
 |
 |
XXXV SIEM - Conferências Plenárias (1h)
Para melhorar as Políticas e Práticas Educativas: Contributos do Conselho Nacional de EducaçãoDomingos Fernandes, Conselho Nacional de Educação, Centro de Investigação e Estudos em Sociologia — Instituto Universitário de Lisboa (Iscte) Quarta-feira, 16 de julho, 10h00m - 11h00m Resumo O Conselho Nacional de Educação (CNE), órgão independente e de consulta da Assembleia da República e do Governo, através das suas publicações periódicas (Estado da Educação e DICA – Divulgar, Inovar, Colaborar, Aprender), assim como dos pareceres, recomendações e contributos diversos, materializa o acompanhamento e a avaliação que vai fazendo acerca das políticas e práticas educativas. Nesta conferência, apresentam-se e discutem-se algumas questões críticas que emergem das posições expressas pelo CNE no Estado da Educação 2023 e também das investigações e narrativas de projetos constantes no DICA 2024. Salientam-se, por um lado, questões relativas à estrutura do sistema educativo (e.g., Educação dos 0 aos 12 anos e Educação Secundária) e, por outro lado, questões relativas ao Currículo e à Inovação Pedagógica, à Formação de Professores, e à Equidade, Democratização e Qualidade da Educação. A partir das questões suscitadas, fazem-se considerações e produzem-se reflexões acerca de relações entre a investigação considerada necessária para fundamentar e melhorar as políticas e práticas educativas. Nota biográfica
Domingos Fernandes – Presidente do Conselho Nacional de Educação desde 9 de junho de 2022. Investigador no Centro de Investigação e Estudos de Sociologia (ISCTE). Os seus interesses de investigação decorrem das Relações entre Currículo, Pedagogia e Avaliação. Professor visitante em diversas universidades internacionais. Investigador principal de projetos financiados no âmbito de concursos públicos. O seu artigo mais recente intitula-se Conhecimento, discernimento e ação em avaliação pedagógica: O legado de Leonor Santos publicado em 2024 na revista Quadrante da APM.
|
CP 01 – Compreeder os contributos mútuos entre a resolução de problemas e a comunicação escritaLetícia Gabriela Martins, CIEd - Universidade do Minho
Quarta-feira, 16 de julho, 14h30m - 15h30m
Resumo A resolução de problemas e a comunicação escrita são duas das ideias chave apresentadas nas aprendizagens essenciais para a disciplina de Matemática. São dois dos fatores que contribuem para a compreensão matemática, além de que têm uma forte ligação entre eles – isto porque quando um aluno resolve um problema, importa que seja capaz de comunicar o seu raciocínio a um colega ou ao professor. Os alunos devem ser incentivados a resolver problemas e a justificar as suas resoluções, encadeando devidamente as suas ideias e raciocínios, com a utilização de múltiplas representações adequadas e com clareza. Assim, torna-se importante analisar o modo como os alunos comunicam, nomeadamente por escrito, para se perceber que fatores podem ser melhorados. Ao proporcionar aos alunos oportunidades de resolver problemas com o uso de diferentes estratégias, incentivando-os a escrever as suas resoluções e a debatê-las com os colegas, estamos a fazer com que desenvolvam diferentes competências importantes para o ensino e aprendizagem da Matemática. Nesta conferência, apresento categorias de análise que podem ajudar numa avaliação formativa da resolução de problemas, bem como análise de exemplos concretos.
Nota biográfica
|
CP 02 – Como podemos aprender a ensinar matemática a partir de nossas próprias salas de aulaAlessandro Jacques Ribeiro, Centro de Matemática, Computação e Cognição (CMCC), Universidade Federal do ABC (UFABC)
Quinta-feira, 17 de julho, 11h00m - 12h00m Resumo O professor é um dos elementos mais relevantes e essenciais para a aprendizagem dos alunos. No entanto, muitas vezes nos esquecemos como também é importante e essencial focarmos nossas atenções para a aprendizagem dos professores. Situando a discussão no âmbito da Matemática, na presente conferência pretende-se problematizar o que, como e com que finalidade o professor de matemática aprende a ensinar essa disciplina na escola básica. Trazendo situações de aulas de matemática, iremos discutir a aprendizagem profissional do professor a partir de sua própria prática letiva, quando o professor é convidado a vivenciar tarefas formativas contemplando, por exemplo, respostas de estudantes, planos de aula, vídeos de aulas implementadas no terceiro ciclo e no do ensino secundário. Os resultados apresentados pretendem propiciar reflexões nos assistentes sobre como aprender a partir da própria prática pode não só reorganizar crenças e conhecimentos dos professores, mas também, oferecer oportunidades para que sejam repensadas suas próprias práticas letivas. Implicações para a pesquisa e para a profissão docente serão exploradas. Nota biográfica
|
XXXV SIEM - Painel Plenário (1h15)
Sessão especialmente organizada para promover uma discussão sobre um tema de atualidade, com vários intervenientes convidados para o efeito. É preparada e conduzida por um moderador convidado pela organização que solicita intervenções dos vários participantes do painel sobre o tema em discussão e em resposta a questões da assistência que em momento próprio é convidada a intervir.
Projeto RAFA: Relações entre Avaliação Formativa e as Aprendizagens na aula de matemáticaModerador: Marcelo Coppi, Universidade de Évora Intervenientes: António Borralho, Universidade de Évora Quarta-feira, 17 de julho, 11h30m - 13h00m Resumo A investigação tem-nos mostrado que é frequente os processos de ensino e das aprendizagens dos alunos decorrerem de forma articulada na sala de aula, não havendo uma separação entre quando um acaba e o outro começa. Recorrentemente estes processos são analisados de forma conjunta e complementar. Mas, quando é para avaliar há um momento específico para tal, ou seja, é um processo algo independente dos processos de ensino e de aprendizagem – há uma quebra. Parou, que agora vamos avaliar! Porquê? Neste contexto, foi desenvolvido um modelo didático inovador que emergiu de um estudo empírico com foco na análise e articulação entre os processos de ensino, avaliação e aprendizagem numa sala de aula de matemática do 7.º ano de escolaridade, no âmbito de um projeto de investigação mais alargado. Os resultados da implementação do modelo evidenciam que as práticas letivas em estreito relacionamento com a implementação de tarefas incluindo propósitos de ensino, avaliação e aprendizagem, bem como com o currículo, são consistentes com o desenvolvimento da autorregulação das aprendizagens e da participação dos alunos, o que conduziu a uma melhoria nas suas aprendizagens.
Marcelo Coppi - Assistente Convidado na Universidade de Évora (Departamento de Pedagogia e Educação) e doutorando em Ciências da Educação. Como investigador no Centro de Investigação em Educação e Psicologia da Universidade de Évora, desenvolve projetos e publica nas áreas da avaliação pedagógica, literacia científica e formação de professores.
António Borralho - Doutor em Ciências da Educação (Educação Matemática) pela Universidade de Évora, mestre em Tecnologia Educativa pela Universidade de Salamanca (Espanha) e licenciado em Ensino de Matemática e Desenho pela Universidade de Évora. É Professor Associado da Universidade de Évora e membro integrado do Centro de Investigação em Educação e Psicologia. A educação matemática é o seu principal interesse de investigação, tendo as suas publicações incidido na didática e na avaliação das aprendizagens.
Elsa Barbosa - Doutora em Ciências da Educação (Educação Matemática), mestre em Educação Matemática e licenciada em Matemática (Ensino de) pela Universidade de Évora. Membro integrado no Centro de Investigação em Educação e Psicologia da mesma universidade. Professora de Matemática exercendo, atualmente, o cargo de subdiretora do AE Manuel Ferreira Patrício. Participa em redes de investigação associadas a universidades federais no Brasil. A educação matemática é o seu principal interesse de investigação.
Joana Latas - Doutora em História das Ciências e Educação Científica pela Universidade de Coimbra, mestre em Ciências da Educação – Supervisão Pedagógica e licenciada em Matemática e Ciências da Computação pela Universidade de Évora. É membro integrado do Centro de Investigação em Educação e Psicologia da Universidade de Évora e professora de Matemática. Tem investigação publicada na área da educação matemática, educação científica em contextos não formais e em avaliação pedagógica
Maria João Rocha - Terminou a licenciatura em Ensino Básico 1º ciclo, pela Universidade de Évora, no ano de 2002 e, desde então, desempenhou funções como docente titular de turma e como docente de apoio educativo, em diferentes agrupamentos do Alentejo e da região de Lisboa. Desde 2021, exerce funções como docente titular de turma, atualmente numa turma de 2º ano, na Escola Básica da Cruz da Picada, pertencente ao Agrupamento de Escolas Manuel Ferreira Patrício, em Évora. É também professora Cooperante no âmbito da parceria com a Universidade de Évora.
|
XXXV SIEM - Simpósios de Comunicações e Pósteres



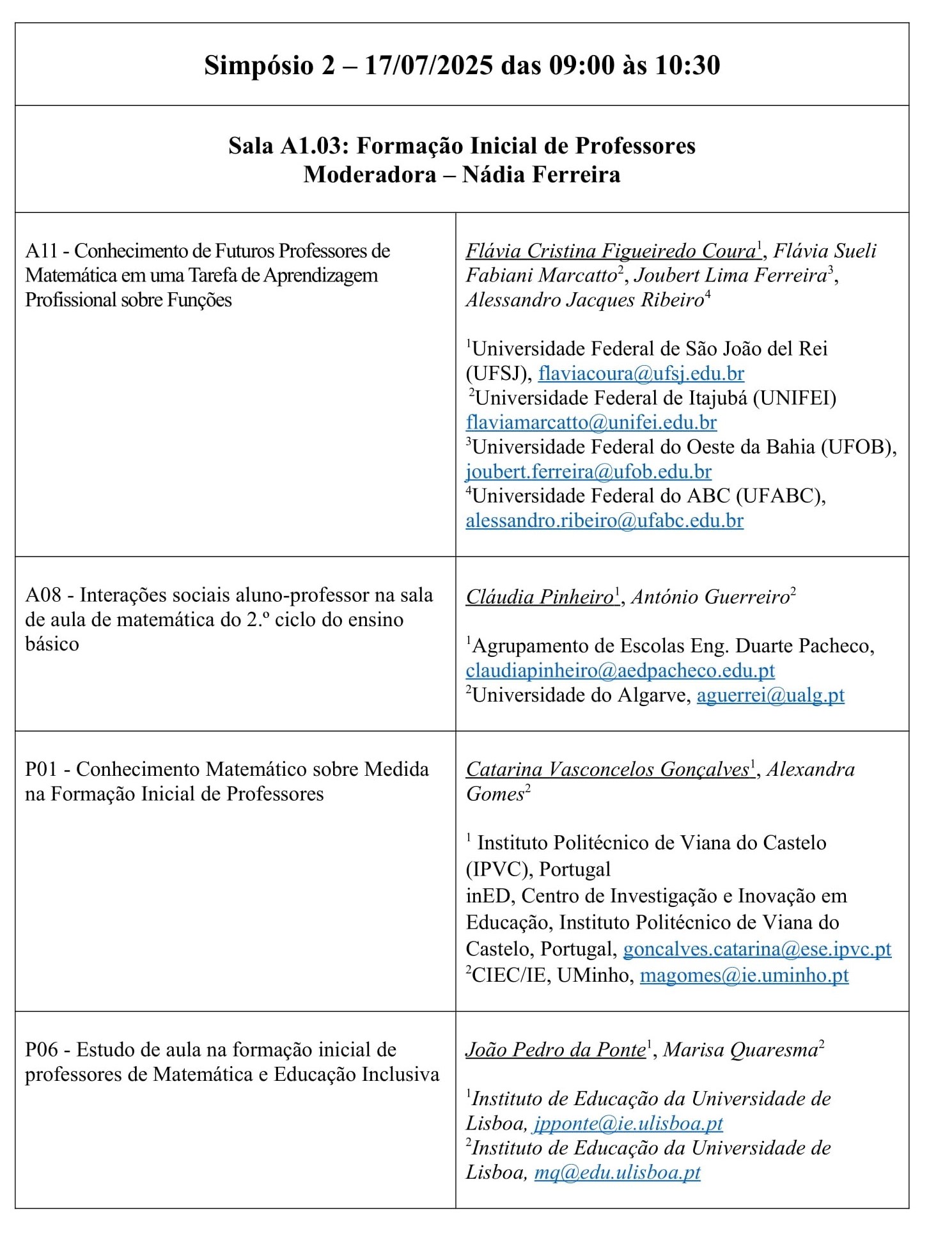
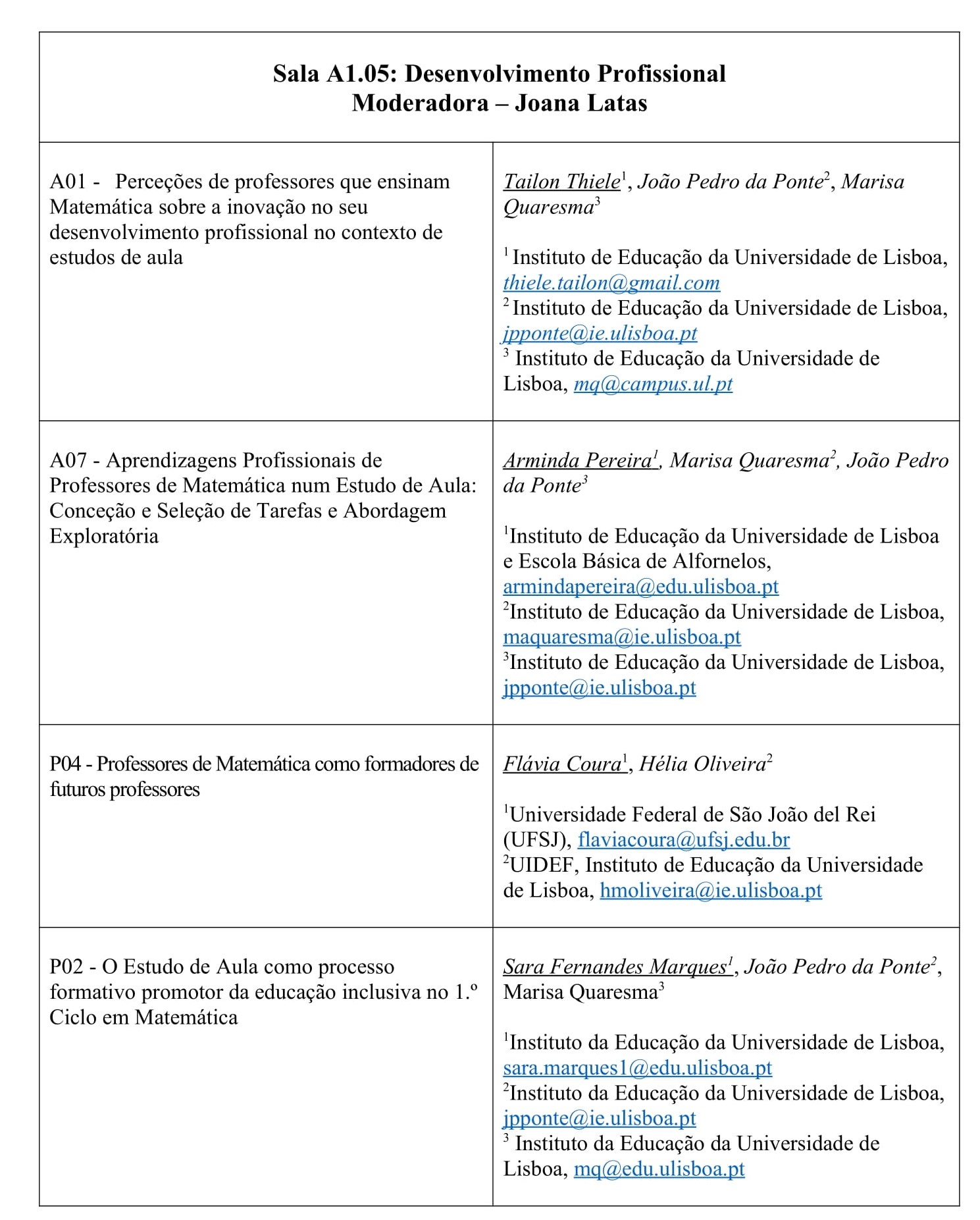
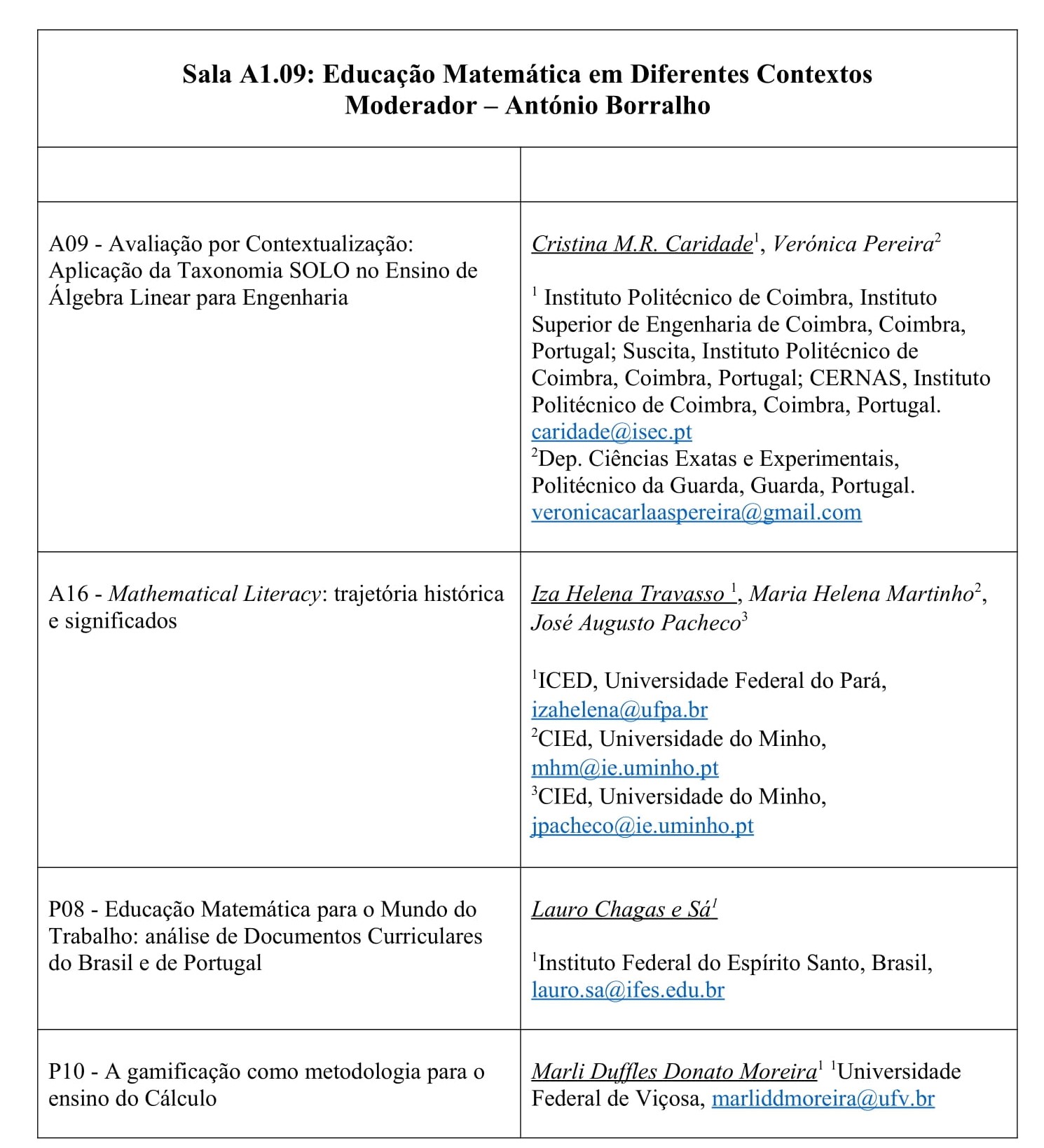
RESUMOS | ABSTRACTS
.jpg)
(1).jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
XXXIV SIEM - ESPAÇO GTI
Investigação e Aprendizagens Essenciais do Ensino SecundárioModerador: Cláudia Maria Canha Nunes Johnen Torres, Coordenadora Projeto #EstudoEmCasa Apoia e docente do AE D. Dinis Participantes: António Domingos, Faculdade de Ciências da Universidade Nova de Lisboa Quarta-feira, 17 de julho, 17h00m - 18h00m Resumo O espaço GTI constituiu-se como um espaço informal de troca de ideias sobre um tema da atualidade para a investigação em Educação Matemática. Este ano propomos dar sequência à reflexão iniciada no ano anterior e conversar com membros das equipas das Aprendizagens Essenciais (AE) do Ensino Básico e do Ensino Secundário sobre o papel desempenhado pela investigação no desenvolvimento e implementação das mesmas. Em concreto debateremos como a investigação suporta a organização da formação de professores e o desenvolvimento de materiais curriculares de apoio às AE, para além da definição das próprias AE. Notas biográficas
António Domingos – Licenciado em Matemática e Desenho, Mestre em Ciências da Educação e Doutor e na mesma área, com a especialidade de Teoria e Desenvolvimento Curricular, ambas as especializações realizadas na Faculdade de Ciências e Tecnologia da UNL. Professor Auxiliar no Departamento de Ciências Sociais Aplicadas da FCT NOVA, lecionando no Mestrado em Ensino da Matemática, no Mestrado em Educação e o Programa Doutoral em Educação NOVA-ISPA. É investigador do CICS NOVA e coordenador da UIED, onde tem participado em vários projetos de investigação financiados. É sócio de várias associações profissionais tendo integrado a Direção da APM e sendo atualmente membro da Direção da SPIEM. Os principais interesses de investigação prendem-se com as questões relacionadas com o Ensino e Aprendizagem da Matemática, a integração das Tecnologias no Ensino e Aprendizagem, o Desenvolvimento Curricular em Matemática e aspetos relacionados com a História do Ensino da Matemática.
Susana Carreira – Professora Associada da Faculdade de Ciências e Tecnologia da Universidade do Algarve e Professora Associada Convidada do Instituto de Educação da Universidade de Lisboa. É doutorada em Didática da Matemática pela Universidade de Lisboa. Desenvolve investigação em Educação Matemática, nomeadamente nas seguintes áreas: modelação e aplicações no ensino e aprendizagem da matemática; tecnologias na educação matemática, resolução de problemas, criatividade matemática, aspetos afetivos na educação matemática. É autora de livros e artigos científicos em revistas nacionais e internacionais. Tem orientado estudantes de mestrado e de doutoramento, em Portugal e no Brasil. Fez parte da equipa que elaborou as novas Aprendizagens Essenciais de Matemática para o ensino secundário, homologadas em 2023. |
Espetáculo: A Peste
ESPETÁCULO: A PESTE
Segunda-feira, 15 de julho, 21h30m - 22h30m
Local: Auditório da Escola Secundária Rafael Bordalo Pinheiro
LOTAÇÃO: 200 PESSOAS
Grupo de Teatro "Os Bordalitos"
Título do Espetáculo: A Peste
Dramaturgia: Criação coletiva baseada em “Estado de Sítio” de Albert Camus
Direção: Amábile Maria
Elenco:
Ana Silva
Carmem Stroo Cloeck
Charlie
Constança Fonseca
Cléo
Diogo Jesus
Fernanda Monteiro
Letícia Pinheiro
Maria Lima
Mathis Audigane
Matilde Lima
Sal S. Nicolau
Sinopse:
"Estado de Sítio", de Albert Camus, é uma peça teatral que examina a natureza do poder, da liberdade e da resistência face à opressão. Retrata um regime totalitário que controla seus cidadãos através do medo e da subjugação. Quando a cidade de Caldas da Rainha é colocada como cenário, a história ganha uma dimensão atual e passa a questionar: quais são os absurdos do mundo de hoje? O que aconteceria se o absurdo se transformasse em lei? Enquanto os habitantes lutam para preservar sua liberdade, a peça explora as tensões do autoritarismo e da democracia."
Visitas guiadas
VISITAS GUIADAS ÀS CALDAS DA RAINHA
Visitas organizadas pelo Município das Caldas da Rainha - Unidade de Turismo
Terça-feira, 16 de julho, 18h30m - 19h30m
Para cada uma das tês visitas, foram selecionados 35 participantes, de acordo com a ordem de inscrição no ProfMat/SIEM e atendendo às preferências indicadas no formulário de inscrição. As listas de participantes selecionados serão afixadas no Centro Cultural e de Congressos.
Local de partida: Centro Cultural e de Congressos (Praça da Animação)
Visita 1 - História e património termal das Caldas da Rainha
Visita 1 - Visita ao complexo termal, a zona fundacional da cidade. Os visitantes terão oportunidade de compreender a história da cidade, com uma visita ao Hospital Termal.
Visita 2 - Percurso das águas termais das Caldas da Rainha
Visita 2 - Contextualização histórica e científica do percurso das águas termais. Esta visita terá lugar na Mata Rainha Dona Leonor, erguida para proteger as nascentes das águas termais.
Visita 3 - Parque D. Carlos I, História e biodiversidade
Visita 3 - Visita ao Parque D. Carlos I, parque romântico do século XIX, localizado no coração da cidade. Através desta visita, irá saber um pouco mais da sua história e origens, assim como a biodiversidade que o compõe e enriquece.
Prazos
PROFMAT 2025
| Inscrição ProfMat 1.º prazo (ADIAMENTO) | até 14 de junho |
| Submissões de Sessão Práticas e/ou Comunicações | até 31 de maio |
| Notificação de aceitação | até 15 de junho |
| Inscrição ProfMat 2.º prazo | até 29 de junho |
| Inscrição ProfMat 3.º prazo | após 29 de junho |
SIEM 2025
| Inscrição SIEM 1.º prazo (ADIAMENTO) | até 14 de junho |
| Submissões de Comunicações e/ou Pósteres | até 2 de junho |
| Notificação de aceitação e indicações de revisão | até 16 de junho |
| Submissão da versão final revista para publicação em atas | até 30 de junho |
| Inscrição sem multa para autores Comunicações/Pósteres | até 29 de junho |
| Inscrição SIEM 2.º prazo | até 29 de junho |
| Inscrição SIEM 3.º prazo | após 29 de junho |
Preços
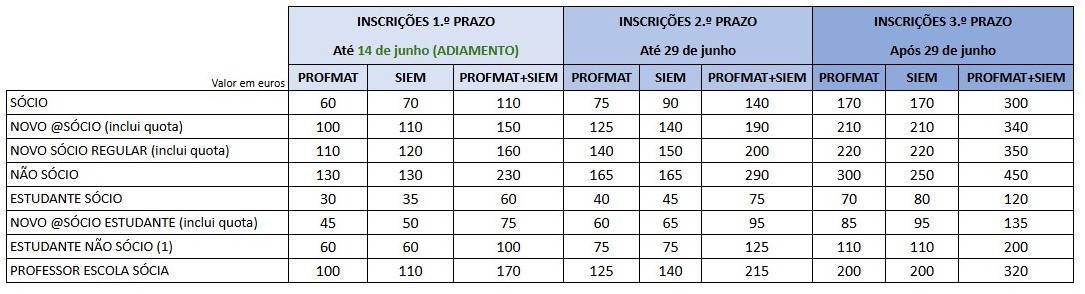
Na tabela acima, encontram-se os preços de inscrição para estes encontros, por prazo e situação do participante.
Data limite de devoluções
Até 23 de junho, as desistências são reembolsadas em 50% do valor pago. Após esta data, não há lugar a devoluções.
Inscrição
A inscrição no encontro ProfMat 2025 e/ou SIEM 2025 requer o preenchimento de um formulário de inscrição.
Após completar a sua inscrição, terminando com a submissão desse formulário, deve efetuar a transferência bancária referente ao valor total da sua inscrição (total da inscrição, incluindo jantar e/ou almoços caso selecione estas opções) para a conta da APM com o IBAN PT50003503250000664993010 e enviar comprovativo para centroformacao@apm.pt (logo após efetuar a sua inscrição).
No descritivo da transferência bancária, no caso dos associados da APM deve constar o número de sócio e/ou primeiro e último nome, no caso dos não sócios o primeiro e último nome.
A inscrição só fica concluída após o envio do comprovativo de pagamento.
Para se inscrever no ProfMat e/ou SIEM, clique no botão abaixo:
| Inscrição |



.png)








































 Letícia Gabriela Martins
Letícia Gabriela Martins 
 Cláudia Maria Canha Nunes Johnen Torres – Coordenadora do Projeto #EstudoEmCasa Apoia desde 2021 e professora de Quadro do Agrupamento de Escolas D. Dinis em Lisboa é Doutorada em Educação, na Área de especialização da Didática da Matemática, pela Instituto de Educação da Universidade de Lisboa, com a tese A liderança e a gestão curricular no contexto de um grupo de professores de matemática (2014), e professora de Matemática do 3.º ciclo do ensino básico e ensino secundário há 28 anos. Participou em diversos projetos de investigação nacionais (Membro da Equipa de Projeto de avaliação de Manuais escolares, Membro da Equipa de Projeto Mais Sucesso Escolar, tipologia híbrida; e, mais recentemente, o CRIarte - educação inclusiva e Ecossistemas de Aprendizagem e Bem-estar) e internacionais (PDTR – Professional Development of Teachers’ Researchers e LPS – Learning from Students perspective).
Cláudia Maria Canha Nunes Johnen Torres – Coordenadora do Projeto #EstudoEmCasa Apoia desde 2021 e professora de Quadro do Agrupamento de Escolas D. Dinis em Lisboa é Doutorada em Educação, na Área de especialização da Didática da Matemática, pela Instituto de Educação da Universidade de Lisboa, com a tese A liderança e a gestão curricular no contexto de um grupo de professores de matemática (2014), e professora de Matemática do 3.º ciclo do ensino básico e ensino secundário há 28 anos. Participou em diversos projetos de investigação nacionais (Membro da Equipa de Projeto de avaliação de Manuais escolares, Membro da Equipa de Projeto Mais Sucesso Escolar, tipologia híbrida; e, mais recentemente, o CRIarte - educação inclusiva e Ecossistemas de Aprendizagem e Bem-estar) e internacionais (PDTR – Professional Development of Teachers’ Researchers e LPS – Learning from Students perspective). 


















