PROFMAT e SIEM 2024 - Caldas da Rainha
XXXIX ProfMat e XXXIV SIEM
Em julho de 2024, as Caldas da Rainha recebem o ProfMat 2024 - XXXIX Encontro Nacional de Professores de Matemática (nos dias 15, 16 e 17), e o SIEM 2024 - XXXIV Seminário de Investigação em Educação Matemática (nos dias 17 e 18). Os encontros realizam-se na Escola Secundária Rafael Bordalo Pinheiro e no CCC - Centro Cultural e Congressos de Caldas da Rainha.
Na esperança de que nos possamos todos reencontrar, convidamos-vos a participar no ProfMat e no SIEM 2024.
PROGRAMA E RESUMOS
DISPENSA ESPECIAL DE SERVIÇO
Foi concedida dispensa especial de serviço nos dias 15, 16 e 17 de julho aos professores dos Grupos de Recrutamento 110, 230 e 500 para poderem participar no ProfMat 2024.
CALDAS DA RAINHA
Mapa:
Caldas da Rainha
Praça da República (Praça da Fruta)
Caldas da Rainha, também conhecida por "Termas da Rainha", foi procurada pela Rainha D. Leonor no séc. XV que ao usufruir das competências terapêuticas das águas termais viu sarada uma ferida que há muito não cicratizava, mesmo após os mais diversos tratamentos. A Rainha mandou então construir um hospital à volta do qual se formou a povoação que assim ficou conhecida como "Caldas da Rainha".
A cidade das Caldas da Rainha oferece um vasto conjunto de atrações turísticas. Descubra uma cidade que se orgulha de ser refúgio terapêutico e artístico. Eleita cidade criativa pela UNESCO.
 |
 |
 |
 |
 |
 |
ORGANIZAÇÃO
Os encontros de professores ProfMat e SIEM são organizados pela Associação de Professores de Matemática.
Em 2024, esta organização conta com a parceria da Câmara Municipal de Caldas da Rainha.
PROFMAT 2024 - Vídeo de apresentação
Cartaz do ProfMat e do SIEM 2024
Para esta edição do ProfMat e do SIEM, a APM promoveu um concurso de cartazes no qual participaram 109 alunos dos três Agrupamentos de Escolas das Caldas da Rainha.
Cartaz vencedor
Cartaz elaborado por:
António Fonseca e Duarte Augusto
Na categoria "Cartaz do ProfMat e do SIEM 2024", apresentam-se os cinco primeiros lugares:
| 1.º | 2.º | 3.º | 4.º | 5.º |
 |
 |
 |
 |
 |
Seguidamente, apresentam-se os premiados em cada categoria, por decisão do Júri do Concurso:
Premiados na categoria "A.E. Dom João II":
| 1.º Lugar | 2.º Lugar | 3.º Lugar |
 |
 |
 |
Premiados na categoria "A.E. Rafael Bordalo Pinheiro":
| 1.º Lugar | 2.º Lugar | 3.º Lugar |
 |
 |
 |
Premiados na categoria "A.E. Raul Proença":
| 1.º Lugar | 2.º Lugar | 3.º Lugar |
 |
 |
 |
Parabéns a todos os participantes!
Recordamos os 64 candidatos a "Cartaz ProfMat e SIEM 2024":
CARTAZES DO A.E. DOM JOÃO II
| 01. | 02. | 03. | 04. |
 |
 |
 |
 |
| 05. | 06. | 07. | 08. |
 |
 |
 |
 |
| 09. | 10. | 11. | 12. |
 |
 |
 |
 |
| 13. | 14. | 15. | 16. |
 |
 |
 |
 |
| 17. | 18. | 19. | 20. |
 |
 |
 |
 |
| 21. | |||
 |
 |
 |
 |
CARTAZES DO A. E. RAFAEL BORDALO PINHEIRO
| 22. | 23. | 24. | 25. |
 |
 |
 |
 |
| 26. | 27. | 28. | 29. |
 |
 |
 |
 |
| 30. | 31. | 32. | 33. |
 |
 |
 |
 |
| 34. | 35. | 36. | 37. |
 |
 |
 |
 |
| 38. | |||
 |
 |
 |
 |
CARTAZES DO A.E. RAUL PROENÇA
| 39. | 40. | 41. | 42. |
 |
 |
 |
 |
| 43. | 44. | 45. | 46. |
 |
 |
 |
 |
| 47. | 48. | 49. | 50. |
 |
 |
 |
 |
| 51. | 52. | 53. | 54. |
 |
 |
 |
 |
| 55. | 56. | 57. | 58. |
 |
 |
 |
 |
| 59. | 60. | 61. | 62. |
 |
 |
 |
 |
| 63. | 64. | ||
 |
 |
 |
 |
XXXIX ProfMat — Apresentação
O ProfMat, encontro nacional de professores de Matemática, é uma das principais iniciativas da Associação de Professores de Matemática. Desde 1985, professores de todos os níveis de ensino reúnem-se para apresentar, debater, analisar, refletir, partilhar e compartilhar ideias e experiências, questões e desafios. Este encontro anual é emblemático da APM, sendo um momento de participação, de união e de motivação para todos os seus sócios.
Em 1990, pela primeira vez, o ProfMat realizou-se numa escola secundária. Quem esteve presente recorda um ambiente que não poderia ter sido mais apropriado para um encontro de professores preocupados com a sua prática profissional. É precisamente nesse local, a Escola Secundária Rafael Bordalo Pinheiro, nas Caldas da Rainha, que o ProfMat regressa em 2024 para discutir as principais questões que marcam a atualidade da educação e do ensino da Matemática.
Comissões — ProfMat
COMISSÃO ORGANIZADORA - PROFMAT 2024
Dina Tavares
Dora Vaz Pinto
Inês Silva
Joana Domingos
Joaquim Pinto
Lídia Oliveira
Manuel João Marques
Maria Fernanda Barros
Nádia Ferreira
Pedro Mesquita
Ricardo Vicente
COMISSÃO DO PROGRAMA - PROFMAT 2024
Alexandra Rodrigues
António Fernandes
Dina Tavares
Hélder Martins
Jaime Carvalho e Silva
Joaquim Pinto
Manuel João Marques
Paula Teixeira
Locais do ProfMat 2024
O ProfMat 2024 decorre nas Caldas da Rainha, mais especificamente em dois locais:
CENTRO CULTURAL E CONGRESSOS DE CALDAS DA RAINHA (CCC)
Mapa:
Rua Dr. Leonel Sotto Mayor 23D, 2500-227 Caldas da Rainha
Tlf: 262 094 081
Email: bilheteira@ccc.com.pt
URL: https://ccc.com.pt
 |
 |
 |
 |
ESCOLA SECUNDÁRIA RAFAEL BORDALO PINHEIRO (ESRBP)
Mapa:
Rua Almirante Gago Coutinho 1, 2500-000 Caldas da Rainha
Tlf: 262 870 070
Email: esrbp@esrbp.pt
URL: https://aerbp.pt
 |
 |
 |
 |
MAPA DA ZONA ENVOLVENTE

MAPA DA E. S. RAFAEL BORDALO PINHEIRO
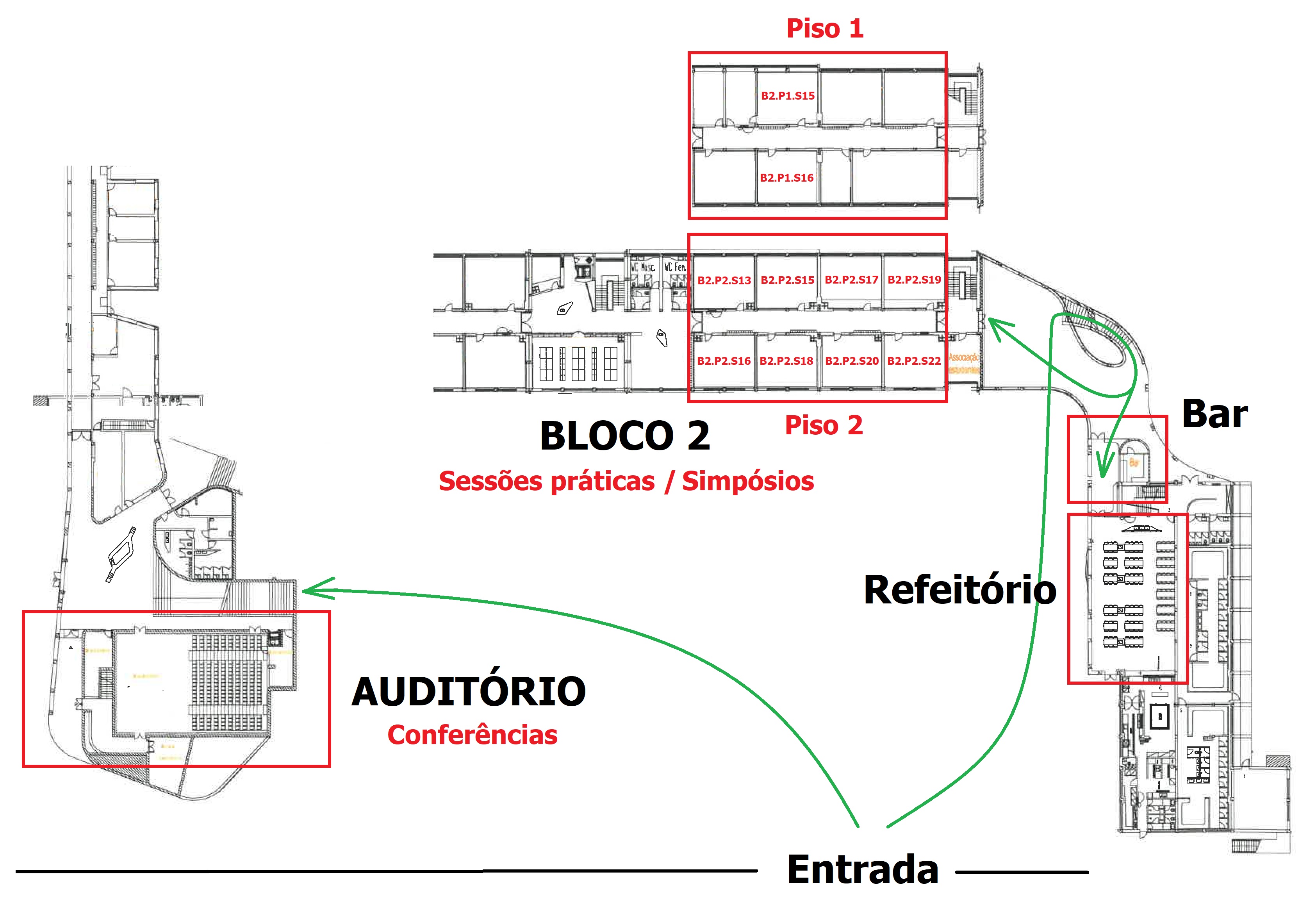
Programa ProfMat 2024

Programa Geral do ProfMat2024 em pdf
Almoços | Jantar do ProfMat
Almoços - 15, 16 e 17 de julho
Durante o ProfMat 2024, terá a possibilidade de almoçar no refeitório da E. S. Rafael Bordalo Pinheiro (pão, sopa, prato, salada, sobremesa e bebida). A inscrição num almoço e a respetiva escolha do prato (carne, peixe ou vegetariano) realiza-se através do formulário de inscrição no ProfMat 2024.
Cada almoço tem um custo de 8 euros, pago no ato de inscrição.
SEGUNDA-FEIRA, 15 DE JULHO
| Sopa | Creme de agrião |
| Prato de Carne | Bifinhos de porco com molho de cogumelos acompanhados com massa espiral |
| Prato de Peixe | Bacalhau espiritual |
| Prato Vegetariano | Legumes à brás |
| Sobremesa | Arroz doce ou fruta da época |
TERÇA-FEIRA, 16 DE JULHO
| Sopa | Camponesa |
| Prato de Carne | Strogonoff de perú com puré de batata e cenoura |
| Prato de Peixe | Perca no forno com crosta de broa e arroz de milho e ervilhas |
| Prato Vegetariano | Crepes de legumes com arroz branco |
| Sobremesa | Torta de laranja ou fruta da época |
QUARTA-FEIRA, 17 DE JULHO
| Sopa | Caldo verde |
| Prato de Carne | Carne de porco assada com massa esparguete e legumes salteados |
| Prato de Peixe | Salada russa de salmão |
| Prato Vegetariano | Rolinhos salsicha de tofu com lombardo com puré de batata |
| Sobremesa | Pudim de ovos ou fruta da época |
Jantar do ProfMat 2024 - Terça-feira 16 de julho
RESTAURANTE "A LAREIRA"
>
Mapa:
Rua da Lareira, n.º 35 Alto do Nobre - Nadadouro, Caldas da Rainha 2500-593
Tlf: 262 823 432
URL: https://www.restaurantealareira.com/
 |
 |
 |
 |
 |
 |
 |
 |
EMENTA
Couvert
Pão e Manteiga
Salada de Feijão Frade com Atum
Peixinhos da Horta
Fofinhos de Camarão
Queijo saloio fatiado
Presunto Serrano fatiado
Mini Rissóis de Peixe
Mini Croquetes de Carne
Mini Pasteis de Bacalhau
Sopa
Sopa de Espinafres com Farinheira da Beira
Alternativa Vegetariana: Creme de Alho Francês
Carne
Lombo de Porco recheado com Alheira de Mirandela servido com puré de batata, couve-flor gratinada, cenouras e castanhas caramelizadas
Alternativa Vegetariana: Canelloni de Espinafres com Cogumelo e Courgette servido com puré de batata, couve-flor gratinada, cenouras e castanhas caramelizadas
Sobremesa
Abacaxi flamejado à Lareira, servido com gelado de baunilha
Café
Cave
Vinho branco Lareira
Vinho tinto Lareira
Água
Cerveja
Sumo de Laranja
Preço por pessoa: 20,00 €
Alojamentos com protocolo
Nas Caldas da Rainha, bem como nas proximidades, encontram-se várias opções de alojamento. Seguidamente, apresentam-se algumas destas opções. As tarifas indicadas foram comunicadas à Comissão Organizadora do ProfMat pelos respetivos alojamentos.
HOTEL CRISTAL CALDAS ***
O Hotel Cristal Caldas está localizado bem no centro da cidade termal das Caldas da Rainha (a 650 metros do Centro Cultural e de Congressos) e a apenas 7 km da Praia Foz de Arelho. O hotel possui 113 quartos e uma piscina exterior.
 |
 |
Localização - R. António Sérgio 31, 2500-130 Caldas da Rainha
Telefone - 262 840 260
Email - booking3@hoteiscristal.pt
Website - https://www.hoteiscristal.pt/cristal-caldas/
Tarifas de alojamento, por noite, por quarto:
Single - 66,00 € - 55,00 €
Duplo - 73,00 € - 65,00 €
Com pequeno-almoço buffet incluído
Nota: As reservas deverão ser efetuadas por email ou telefone e deverão mencionar que são participantes no ProfMat.
SANA SILVER COAST HOTEL ****
Em pleno centro das Caldas da Rainha, o SANA Silver Coast Hotel dá uma nova alma a um antigo edifício do século XIX, que em tempos foi o Grande Hotel Lisbonense. Num ambiente de charme e elegância descubra todas as surpresas que as Caldas da Rainha têm para oferecer.
 |
 |
Localização - Av. Dr. Manuel Figueira Freire da Câmara, 2500-184 Caldas da Rainha
Telefone - 262 000 600
Email - sanasilvercoast@sanahotels.com
Website - https://www.sanahotels.com/pt/hotel/sana-silver-coast/
Tarifas de alojamento, por noite, por quarto:
Single - 100 € - 89 €
Duplo - 115 € - 99 €
Com pequeno-almoço incluído, estacionamento Gratuito + 10% desconto em F&B
Nota: As reservas deverão ser efetuadas por email ou telefone e deverão mencionar que são participantes no ProfMat.
CALDAS INTERNACIONAL HOTEL ***
Situado a 900 metros do Centro Cultural e de Congressos das Caldas da Rainha, o Hotel Caldas Internacional dispõe de quartos espaçosos, de uma piscina exterior e ainda de estacionamento gratuito para os hóspedes.
 |
 |
Localização - Rua Dr. Artur Figueirôa Rêgo, 45, Caldas da Rainha
Telefone - 262 830 500
Email - info@caldasinternacionalhotel.com
Website - caldasinternacionalhotel.com
Tarifas de alojamento, por noite, por quarto:
Single - 65,00 € - 55,00€
Duplo/twin - 75,00 € - 65,00€
Com pequeno-almoço continental/buffet incluído
Nota: As reservas deverão ser efetuadas por email ou telefone e deverão mencionar que são participantes no ProfMat.
NOVA DELPA AL ***
O Nova Delpa AL é um pequeno “hotel” localizado no centro das Caldas da Rainha, junto à Praça da Fruta, às termas, ao Parque D. Carlos I e à rua comercial. Os pontos turísticos mais importantes da cidade ficam a 5 minutos a pé do Nova Delpa AL.
 |
 |
Localização - R. Emídio de Jesus Coelho 20, 2500-198 Caldas da Rainha
Telefone - 916 962 404
Email - novadelpa@gmail.com
Website - https://www.novadelpa.pt
Tarifas de alojamento, por noite, por quarto:
Quartos duplos - Desconto sobre os preços apresentados no booking
Nota: As reservas deverão ser efetuadas por email ou telefone e deverão mencionar que são participantes no ProfMat.
HOTEL VILA D'ÓBIDOS ****
Situado a 5 km das Caldas da Rainha, o Hotel Vila D'Óbidos apresenta uma arquitetura de estilo contemporâneo, conseguindo uma harmonia total com o ambiente natural nos 6 hectares da Quinta de Santo Antão. Dispõe de 40 quartos decorados com obras de artistas portugueses.
 |
 |
Localização - Quinta Santo Antão Estrada Nossa Senhora da Luz, 2510-192 Óbidos
Telefone - 262 003 100
Email - geral@hotelviladobidos.pt
Website - www.hotelviladobidos.pt
Alojamento
10% de desconto sobre o valor do site
Pequeno-almoço incluído
Acesso ao Centro de Bem-Estar (piscina interior, sauna e banho turco) mediante marcação prévia.
Duas tipologias de quartos disponíveis:
- Quartos Standard com acesso apenas por escadas para 1.º ou 2.º piso, sem vista piscina/castelo;
- Quartos Deluxe, com varanda, com acesso por elevador e vista piscina/castelo.
Pagamento a efetuar no Check-In
Nota: As tarifas são variáveis, pelo que, se os participantes fizerem reservas em alturas diferentes poderão ter tarifas diferentes.
Para efetuarem as reservas, terão que se identificar como participantes do ProfMat.
EUROPEIA HOTEL ***
Este hotel desfruta de uma localização central nas Caldas da Rainha, no interior do Centro Comercial Rua das Montras. Está a poucos metros do mercado tradicional "Praça da Fruta" e do Centro Cultural de Congressos.
 |
 |
Localização - R. Alm. Cândido Reis 64, 2500-125 Caldas da Rainha
Telefone - 961 775 165 | 262 839 320
Email - europeiahotel@gmail.com
Facebook - Europeia Hotel
Tarifas de alojamento, por noite, por quarto:
Single - 55,00 € - 50,00€
Duplo/twin - 65,00 € - 60,00€
Com pequeno-almoço incluído
Nota: As reservas deverão ser efetuadas por email ou telefone e deverão mencionar que são participantes no ProfMat.
HOTEL ÁGUA D'ALMA ***
O Água d’Alma Hotel situa-se na Foz do Arelho, junto à Lagoa de Óbidos, uma pequena vila a 8 km da cidade de Caldas da Rainha. A água é um elemento intrinsecamente ligado ao hotel; a alma vem da ideia de leveza, tranquilidade e paz, conceitos fortes que têm passado pelas três gerações da família que gere o hotel.
 |
 |
Localização - R. dos Camarções 3, 2500-481 Foz do Arelho
Telefone - 262 979 610
Email - geral@aguadalma.pt
Website - https://www.aguadalma.pt/
Vídeo de apresentação - YouTube
Alojamento
10% de desconto entre 14 e 18 de julho
Basta que os participantes insiram o código promocional "profmat2024" no motor de reservas do site para acederem à tarifa com desconto.
Submissão de Comunicações e Sessões Práticas
Os participantes no ProfMat podem submeter propostas de comunicações e sessões práticas.
As propostas devem seguir as indicações dos respetivos modelos e serem enviadas até 19 de maio, através dos formulários abaixo.
A notificação acerca da aceitação da proposta será enviada até 05 de junho.
COMUNICAÇÃO EM SIMPÓSIO
As comunicações para os simpósios são propostas e dinamizadas por participantes no encontro, fundamentalmente sobre temas e abordagens de ensino e materiais didáticos. Cada comunicação tem a duração de 15 minutos e está integrada num simpósio de comunicações, reservando-se, no final do respetivo simpósio, 15 minutos para discussão coletiva.
Modelo para submissão de Comunicação
| Submissão de Comunicação |
SESSÃO PRÁTICA
As sessões práticas são propostas e dinamizadas por participantes no encontro, fundamentalmente sobre temas e abordagens de ensino e materiais didáticos. Cada sessão prática tem a duração de 120 minutos.
Modelo para submissão de Sessão Prática
| Submissão de Sessão Prática |
Modelo de PowerPoint
Se vai apresentar alguma comunicação ou sessão prática e pretende utilizar um modelo comum, próprio deste ProfMat, descarregue-o aqui:
Acreditação
FORMAÇÃO
O “39.º Encontro Nacional de Professores de Matemática — ProfMat 2024” é um curso de formação de 15 horas acreditado pelo CCPFC para os grupos 110, 230 e 500 (CCPFC/ACC-126536/24) na dimensão científica e pedagógica.
Os docentes que tiveram assiduidade e receberam e-mail do Centro de Formação, para obter certificação, devem:
- Enviar, para o endereço de correio eletrónico do CFAPM, centroformacao@apm.pt, o relatório de reflexão crítica individual até dia 31/07/2024. O envio do relatório até à data indicada é da exclusiva responsabilidade do formando, não sendo aceites relatórios entregues depois de 31/07/2024. O Centro de Formação responde a todos os e-mails. Caso não seja confirmada a receção do seu relatório, volte a contactar o Centro de Formação.
- Para a realização do relatório de reflexão crítica individual, utilizar o documento enviado em anexo pelo Centro de Formação APM e disponível também no site do encontro encontro no menu Acreditação: https://www.apm.pt/profmat2024.
- Preencher, até ao dia 31/07/2024, o questionário de avaliação da ação disponível no link: https://forms.gle/8WTJ4VpfxiHsZQZZ7
- Contactar o CFAPM (centroformacao@apm.pt) para qualquer questão relacionada com o processo de acreditação.
AVALIAÇÃO DOS FORMANDOS
A avaliação é individual e traduz-se numa classificação final quantitativa, na escala de 1 a 10, expressa através do referencial de menções qualitativas previsto no n.º 2 do artigo 46.º do ECD aprovado pelo Decreto-Lei n.º 15/2007, de acordo com as seguintes ponderações:
Assiduidade – 40%
Relatório de reflexão crítica individual – 60%
ASSIDUIDADE
A assiduidade é comprovada através da assinatura de folha de registo de presença. Os formandos que não participem em pelo menos dois terços (10 horas) do número total de horas de formação (15 horas) não poderão obter aprovação. A assinatura das folhas de registo de presença, é da responsabilidade de cada formando.
RELATÓRIO DE REFLEXÃO CRÍTICA INDIVIDUAL
O relatório de reflexão crítica individual incidirá sobre a globalidade da temática do encontro, numa perspetiva global, integradora e sistemática, sendo liminarmente excluídos trabalhos que não respeitem esta condição ou não se enquadrem nas regras definidas.
A avaliação do relatório de reflexão crítica individual será realizada de acordo com um conjunto de descritores:
O relatório terá de ser redigido em documento digital (sugerimos o envio do trabalho em formato pdf) e gravado com o seguinte nome: (Nome_do_docente_grupo disciplinar)_ProfMat2024:
- Número mínimo de páginas: 1
- Número máximo de páginas: 3 (sem contabilizar a capa)
- Margens: superior 2,5 cm, inferior 2,5 cm, lateral esquerda 3 cm, lateral direita 3 cm
- Fonte: Arial, tamanho12, espaçamento 1,15
A avaliação final terá uma menção qualitativa (Insuficiente, Regular, Bom, Muito Bom e Excelente) e o valor final da classificação quantitativa, numa escala de 1 a 10. A acreditação da formação depende da obtenção da classificação mínima de cinco valores, na escala de 1 a 10.
CERTIFICAÇÃO DE FORMAÇÃO ACREDITADA
Para os formandos que cumpram todas as formalidades da formação acreditada, frequentem, pelo menos, dois terços do número total de horas do curso de formação e sejam aprovados, será emitido um Certificado de Formação.
A Pauta de Avaliação estará disponível na APM. Os certificados referentes à formação serão enviados, via e-mail, pelo Centro de Formação para cada um dos formandos aprovados a partir de setembro/outubro de 2024.
Contactos
profmat2024@apm.pt
ProfMat 2024 - Associação de Professores de Matemática
Rua Dr. João Couto, n.º 27-A
1500-236 Lisboa
Tel.: +351 21 716 36 90 / 21 711 03 77
 |
 |
 |
 |
Materiais — ProfMat 2024
Os materiais que forem cedidos pelos conferencistas serão disponibilizados aqui, logo que nos forem enviado e/ou depois da realização do ProfMat.
ProfMat 2024 - Conferências Plenárias (1h)
As conferências plenárias são realizadas por pessoas convidadas pela organização e com reconhecida experiência na área em que vão intervir. Incidem sobre temas de interesse geral e realizam-se em espaços do programa de forma a que todos os participantes tenham possibilidades de assistir.
CP 01 - Trilhos matemáticos: apontamentos sobre a construção, potencialidades e desafiosFátima Fernandes, Escola Superior de Educação de Viana do Castelo Moderador: Eduardo Cunha Segunda-feira, 15 de julho, 12h00m - 13h00m Resumo Nesta conferência será evidenciado o trilho matemático enquanto estratégia de ensino e aprendizagem da matemática e de criação de conexões com outras áreas do conhecimento. Após um breve enquadramento, procurar-se-á destacar alguns aspetos que se consideram relevantes no processo de construção de um trilho em suporte de papel ou envolvendo a tecnologia, aspetos estes relacionados com os contextos e com a formulação e resolução das tarefas. Serão enfatizadas algumas potencialidades desta abordagem da matemática fora da sala de aula para o ensino e aprendizagem relacionadas com diferentes domínios, nomeadamente o domínio cognitivo, o físico/motor, o social e o afetivo. Serão ainda apontadas algumas recomendações, necessidades e limitações inerentes aos trilhos com orientações e resoluções em papel e em versão digital. Nota biográfica
Fátima Fernandes – Professora Adjunta na Escola Superior de Educação do Instituto Politécnico de Viana do Castelo, onde exerce funções docentes desde 2006 em cursos ligados à formação inicial e contínua de professores. |
CP 02 - O PASEO, 7 anos depoisGuilherme d’Oliveira Martins, Coordenador do Perfil dos Alunos à Saída da Escolaridade Obrigatória (PASEO) Moderador: Joaquim Pinto Segunda-feira, 15 de julho, 15h00m - 16h00m Resumo A educação para todos consagrada como primeiro objetivo mundial da UNESCO obriga à consideração da diversidade e da complexidade como fatores a ter em conta ao definir o que se pretende para a aprendizagem dos alunos à saída dos 12 anos de escolaridade obrigatória. A referência a um perfil não visa, porém, qualquer tentativa uniformizadora, mas sim criar um quadro de referência que pressuponha a liberdade, a responsabilidade, a valorização do trabalho, a consciência de si próprio, a inserção familiar e comunitária e a participação na sociedade que nos rodeia. Nota biográfica
Guilherme d’Oliveira Martins (n. Lisboa, 1952) – Administrador Executivo da Fundação Calouste Gulbenkian e Presidente do Grande Conselho do Centro Nacional de Cultura. Licenciado e Mestre em Direito. Professor Universitário Convidado. Doutor Honoris Causa pela Universidade Lusíada, pela Universidade Aberta e pela Universidade de Lisboa (ISCSP). Sócio Correspondente da Academia Brasileira de Letras – Cadeira 20. Presidente da Assembleia Geral da World Monuments Fund (1.06.2023). Presidente do Conselho Consultivo do Banco Português do Fomento (2024). Foi Presidente do Conselho Fiscal da Caixa Geral de Depósitos, S.A. (2016-2021). Foi Presidente do Tribunal de Contas (2005-2015). Nos Governos de Portugal foi, sucessivamente, Secretário de Estado da Administração Educativa (1995-1999), Ministro da Educação (1999-2000), Ministro da Presidência (2000-2002) e Ministro das Finanças (2001-2002). Foi Presidente da SEDES - Associação para o Desenvolvimento Económico e Social (1985-1995) e Vice-Presidente da Comissão Nacional da UNESCO (1988-1994). Foi Presidente da Comissão do Conselho da Europa que elaborou a Convenção de Faro sobre o valor do Património Cultural na sociedade contemporânea [Faro, (Portugal) 27 de outubro de 2005]. Foi Presidente da EUROSAI – Organização das Instituições Superiores de Controlo das Finanças Públicas da Europa (2011-2014) e Presidente do Conselho de Prevenção da Corrupção (2008-2015). Foi Coordenador Nacional do Ano Europeu do Património Cultural 2018. |
CP 03 - Problemas fáceis, resoluções difíceis (e vice-versa)José Paulo Viana, APM Moderador: Paulo Correia Segunda-feira, 15 de julho, 17h30m - 18h30m Resumo Os problemas preferidos por muita gente têm quase sempre um enunciado fácil e depois uma resolução difícil, ou engenhosa, ou as duas coisas ao mesmo tempo. Há também problemas em que, depois de lermos o enunciado, pensamos: “Aqui está um difícil”. Andamos às voltas com ele e de repente descobrimos que existe um processo fácil de chegar à solução. Temos ainda problemas que nos abrem novos horizontes e nos fazem descobrir muito mais do que aquilo que inicialmente estávamos à espera. Irei falar um pouco destes problemas, com alguns dos exemplos de que mais gosto: Nota biográfica
José Paulo Viana – Professor de Matemática do ensino secundário (aposentado). Entusiasta das matemáticas recreativas e da Magia Matemática. Autor, durante mais de 28 anos, da secção semanal “Desafios” no jornal Público. Em 2014 foi-lhe atribuído o Prémio Ciência Viva nos Media. Divulgador de Matemática através de conferências e sessões em escolas e em locais públicos. Autor de manuais escolares e dos livros de divulgação matemática e de matemáticas recreativas “Uma Vida Sem Problemas”, “Problemas… Sem Problema” e “Desafios” (10 volumes). |
CP 04 - Estratégias para despertar o interesse pela GeometriaMaria Manuel Torres, Faculdade de Ciências da ULisboa Moderador: João Almiro Terça-feira, 16 de julho, 16h30m - 17h30m Resumo A Geometria é a forma mais primitiva de conhecimento humano, desde a mais tenra infância que todos sabemos reconhecer círculos, quadrados ou triângulos. Quando uma criança começa a desenhar, cria formas geométricas: curvas, linhas, pontos... Mas a partir de uma certa altura, começamos a ouvir frases como: Não gosto de geometria, não tem interesse, não percebo qual é a utilidade. Muitas vezes, a geometria não é sequer associada à própria matemática. Nota biográfica
Maria Manuel Torres – Licenciada em Matemática, plea Universidade de Perugia (Itália). |
ProfMat 2024 - Painel Plenário (2h)
Sessão especialmente organizada para promover uma discussão sobre um tema de atualidade, com vários intervenientes convidados para o efeito. É preparada e conduzida por um moderador convidado pela organização que solicita intervenções dos vários participantes do painel sobre o tema em discussão e em resposta a questões da assistência que em momento próprio é convidada a intervir.
Desafios de sempre na aprendizagem e no ensino da Matemática: Contributos de Leonor SantosModeradora: Ana Paula Canavarro, Universidade de Évora Intervenientes: Paula Teixeira, Projeto MAT 789 Quarta-feira, 17 de julho, 11h30m - 13h00m Resumo Quando nos referimos à aprendizagem e ao ensino da Matemática, uma das ideias que imediatamente surge é a de complexidade, de um contexto de trabalho difícil, onde são múltiplos os problemas a enfrentar, e onde existem desafios que perduram no tempo. Leonor Santos conceptualizou a atividade do professor como uma atividade permanente de resolução de problemas e (e)laborou sobre diversas ideias que constituem desafios de sempre, procurando responder-lhes com propostas efetivas de trabalho que foram além de teoria e se desenvolveram na(s) prática(s). Neste painel, procuramos sistematizar e destacar ideias-chave do seu trabalho em prol da qualidade da aprendizagem e do ensino da Matemática, através de testemunhos de quem trabalhou em diversos contextos profissionais, numa homenagem a esta profissional de valor ímpar cuja obra marcou a evolução dos caminhos da educação matemática em Portugal – e que nos continuará sempre a inspirar. |
ProfMat 2024 - Conferências com Discussão (1h)
As conferências com discussão são intervenções realizadas por pessoas convidadas pela organização para intervir em áreas ou temas considerados de interesse para os participantes. Incidem sobre assuntos diversificados e são seguidas de um espaço de discussão com os presentes, com um moderador convidado para o efeito.
|
CD 01 |
Geometria Analítica e Sintética e Ambientes de Geometria Dinâmica (AGD) (Resumo) João Almiro, APM Público: SECUNDÁRIO |
Terça-feira, 16 de julho 9h00 - 10h00 |
Grande Auditório do CCC |
|
CD 02 |
Educação matemática com recurso a narrativas infantojuvenis (Resumo) Susana Colaço | Maria Clara Martins Público: 1.º CICLO e 2.º CICLO |
Quarta-feira, 17 de julho 10h00 - 11h00 |
Auditório da ESRBP |
|
CD 03 |
Modelação Matemática e Currículo CTEAM: Reflexões sobre o Passado e sobre o Futuro (Resumo) Vítor Duarte Teodoro, Universidade Lusófona | Universidade Nova de Lisboa Público: GERAL |
Segunda-feira, 15 de julho 16h00 - 17h00 |
Pequeno Auditório do CCC |
|
CD 04 |
Ensinar e Aprender com Tecnologias Digitais no 1.º Ciclo do Ensino Básico (Resumo) Joaquim Escola, Universidade de Trás-os-Montes e Alto Douro Público: 1.º CICLO |
Terça-feira, 16 de julho 14h00 - 15h00 |
Grande Auditório do CCC |
|
CD 05 |
Discalculia e Baixo Rendimento a Matemática na Sociedade Atual (Resumo) Lília Marcelino, CeiED – Universidade Lusófona Público: GERAL |
Terça-feira, 16 de julho 14h00 - 15h00 |
Auditório da ESRBP |
|
CD 06 |
Tópicos de Matemática e Arte – uma experiência pedagógica (Resumo) Pedro Freitas, Faculdade de Ciências da Universidade de Lisboa Público: GERAL |
Terça-feira, 16 de julho 10h00 - 11h00 |
Pequeno Auditório do CCC |
| CD 07 |
Novas Aprendizagens Essenciais de Matemática B: A experiência numa turma-piloto (Resumo) Pedro Liberto Ferreira | Sandra Afonso Público: SECUNDÁRIO |
Terça-feira, 16 de julho 11h30 - 12h30 |
Auditório da ESRBP |
| CD 08 |
Os caminhos e desafios da avaliação externa digital: condição necessária ou suficiente? (Resumo) Luís Pereira dos Santos, Instituto de Avaliação Educativa, I.P. Público: GERAL |
Segunda-feira, 15 de julho 16h00 - 17h00 |
Grande Auditório do CCC |
| CD 09 |
A matemática nos estudos internacionais da OCDE: PISA, PISA-VET e PIAAC (Resumo) Anabela Serrão, Instituto de Avaliação Educativa, I.P. Público: SECUNDÁRIO |
Quarta-feira, 17 de julho 10h00 - 11h00 |
Pequeno Auditório do CCC |
| CD 10 |
Matemática Computacional: um convite à Matemática (Resumo) Carlos Albuquerque, Faculdade de Ciências, Universidade de Lisboa Público: 3.º CICLO e SECUNDÁRIO |
Terça-feira, 16 de julho 10h00 - 11h00 |
Grande Auditório do CCC |
| CD 11 |
Percursos que contam em Quarteira (Resumo) Nélida Filipe, Agrupamento de escolas Dra. Laura Ayres Público: GERAL |
Terça-feira, 16 de julho 11h30 - 12h30 |
Grande Auditório do CCC |
| CD 12 |
Ensino Profissional e as Novas Aprendizagens do Ensino da Matemática (Resumo) Cristina Fernandes, Agrupamento de Escolas de Sampaio Público: SECUNDÁRIO |
Terça-feira, 16 de julho 11h30 - 12h30 |
Pequeno Auditório do CCC |
| CD 13 |
Promover práticas de pensamento computacional no ensino da matemática nos 1.º e 2.º Ciclos do Ensino Básico (Resumo) Rui Gonçalo Espadeiro, Agrupamento de Escolas de Redondo Público: 1.º CICLO e 2.º CICLO |
Segunda-feira, 15 de julho 16h00 - 17h00 |
Auditório da ESRBP |
| CD 14 |
Pensamento estatístico: a importância decisiva do contexto (Resumo) Susana Carreira, Universidade do Algarve Público: SECUNDÁRIO |
Quarta-feira, 17 de julho 10h00 - 11h00 |
Grande Auditório do CCC |
| CD 15 |
Modelos matemáticos em finanças nas novas Aprendizagens Essenciais de Matemática (Resumo) Helder Martins, Escola Secundária António Damásio, Lisboa Público: SECUNDÁRIO |
Terça-feira, 16 de julho 9h00 - 10h00 |
Pequeno Auditório do CCC |
| CD 16 |
Os manuais e as novas Aprendizagens Essenciais de Matemática no Ensino Profissional (Resumo) Maria Augusta Ferreira Neves | Bruno Roque | Pedro Rocha Almeida Público: SECUNDÁRIO PROFISSIONAL |
Terça-feira, 16 de julho 14h00 - 15h00 |
Pequeno Auditório do CCC |
| CD 17 |
A aprendizagem da Matemática em atividades STEAM nos 1.º e 2.º ciclos do ensino básico (Resumo) Neusa Branco, ESE de Santarém | Polo de Literacia Digital e Inclusão Social, CIAC, UAlg Público: 1.º e 2.º CICLOS |
Terça-feira, 16 de julho 9h00 - 10h00 |
Auditório da ESRBP |
| CD 18 |
Dados nos primeiros anos…quais as novidades?! (Resumo) Ana Caseiro, Escola Superior de Educação de Lisboa Público: 1.º CICLO |
Terça-feira, 16 de julho 10h00 - 11h00 |
Auditório da ESRBP |
RESUMOS
CD 01 - Geometria Analítica e Sintética e Ambientes de Geometria Dinâmica (AGD)João Almiro, APM | Paulo Correia, Escola Secundária de Alcácer do Sal Moderador: Rui Gonçalo Espadeiro Terça-feira, 16 de julho, 9h00m - 10h00m Resumo O recurso a Ambientes de Geometria Dinâmica (AGD) no plano e no espaço faz-nos refletir sobre como devem ser as aulas em que se leciona Geometria, quando os AGD estão regularmente presentes e de forma significativa. Partimos do princípio que os alunos devem ser capazes de interpretar e produzir diferentes representações (geométricas, numéricas e algébricas) dos conceitos em estudo, mas explorando todas as potencialidades da tecnologia agora disponível. nesta conferência tentaremos discutir os problemas que se colocam à concretização plena desta abordagem, discutindo o papel das representações geométricas, da Álgebra, das generalizações e do raciocínio dedutivo e a importância da criação e adaptação de tarefas que permitam desenvolver as competências visadas nas novas Aprendizagens Essenciais. Finalmente, gostaríamos que esta sessão suscitasse a partilha de reflexões e de questões entre todos os presentes sobre esta problemática. Notas biográficas
João Almiro – Licenciado em Matemática – Ramo Educacional e Mestre em Educação – Didáctica de Matemática na Faculdade de Ciências da Universidade de Lisboa. Foi professor de Matemática na Escola Secundária de Tondela, tendo estado envolvido em vários programas de formação tanto em Centros de Formação de Associação de Escolas, como em colaboração com o Ministério da Educação e a APM. Integrou os grupos de trabalho que redigiram as "Recomendações para a melhoria das aprendizagens dos alunos em Matemática" e as Aprendizagens Essenciais de Matemática para o Ensino Secundário.
Paulo Correia – Licenciado em Ensino de Matemática na Universidade de Évora, onde também concluiu o Curso de Especialização em Educação Matemática. É professor de Matemática do Ensino Básico e Secundário na Escola de Alcácer do Sal e desenvolve atividade como formador. Integrou os Grupos de Trabalho que redigiram as "Recomendações para a melhoria das aprendizagens dos alunos em Matemática", as Aprendizagens Essenciais de Matemática para o Ensino Básico e para o Ensino Secundário. Mantém a página https://mat.absolutamente.net |
CD 02 - Educação matemática com recurso a narrativas infantojuvenisSusana Colaço | Maria Clara Martins Moderadora: Renata Carvalho Quarta-feira, 17 de julho, 10h00m - 11h00m Resumo Esta conferência visa apresentar a utilização de narrativas infantojuvenis como um recurso valioso na formação de professores dos primeiros anos (1.º e 2.º CEB) no âmbito da educação matemática. As narrativas, pelo conteúdo explícito ou pelas ideias ou conceitos subliminares que apresentam podem representar um ponto de partida para a articulação entre várias áreas do conhecimento, promovendo não apenas o desenvolvimento do conhecimento da língua portuguesa, mas também o conhecimento de outras áreas do saber, neste caso da Matemática. Apresentamos algumas experiências na formação inicial de educadores e professores dos primeiros anos aliadas às didáticas específicas ou integradas em contextos de prática de ensino supervisionada no 1º CEB. Procuraremos mostrar, e depois discutir, as potencialidades da articulação realizada: de que forma esta contribui para o desenvolvimento do conhecimento pedagógico dos futuros professores e que vantagens existem em continuar a aliar a literatura infantojuvenil à matemática para o desenvolvimento de aprendizagens dos alunos. Notas biográficas
Susana Colaço – Licenciada, mestre e doutorada em Matemática e especialista em formação de professores do ensino básico (1.º e 2.º CEB). Foi diretora da ESE-IPSantarém durante 4 anos (2018-2022). É coordenadora do mestrado em Educação Pré-Escolar e Ensino do 1.º CEB e do Departamento de ciências matemáticas e naturais da ESE. Há mais de 25 anos é formadora de professores e educadores, quer no âmbito da formação inicial, quer na formação contínua. Tem participado em vários projetos financiados de investigação e desenvolvimento relacionados com a formação inicial e contínua de professores.
|
CD 03 - Modelação Matemática e Currículo CTEAM: Reflexões sobre o Passado e sobre o FuturoVítor Duarte Teodoro, Universidade Lusófona | Universidade Nova de Lisboa Moderador: Helder Martins Segunda-feira, 15 de julho, 16h00m - 17h00m Resumo Nas últimas décadas, termos como “modelação”, “múltiplas representações”, “pensamento computacional” têm vindo a adquirir progressivamente maior importância no currículo (em todos os níveis) da Matemática e das restantes CTEAM (disciplinas de Ciências, Tecnologias, Engenharias, Artes, e Matemática). Esta mudança foi influenciada por mudanças tecnológicas mas também por mudanças conceptuais sobre a natureza e práticas das CTEAM e dos respectivos processos de aprendizagem e de ensino. Nesta conferência, discutem-se algumas dessas mudanças, com base em exemplos, faz-se uma análise de alguns currículos CTEAM das últimas décadas, exploram-se ferramentas de modelação matemática e discute-se que implicações têm sobre as práticas escolares nas diversas disciplinas, numa perspectiva integrada, no futuro… e no presente. Nota biográfica
Vítor Duarte Teodoro – Professor do Instituto de Educação da Universidade Lusófona, Lisboa. Professor aposentado da FCT da Universidade Nova de Lisboa. Professor do Ensino Básico e Secundário (FQ e Matemática) entre 1974 e 1985. Autor de software educativo para CTEAM, de manuais escolares e de livros sobre educação e ensino, bem como de estudos sobre currículo, exames, tecnologias, etc. Para mais informação, ver https://www.cienciavitae.pt/portal/2A19-1E93-4EC2. |
CD 04 - Ensinar e Aprender com Tecnologias Digitais no 1.º Ciclo do Ensino BásicoJoaquim Escola, Universidade de Trás-os-Montes e Alto Douro Moderador: Manuel Vara Pires Terça-feira, 16 de julho, 14h00m - 15h00m Resumo O ensino tem vindo a sofrer alterações profundas. O desenvolvimento tecnológico e científico a par das transformações sofridas decorrentes da pandemia, criaram condições adequadas para uma reflexão aprofundada acerca da integração curricular das tecnologias digitais da informação e comunicação em todos os níveis de ensino, de modo particular nos primeiros níveis de ensino. Estas profundas transformações têm proporcionado novas possibilidades de organizar os processos comunicacionais nos contextos de ensino, cada vez mais exigentes e, naturalmente, mais desafiantes.
Joaquim Escola – Realizou a sua formação Académica na Universidade de Coimbra onde, em 1987 obteve a licenciatura em Filosofia. Em 1990 obteve o diploma de Filosofia – Ramo de Formação Educacional. Em 1993 obteve o grau de Mestre em Filosofia Contemporânea. No ano de 2003 realizou o doutoramento em Educação na Universidade de Trás-os-Montes e Alto Douro. |
CD 05 - Discalculia e Baixo Rendimento a Matemática na Sociedade AtualLília Marcelino, CeiED – Universidade Lusófona Moderadora: Nadia Ferreira Terça-feira, 16 de julho, 14h00m - 15h00m Resumo Vivemos num mundo matematizado, onde a baixa numeracia pode ter sérias consequências educacionais e profissionais. A numeracia é a capacidade de compreender, usar e interpretar números em diversas situações, envolvendo habilidades como contagem, cálculo, interpretação de gráficos, resolução de problemas matemáticos e compreensão de conceitos numéricos. Ter uma boa numeracia é fundamental para lidar com questões financeiras, tomar decisões informadas e ter sucesso em várias áreas da vida. Esta comunicação tem como objetivo sensibilizar os professores de matemática para a importância da sua profissão na sociedade atual. Enfatiza práticas educativas orientadas para a natureza cumulativa da matemática como uma condição prévia para o sucesso educativo. Além disso, destaca a importância da identificação e recuperação atempada de competências numéricas desde os primeiros sinais de dificuldades, em alunos com discalculia ou com baixo rendimento em matemática. Nota biográfica
Lília Marcelino – Doutorada em Educação e Licenciada em Psicologia pela Universidade Lusófona. Investigadora integrada/colaboradora no CICANT/CeiED - Universidade Lusófona em Aprendizagem da Matemática. Membro efetivo da OPP e membro regular da Mathematical Cognition and Learning Society. É docente universitária na FCSEA – Universidade Lusófona e diretora do Núcleo da Discalculia – Apoio Psicopedagógico e Formação onde dá apoio a crianças e jovens com dificuldades na aprendizagem da matemática e formação acreditada a professores e psicólogos. |
CD 06 - Tópicos de Matemática e Arte – uma experiência pedagógicaPedro Freitas, Faculdade de Ciências da Universidade de Lisboa Moderador: João Almiro Terça-feira, 16 de julho, 10h00m - 11h00m Resumo Desde o ano letivo de 2018/19 que a Faculdade de Ciências da Universidade de Lisboa oferece uma disciplina sobre Matemática e Arte, inicialmente com 2 horas semanais e presentemente com 4 horas semanais, incluindo uma secção expositiva e uma secção prática, de discussão de artigos ou realização de exercícios. A disciplina é oferecida aos alunos de Ciências, bem como aos do Instituto Superior Técnico e aos do Mestrado em Ensino da Matemática. Nesta palestra, faremos uma descrição breve do funcionamento desta disciplina, apresentando um resumo dos seus conteúdos e discutindo um pouco a sua prática pedagógica, tanto a parte letiva como a das atividades práticas realizadas pelos alunos. Referiremos também alguns dos temas dos trabalhos finais, alguns dos quais vieram enriquecer o próprio currículo. Nota biográfica
Pedro Freitas – Doutorado em matemática, é Professor Auxiliar do Departamento de História e Filosofia das Ciências da Faculdade de Ciências da Universidade de Lisboa e membro do Centro Interuniversitário de História das Ciências e da Tecnologia. Para além do trabalho de ensino e investigação, ligado principalmente à matemática e à sua história, dedica-se também a assuntos de divulgação e de interação entre matemática e arte — em particular, colabora há alguns anos no estudo da obra geométrica de Almada Negreiros. |
CD 07 - Novas Aprendizagens Essenciais de Matemática B: A experiência numa turma-pilotoPedro Liberto Ferreira | Sandra Afonso Moderadora: Filipa Machado Terça-feira, 16 de julho, 11h30m - 12h30m Resumo Esta conferência oferece uma visão aprofundada sobre a implementação das novas aprendizagens essenciais de Matemática B, através das perspetivas de um diretor e de uma professora envolvidos numa turma-piloto. Este projeto inovador visa modernizar o currículo de Matemática B, alinhando-o com as exigências contemporâneas de ensino e aprendizagem. No seguimento da apresentação dos dados, destacaremos alguns exemplos práticos de tarefas implementadas em sala de aula. Estas tarefas foram desenhadas para promover uma aprendizagem ativa e participada, utilizando abordagens como a resolução colaborativa de problemas, trabalhos de projeto e o uso de tecnologias digitais. Concluiremos a conferência com um balanço do trabalho realizado até ao momento, abordando os desafios enfrentados e as estratégias adotadas para superá-los. Entre os desafios, destacam-se a criação de materiais didáticos, a formação contínua dos professores. Notas biográficas
Pedro Liberto Ferreira – Licenciado em Educação Física e Desporto pela Faculdade de Motricidade Humana – UTL, com Formação Especializada em Administração e Organização Escolar pelo IESF. Diretor da Escola Secundária José Saramago – Mafra desde maio de 2022, e professor nesta escola desde o ano letivo 1993-1994.
Sandra Afonso – Licenciada em Ensino da Matemática pela Faculdade de Ciências da Universidade de Lisboa. Concluiu o primeiro ano do Mestrado em Ensino da Matemática, na FCUL. É professora na Escola Secundária José Saramago – Mafra desde o ano letivo de 1996-1997. |
CD 08 - Os caminhos e desafios da avaliação externa digital: condição necessária ou suficiente?Luís Pereira dos Santos, Instituto de Avaliação Educativa, I.P. Moderador: Joaquim Pinto Segunda-feira, 15 de julho, 16h00m - 17h00m Resumo A avaliação das aprendizagens é um processo pedagógico incontornável nos projetos de ensino e de aprendizagem, sendo o elo que interliga o ato de ensinar com o ato de aprender. É através da avaliação que o sujeito ensinante percebe se o sujeito aprendente realmente aprendeu e a qualidade dessa aprendizagem. Para isso, a utilização dos resultados da avaliação das aprendizagens mostra-se imprescindível para a própria existência do ato educativo, para uma melhor adequação das didáticas e dos processos de aprendizagem, para uma partilha da responsabilidade do ato educativo.
Luís Pereira dos Santos – É Licenciado em Ensino da Física e Mestre em Didática das Ciências, pela Faculdade de Ciências da Universidade de Lisboa. Foi professor de Física e Química, vogal do Conselho Diretivo e Vice-Presidente do Conselho Executivo da Escola Secundária da Cidade Universitária, até 2001. Foi técnico da assessoria técnico-pedagógica do Júri Nacional de Exames, de 2001 a 2005. Foi Chefe de Divisão de Formação de Professores e Diretor de Serviços de Recursos Multimédia na DGIDC, entre 2005 e 2011. Foi Presidente do Júri Nacional de Exames de 2011 a fevereiro de 2019. Exerce atualmente o cargo de Presidente do Conselho Diretivo do IAVE. |
CD 09 - A matemática nos estudos internacionais da OCDE: PISA, PISA-VET e PIAACAnabela Serrão, Instituto de Avaliação Educativa, I.P. Moderador: Joaquim Pinto Quarta-feira, 17 de julho, 10h00m - 11h00m Resumo A OCDE coordena vários estudos de avaliação de competências: o PISA para os alunos de 15 anos, o PISA-VET para os formandos de programas iniciais de educação e formação profissional e o PIAAC para os jovens e adultos entre os 16 e os 65 anos. Em todos eles, os conhecimentos e as competências matemáticas integram os quadros de referência de avaliação, atribuindo a este domínio uma grande importância. Nesta comunicação serão apresentadas e discutidas as diferentes abordagens da OCDE utilizadas na avaliação deste domínio. Nota biográfica
Anabela Serrão – Membro do Conselho Diretivo do Instituto de Avaliação Educativa, I.P. desde 2019. Atualmente é coordenadora nacional dos vários estudos internacionais que o IAVE implementa em Portugal, entre eles o PISA da OCDE. Integra os grupos de trabalho de desenvolvimento dos questionários de contexto do TIMSS e PIRLS. É membro do PISA Analysis and Dissemination Group da OCDE. É licenciada em Sociologia pela FCSH-UNL com uma especialização em Análise de Dados para as Ciências Sociais pelo ISCTE-IUL. Possui ainda várias formações nas áreas da análise de dados e da estatística. |
CD 10 - Matemática Computacional: um convite à MatemáticaCarlos Albuquerque, Faculdade de Ciências, Universidade de Lisboa Moderador: Paulo Correia Terça-feira, 16 de julho, 10h00m - 11h00m Resumo Nesta conferência vamos explorar alguns aspetos da Matemática Computacional e ver como são uma fonte de desafios e conexões em múltiplas áreas da Matemática, desde as mais abstratas até às aplicações na vida quotidiana e na tecnologia. Como ponto de partida teremos os números, os polinómios e dois métodos que fazem parte das Aprendizagens Essenciais de Matemática do 12.º ano: o método da bisseção e o método de Newton-Raphson. A combinação de Python e Matemática será o veículo para os aspetos mais práticos e visuais destas explorações. Um dos objetivos desta conferência é suscitar ideias para trabalhos de projeto com os alunos de Matemática. Nota biográfica
Carlos Albuquerque – É Professor Auxiliar do Departamento de Matemática da Faculdade de Ciências da Universidade de Lisboa. Tem desenvolvido investigação em projetos interdisciplinares e tem participado na formação inicial de professores de Matemática em diversas funções. Foi membro do Grupo de Trabalho de Matemática que elaborou as "Recomendações para a melhoria das aprendizagens dos alunos em Matemática" (2020) e é co-autor das novas Aprendizagens Essenciais de Matemática para o Ensino Secundário. |
CD 11 - Percursos que contam em QuarteiraNélida Filipe, Agrupamento de escolas Dra. Laura Ayres Moderador: Helder Martins Terça-feira, 16 de julho, 11h30m - 12h30m Resumo Os Percursos Que Contam são uma co-criação do Núcleo do Algarve da APM e do Centro de Ciência Viva do Algarve. Professores e alunos do ensino secundário do agrupamento de escolas Dra. Laura Ayres, no âmbito da disciplina de Cidadania e Desenvolvimento e Matemática, criaram os “Percursos que Contam-Quarteira Antiga”. Estiveram envolvidos 14 professores de várias áreas disciplinares e oito turmas do ensino secundário. Num trabalho de articulação, colaboração e muito entusiasmo, foi possível criar um percurso pela cidade de Quarteira que simultaneamente apela ao convívio entre amigos e família, à descoberta da história, aspetos culturais e curiosidades da cidade e ainda, à resolução de desafios matemáticos alusivos aos vários pontos de interesse. O livro “Percursos que contam- Quarteira antiga” e que faz parte da coleção Famílias Exploradoras, foi lançado oficialmente no dia 14 de março de 2024 e contou com o apoio da Junta de freguesia de Quarteira e CML. Nota biográfica
Nélida Filipe – Licenciada em Ensino da Matemática, pela FCUC, mestre em Educação Matemática, pela UE e doutora em Educação-Didática da Matemática Instituto de Educação da UL. É professora no Agrupamento de Escolas Dra. Laura Ayres e professora adjunta convidada na ESEC da UALG. É coautora das novas Aprendizagens Essenciais de Matemática para o Ensino Secundário e Profissional, sendo igualmente coautora de manuais escolares. É Membro da equipa do núcleo do Algarve-APM. |
CD 12 - Ensino Profissional e as Novas Aprendizagens do Ensino da MatemáticaCristina Fernandes, Agrupamento de Escolas de Sampaio Moderador: José Miguel Sousa Terça-feira, 16 de julho, 11h30m - 12h30m Resumo As Aprendizagens Essenciais de Matemática para os Cursos Profissionais (AEMCP) serão aplicadas no ano letivo de 2024/2025, sendo que a sua operacionalização antecipada ocorreu no ano letivo 2023/2024 em oito turmas piloto e na qual participaram as autoras desta comunicação. Neste sentido, propõe-se a partilha de uma visão geral das AEMCP e orientações metodológicas, tentando sinalizar as principais mudanças em causa no novo quadro curricular. As autoras contribuirão ainda com uma síntese dos principais desafios que se poderão colocar, procurando suscitar uma reflexão conjunta, a partir da aplicação de algumas tarefas e experiências de ensino, que seja mobilizadora do subsequente processo de generalização das AEMCP. Notas biográficas
Cristina Maria Bata Fernandes – É licenciada em Ensino da Matemática pela Faculdade de Ciências da Universidade de Lisboa e concluiu o primeiro ano do mestrado em Educação, na área de especialização em Formação e Aprendizagem ao Longo da Vida, na FCUL. É docente do Agrupamento de Escolas de Sampaio e é professora de uma turma piloto das AE para os Cursos Profissionais.
Elsa Maria Cardoso Gomes – É licenciada em Matemática, Ramo Educacional pela Faculdade de Ciências da Universidade do Porto (FCUP) e concluiu o 1º ano do Mestrado em Deteção Remota, na FCUP. É docente da Escola Secundária de Paços de Ferreira. É professora de uma turma piloto das AE para os Cursos Profissionais.
Marília André do Rosário – É licenciada em Matemática pela Faculdade de Ciências da Universidade do Porto e Mestre em Supervisão Pedagógica em Ensino da Matemática pela Universidade do Minho. É docente do Agrupamento de Escolas Tomaz Pelayo. Foi Professora Acompanhante do Plano de Ação para a Matemática, Supervisora no Processo de classificação de Provas do IAVE, orientadora de estágio da FCUP e UM, formadora acreditada pelo CCPFC e é professora de uma turma piloto das AE para os Cursos Profissionais. |
CD 13 - Promover práticas de pensamento computacional no ensino da matemática nos 1.º e 2.º Ciclos do Ensino BásicoRui Gonçalo Espadeiro, Agrupamento de Escolas de Redondo Moderador: António Cardoso Segunda-feira, 15 de julho, 16h00m - 17h00m Resumo Nesta conferência pretendemos apresentar e discutir práticas de Pensamento Computacional (PC) associadas a algumas das tarefas desenvolvidas na formação realizada pela Associação de Professores de Matemática (APM) no âmbito do Projeto-Piloto MatemaTIC, que estão presentes no e-book “Contributos para o desenvolvimento do pensamento computacional em Matemática: Materiais de apoio para os professores do 1.º ciclo do ensino básico”. O projeto resultou de uma parceria entre DGE e a APM com o objetivo de promover a articulação entre as Aprendizagens Essenciais de Matemática e as Orientações Curriculares para as TIC no 1.º ciclo do ensino básico e a capacitação de professores de 1.º ciclo para a integração do PC em tarefas de Matemática para este ciclo de ensino. Na conferência serão apresentadas as tarefas, propostas para a sua exploração bem como resoluções realizadas por professores em contexto de formação e alunos em sala de aula. Notas biográficas
Rui Gonçalo Espadeiro – Professor de Matemática do ensino básico e secundário. Licenciado em Ensino de Matemática pela Universidade de Évora e mestre em Ciências da Educação, variante de Supervisão Pedagógica, na mesma universidade. Integrou as equipas que redigiram as Aprendizagens Essenciais da Matemática para o Ensino Básico e Secundário. Integra também o Grupo de Trabalho de Desenvolvimento Curricular e Profissional de Matemática.
Renata Carvalho – Licenciada em Ensino na variante de Matemática e Ciências da Natureza pela ESE de Portalegre. Possui Mestrado em Educação na área de Didática da Matemática pela Faculdade de Ciências da Universidade de Lisboa e Doutoramento em Educação, na mesma área, pelo Instituto de Educação da Universidade de Lisboa. Tem colaborado em projetos e encontros nacionais e internacionais na área da Educação Matemática e na formação contínua de professores. Colabora, desde 2016/17 com a ESE de Lisboa na formação inicial de professores. Atualmente é Diretora do Centro de Formação da APM.
Neusa Branco – Professora Adjunta na Escola Superior de Educação, Instituto Politécnico de Santarém. Licenciada em Ensino da Matemática, mestre em Educação-Didática da Matemática e doutorada na mesma área pelo Instituto de Educação da ULisboa. É coordenadora do Mestrado em Ensino do 1.º CEB e de Matemática e Ciência Naturais no 2.º CEB. Tem trabalhado em temas como: Ensino-aprendizagem da Álgebra, Didática da Matemática, Educação STEAM; Conexões matemáticas e Pensamento computacional. |
CD 14 - Pensamento estatístico: a importância decisiva do contextoSusana Carreira, Universidade do Algarve Moderadora: Nadia Ferreira Quarta-feira, 17 de julho, 10h00m - 11h00m Resumo A Estatística utiliza formas de pensamento específicas e o desenvolvimento do pensamento estatístico no ensino secundário deve incluir abordagens exploratórias de dados autênticos, em que se detetam padrões e tendências, se identificam modelos e se reconhecem casos excecionais num conjunto de dados. Os contextos devem ser parte integrante da análise e interpretação de dados reais, de tal modo que os alunos consigam compreender e discutir criticamente o mundo em seu redor e a realidade económica, social e cultural em que participam. Trata-se, portanto, de promover e desenvolver o sentido crítico dos alunos, enquanto cidadãos produtores e consumidores de dados. A educação estatística inclui a tomada de consciência de que inúmeros problemas da atualidade são abordados a partir da obtenção e análise de grandes quantidades de dados. Em sintonia com as novas Aprendizagens Essenciais de Matemática A, Matemática B e Matemática dos Cursos Profissionais, do ensino secundário, darei especial atenção à importância do contexto de um problema ou de uma investigação estatística para o desenvolvimento do pensamento estatístico. Nota biográfica
Susana Carreira – Professora Associada da Faculdade de Ciências e Tecnologia da Universidade do Algarve e Professora Associada Convidada do Instituto de Educação da Universidade de Lisboa. É doutorada em Didática da Matemática pela Universidade de Lisboa. Desenvolve investigação em Educação Matemática, nomeadamente nas seguintes áreas: modelação e aplicações no ensino e aprendizagem da matemática; tecnologias na educação matemática, resolução de problemas, criatividade matemática, aspetos afetivos na educação matemática. É autora de livros e artigos científicos em revistas nacionais e internacionais. Tem orientado estudantes de mestrado e de doutoramento, em Portugal e no Brasil. Fez parte da equipa que elaborou as novas Aprendizagens Essenciais de Matemática para o ensino secundário, homologadas em 2023. |
CD 15 - Modelos matemáticos em finanças nas novas Aprendizagens Essenciais de MatemáticaHelder Martins, Escola Secundária António Damásio, Lisboa Moderador: João Terroso Terça-feira, 16 de julho, 9h00m - 10h00m Resumo Nesta conferência, pretendemos analisar os modelos matemáticos em finanças à luz das novas AE de Matemática para o Ensino Secundário regular (Mat A, Mat B e MACS).e Profissional, homologadas em janeiro de 2023, discutindo o seu papel e quais as dimensões que são relevantes. Será efetuada uma análise do que foi feito nas turmas piloto tendo por base as coletâneas já publicadas. Notas biográficas
Helder Manuel Martins – Licenciado em Ensino da Matemática, pela FCUL; é mestre em Educação, especialidade de STEM; pela FCT NOVA; e é Doutorando em Educação, Inovação Educativa, pela FCT/FCSH/ISPA. É orientador de estágios a formandos do curso de Mestrado em Ensino de Matemática no 3.º ciclo do Ensino Básico e no Secundário da FCT NOVA. Colaborou nos projetos T3 – Teaching Teachers with Technology, da APM, e REANIMAT, da FCUL e da FCG. É coautor de manuais escolares de Matemática para o Ensino Secundário; é coautor do relatório “Recomendações para a melhoria das aprendizagens dos alunos em Matemática”; e, coautor das novas AE para a Matemática do Ensino Secundário.
Nélida Filipe – Licenciada em Matemática, pela FCTUC; é mestre em Educação Matemática; pela UE; e é Doutora em Educação-Didática da Matemática pelo IE-UL. É professora na Escola Secundária Dra. Laura Ayres em Quarteira e Professora Adjunta Convidada na ESEC da UALG. É professora supervisora de alunas do curso de Mestrado em EB do 1.ºciclo e Ensino de MC no 2.º ciclo do EB na ESEC da UALG. Colaborou num projeto de FCT sobre literacia Estatística, é membro da equipa do Núcleo da APM no Algarve. É coautora de manuais escolares de Matemática para o Ensino Profissional; é coautora e formadora das novas AE para a Matemática do Ensino Secundário. |
CD 16 - Os manuais e as novas Aprendizagens Essenciais de Matemática no Ensino ProfissionalMaria Augusta Ferreira Neves | Bruno Roque | Pedro Rocha Almeida Moderador: Manuel Lourenço Terça-feira, 16 de julho, 14h00m - 15h00m Resumo Os manuais desempenham um papel fulcral no processo ensino e aprendizagem, proporcionando uma base sólida para os alunos e professores. Com as Novas Aprendizagens Essenciais de Matemática para o Ensino Profissional, vários foram os desafios colocados na elaboração dos manuais, tais como proporcionar experiências de aprendizagem inovadoras, enriquecedoras, promotoras de uma abordagem mais prática e contextualizada da Matemática e contribuir para que os alunos se tornem cidadãos mais capazes de tomar decisões, reflexivos empenhados e participativos. Nesta conferência evidenciaremos aspetos relevantes da estrutura dos manuais e a forma como os torna adequados a todos alunos, na metodologia e na avaliação constante e diversificada nas suas várias dimensões. Notas biográficas
Maria Augusta Ferreira Neves – A sua vasta experiência como docente do Ensino Básico, Secundário e Superior, assim como a sua formação académica – Licenciada, Mestre e Doutorada Está em contacto permanente com professores e escolas de todo o país, em particular, através de ações de formação. Esta proximidade com a diversidade de escolas, professores e alunos permite-lhe conhecer com pormenor as diferentes realidades e necessidades de cada um. Nos últimos anos, participou em trabalhos de investigação relacionados com a diversificação de metodologias e modelos de avaliação, para promover o sucesso.
Bruno Roque – Licenciado e mestre pela Faculdade de Ciências da Universidade do Porto nas áreas de Matemática Educacional e Engenharia Matemática. Professor de Matemática do 3.º ciclo e do Ensino Secundário, desde 2002. Lecionou disciplinas de Matemática e Estatística no Ensino Superior. Nas escolas por onde passou, desempenhou funções de gestão intermédia, nomeadamente na coordenação do “Plano de Ação para a Matemática”, como elemento da equipa de avaliação interna e do Agrupamento de Exames do Tâmega. Formador de professores nas áreas da Matemática, Tecnologia Educativa e Educação Matemática.
Pedro Rocha Almeida – Professor de Matemática do 3.º ciclo e do Ensino Secundário, desde 2002. Licenciado em Ensino de Matemática pela Universidade de Aveiro, mantém com esta instituição uma estreita colaboração. Integrou a equipa de autores do programa e dos manuais da disciplina de Economia e Métodos Quantitativos, no âmbito do projeto "Falar Português - Reestruturação curricular do Ensino secundário de Timor-Leste”. Atualmente, colabora no projeto “Aveiro Education and Social Alliance”, no Departamento de Matemática. |
CD 17 - A aprendizagem da Matemática em atividades STEAM nos 1.º e 2.º ciclos do ensino básicoNeusa Branco, ESE de Santarém | Polo de Literacia Digital e Inclusão Social, CIAC, UAlg Moderador: Ricardo Vicente Terça-feira, 16 de julho, 9h00m - 10h00m Resumo Nesta conferência pretendemos apresentar e discutir algumas propostas de trabalho enquadradas na abordagem STEAM, explicitando as áreas envolvidas, nomeadamente as conexões entre a matemática e as ciências, a sua concretização e exemplos de aprendizagens que podem promover. Estas propostas visam envolver os alunos em atividades matemáticas significativas que promovam o desenvolvimento do seu conhecimento e da capacidade de o aplicar em contextos não matemáticos. A abordagem STEAM seguida procura também contribuir para a promoção de atitudes positivas face à Matemática e o reconhecimento da importância do seu conhecimento para a resolução de problemas de diferentes áreas. Na conferência serão apresentados exemplos do trabalho nestas propostas, em particular envolvendo a utilização de objetos robóticos simples ou contextos de programação, a partir de problemas ou desafios colocados aos alunos. Notas biográficas
Neusa Branco – Professora Adjunta na Escola Superior de Educação, Instituto Politécnico de Santarém. Licenciada em Ensino da Matemática, mestre em Educação-Didática da Matemática e doutorada na mesma área pelo Instituto de Educação da ULisboa. É coordenadora do Mestrado em Ensino do 1.º CEB e de Matemática e Ciência Naturais no 2.º CEB. Tem trabalhado em temas como: Ensino-aprendizagem da Álgebra, Didática da Matemática, Educação STEAM; Conexões matemáticas e Pensamento computacional. Bento Cavadas – Professor Adjunto na Escola Superior de Educação, Instituto Politécnico de Santarém. Licenciado em Ensino de Biologia e Geologia e doutor em Política e Fundamentos Educativos pela Universidade de Salamanca. É subcoordenador do Mestrado em Ensino do 1.º CEB e de Matemática e Ciência Naturais no 2.º CEB. Autor de manuais escolares de Ciências Naturais. Os seus interesses de investigação são nas áreas da didática das ciências, formação de professores, manuais escolares e integração das ciências e da matemática. Integra a equipa do CreativeLab_Sci&Math®. |
CD 18 - Dados nos primeiros anos…quais as novidades?!Ana Caseiro, Escola Superior de Educação de Lisboa Moderadora: Nadia Ferreira Terça-feira, 16 de julho, 10h00m - 11h00m Resumo Embora o tema Organização e tratamento de dados surgisse em anteriores documentos curriculares, nas Aprendizagens Essenciais (AE) atualmente em vigor, o tema Dados e Probabilidades surge com maior destaque, tendo como principal objetivo o desenvolvimento da literacia estatística dos alunos do 1.º ciclo. No documento são apresentadas, de forma clara e direta, sugestões de trabalho a serem desenvolvidas com os alunos, sendo frisada a importância de lhes possibilitar experienciarem dois tipos distintos de trabalho: (i) realização de investigações estatísticas; e (ii) análise de representações gráficas reais. Dessa forma, esta conferência tem como principal objetivo discutir estes dois modos de trabalho, focando em exemplos práticos realizados com alunos do 1.º ciclo, e tentando discutir as potencialidades e dificuldades da realização deste tipo de trabalho, quer pelos alunos quer pelos professores. Nota biográfica
Ana Caseiro – Doutorada em Educação, ramo de Didática da Matemática, pelo Instituto de Educação da UL. Professora adjunta da Escola Superior de Educação de Lisboa onde coordena, entre outros, o domínio científico da Matemática e a Licenciatura em Educação Básica. Coordena e participa em projetos de investigação na área da Educação Matemática, com enfoque nos primeiros anos, e com especial destaque para a área da Análise de Dados. Colabora com a APM, sendo membro da equipa de coordenação do GTI. |
ProfMat 2024 - Sessões Práticas (2h)
As sessões práticas são propostas e dinamizadas por participantes no encontro, sobre temas, abordagens e materiais didáticos, em que é prevista a realização de trabalho prático e discussão, com um momento final para debate coletivo. Para além dos Grupos de trabalho e dos Parceiros da APM, qualquer participante pode submeter uma proposta de Sessão Prática (no separador "Profmat 2024"). A lista completa de sessões práticas é divulgada a partir do dia 5 de junho.
|
SP 01 |
Estratégias promotoras de pensamento crítico no ensino/aprendizagem da matemática (Resumo) Caroline Dominguez | Eva Morais | Sandra Ricardo Público: GERAL |
Terça-feira, 16 de julho 14h00 - 16h00 |
ESRBP Bloco 2, Piso 2, Sala 20 |
| SP 02 |
Primeiros passos com a calculadora gráfica Casio fx-CG50 (Resumo) Ana Margarida Dias, Casio School Coordinator Público: SECUNDÁRIO |
Terça-feira, 16 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 20 |
| SP 03 |
Modelos Matemáticos para a Cidadania com a calculadora gráfica Casio fx-CG50 (Resumo) Dolcínia Almeida, Agrupamento de Escolas de Águeda Sul Público: SECUNDÁRIO |
Terça-feira, 16 de julho 14h00 - 16h00 |
ESRBP Bloco 2, Piso 2, Sala 19 |
| SP 04 |
Desvendando a Matemática com Micro:bit e TI-Nspire: Uma Abordagem Gamificada (Resumo) Alexandra Rodrigues, Leiria International School Público: 3.º CICLO e SECUNDÁRIO |
Terça-feira, 16 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 1, Sala 16 |
| SP 05 |
A dinâmica e a interatividade entre aplicações da tecnologia TI-Nspire - vantagens na aprendizagem de Matemática no ensino secundário (Resumo) Eduardo Cunha, Agrupamento de Escolas António Correia de Oliveira Público: SECUNDÁRIO |
Terça-feira, 16 de julho 14h00 - 16h00 |
ESRBP Bloco 2, Piso 2, Sala 18 |
| SP 06 |
Da Teoria à Prática: Workshop MILAGE para Co-criação Educacional (Resumo) Mauro Figueiredo, Universidade do Algarve Público: GERAL |
Quarta-feira, 17 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 20 |
| SP 07 |
Matemática fora da sala de aula: criar trilhos com o Math City Map (Resumo) Manuel João Marques, APM Público: GERAL |
Quarta-feira, 17 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 1, Sala 15 |
| SP 08 |
A Importância dos projetos STEM nas Novas Aprendizagens de Matemática com a TI-Nspire CX II-T (Resumo) António Vidal, Agrupamento de Escolas Júlio Dantas, Lagos Público: 2.º CICLO, 3.º CICLO e SECUNDÁRIO |
Quarta-feira, 17 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 19 |
| SP 09 |
Apresentações informais de conceitos e resultados matemáticos (Resumo) Atractor, Associação Atractor – matemática interactiva Público: SECUNDÁRIO |
Terça-feira, 16 de julho 14h00 - 16h00 |
ESRBP Bloco 2, Piso 2, Sala 17 |
| SP 10 |
Geometria Sintética com o GeoGebra (Resumo) José Carlos Pereira Público: SECUNDÁRIO |
Terça-feira, 16 de julho 14h00 - 16h00 |
ESRBP Bloco 2, Piso 1, Sala 16 |
| SP 11 |
As pontes entre a Matemática e a sua História nas Aprendizagens Essenciais da Matemática (Resumo) Teresa Costa Clain, GHMEM do CIDMA/Universidade de Aveiro Público: 3.º CICLO e SECUNDÁRIO |
Quarta-feira, 17 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 18 |
| SP 12 |
Corrida de Carros – usando Python e funções polinomiais e trigonométricas (Resumo) Sandra Gaspar Martins, Instituto Superior de Engenharia de Lisboa Público: SECUNDÁRIO |
Terça-feira, 16 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 19 |
| SP 13 |
Resolução de problemas e pensamento computacional (Resumo) Célia Mestre, Escola Superior de Educação, Instituto Politécnico de Setúbal Público: 1.º CICLO e 2.º CICLO |
Terça-feira, 16 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 18 |
| SP 14 |
Atribuir significado à divisão: um itinerário para a sala de aula dos naturais às frações (Resumo) Miguel Ribeiro, Universidade Estadual de Campinas (UNICAMP), Brasil Público: 1.º CICLO e 2.º CICLO |
Quarta-feira, 17 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 17 |
| SP 15 |
Descobrir volumes em embalagens e outras que tais (Resumo) Isabel Costa Belo, Agrupamento de Escolas Martim de Freitas, Coimbra Público: 2.º CICLO |
Terça-feira, 16 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 17 |
| SP 16 |
A aprendizagem de Geometria com o GeoGebra (Resumo) Mariana Ribeiro | António Domingos | Helder Martins Público: SECUNDÁRIO |
Quarta-feira, 17 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 1, Sala 16 |
| SP 17 |
Tarefas de Modelação – O foco nas ações do professor (Resumo) António Júlio Aroeira, Escola Básica e Secundária da Madalena Público: SECUNDÁRIO |
Terça-feira, 16 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 16 |
| SP 18 |
Estatística - Análise De Dados E Representações Gráficas Com O Geogebra (Resumo) Maria José Teixeira Do Nascimento, Escola Secundária São Pedro Público: 2.º CICLO, 3.º CICLO e SECUNDÁRIO |
Terça-feira, 16 de julho 14h00 - 16h00 |
ESRBP Bloco 2, Piso 2, Sala 16 |
| SP 19 |
O Software Intuitivo – Avaliações em Formato Digital (Resumo) Filipa Susana da Graça Ferreira, Agrupamento de Escolas José Afonso, Alhos Vedros Público: GERAL |
Terça-feira, 16 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 15 |
| SP 20 |
Eu e o mundo, a maldita matemática e outras histórias – uma abordagem interdisciplinar entre a literatura infantojuvenil e a matemática (Resumo) Susana Colaço | Maria Clara Martins Público: 1.º CICLO e 2.º CICLO |
Terça-feira, 16 de julho 14h00 - 16h00 |
ESRBP Bloco 2, Piso 2, Sala 15 |
| SP 21 |
Explorando a Geometria com o Scratch: Uma abordagem prática para professores de Matemática (Resumo) Nuno Raínho | Carlos Leão Público: 2.º CICLO e 3.º CICLO |
Quarta-feira, 17 de julho 9h00 - 11h00 |
ESRBP Bloco 2, Piso 2, Sala 16 |
RESUMOS
SP 01 - Estratégias promotoras de pensamento crítico no ensino/aprendizagem da matemáticaCaroline Dominguez | Eva Morais | Sandra Ricardo Terça-feira, 16 de julho, 14h00m - 16h00m Resumo As Aprendizagens Essenciais de Matemática apontam o pensamento crítico como uma das competências transversais a desenvolver no ensino e na aprendizagem, sendo que esta competência assume um papel fundamental no contexto atual em que vivemos, de mudanças e desafios constantes. Esta sessão prática tem como objetivos: refletir sobre a importância do pensamento crítico no ensino e na aprendizagem da Matemática; conhecer e aplicar taxonomias de pensamento crítico para a elaboração de objetivos de aprendizagem na Matemática com o intuito de promover, de forma progressiva, o desenvolvimento do pensamento crítico; selecionar e adaptar estratégias adequadas aos objetivos a atingir, e, em particular, refletir sobre o potencial de estratégias cooperativas. Nota biográficaCaroline Dominguez – Doutorada em Socio-Economia pela Universidade de Toulouse-Le-Mirail (França), Caroline Dominguez é docente no Departamento de Engenharia da UTAD. Publica sobre gestão industrial e sobre desenvolvimento do pensamento crítico (PC) no ensino superior. Coordena o grupo de PC da UTAD-WebPACT e a Rede Portuguesa de PC-Crithinknet e participa(ou) e/ou coordena(ou) projetos nacionais e internacionais nessa área. Ministra(ou) formação focada no desenvolvimento do PC para docentes e não docentes. Eva Morais – Licenciada em Matemática (Ensino) pela Universidade de Trás-os-Montes e Alto Douro (UTAD), mestre em Matemática Aplicada pela Universidade de Coimbra e doutorada em Matemática Aplicada à Economia e Gestão pela Universidade de Lisboa (ISEG). É docente no Departamento de Matemática na UTAD. Na sua investigação, interessa-se atualmente pela validação de instrumentos de avaliação de competências de pensamento crítico em estudantes de diferentes níveis de ensino. Sandra Ricardo – Licenciada em Matemática (Formação Educacional) pela Universidade Nova de Lisboa, mestre em Matemática pela Universidade de Coimbra e doutorada em Matemática pelo Institut National des Sciences Appliquées de Rouen (França). É docente no Departamento de Matemática da Universidade de Trás-os-Montes e Alto Douro e membro do Centro de Investigação e Intervenção Educativas da Universidade do Porto. Os seus atuais interesses de investigação incluem a formação de professores e a promoção de competências de pensamento crítico na educação. |
SP 02 - Primeiros passos com a calculadora gráfica Casio fx-CG50Ana Margarida Dias, Casio School Coordinator | Grupo Casio+ Terça-feira, 16 de julho, 9h00m - 10h00m Resumo Uma das ideias chave das Aprendizagens Essenciais para o ensino secundário, homologadas em janeiro de 2023 é o recurso sistemático à tecnologia, em particular, a utilização das calculadoras gráficas. A integração da tecnologia é considerada como indispensável na abordagem exploratória de ideias e conceitos matemáticos, pelas possibilidades que oferece aos alunos de experimentarem, visualizarem, representarem e simularem. Nesta sessão vamos conhecer um pouco do modo de funcionamento da calculadora gráfica Casio fx-CG50. A resolução de tarefas será o ponto de partida para explorar quatro dos menus desta calculadora, o Menu run-matrix, o Menu Graph, o Menu Statistics e o Menu Equation. Os participantes terão oportunidade de trabalhar, em pequenos grupos, tarefas envolvendo gráficos, listas e regressões. Nota: Poderá ser emprestada uma calculadora Casio fx-CG50 aos formandos que não possuem este equipamento. Nota biográficaAna Margarida Dias – Licenciada em Matemática Aplicada. Certificada como formadora na área e domínio das Didáticas Específicas da Matemática e Tecnologia Educativas na Sala de Aula desde 2005. Coordenadora Pedagógica na Casio Portugal. Integra o Grupo de Trabalho Casio+ da APM desde o seu inicio. |
SP 03 - Modelos Matemáticos para a Cidadania com a calculadora gráfica Casio fx-CG50Dolcínia Almeida, Agrupamento de Escolas de Águeda Sul | Grupo Casio+ Terça-feira, 16 de julho, 14h00m - 16h00m Resumo Nas aprendizagens essenciais da Matemática no ensino secundário surge como ideia inovadora do currículo a “Matemática para a cidadania” que pretende fazer parte integrante da formação geral dos jovens. Assim, nesta sessão prática pretende-se explorar alguns modelos matemáticos de processos eleitorais e de modelos financeiros usando as potencialidades da tecnologia na resolução de problemas. No que se refere a ideias chave das aprendizagens essenciais destaca-se o “Recurso sistemático à tecnologia” uma vez que as tarefas previstas se proporcionam a incentivar a exploração de ideias e conceitos, integrando a tecnologia como alavanca para a compreensão e resolução de problemas. Nesta sessão vai ser abordada a programação em Python, apresentada de forma a conhecerem as funcionalidades básicas com atividades relevantes para o desenvolvimento de processos algorítmicos, de um pensamento estruturado e do raciocínio lógico, a resolução de problemas, além de promover o desenvolvimento do pensamento computacional. Nota: Poderá ser emprestada uma calculadora Casio fx-CG50 aos formandos que não possuem este equipamento. Nota biográfica Dolcínia Almeida – Licenciada e Mestre em Ensino da Matemática. Certificada como formadora na área e domínio das Didáticas Específicas da Matemática desde 2000. Professora Acompanhante Local do Programa Ajustado de Matemática no ensino secundário, em 1999, e Professora Acompanhante do Plano de Ação para a Matemática no ensino básico. Desde 2012, integra o Grupo de Trabalho Casio+ da APM. |
SP 04 - Desvendando a Matemática com Micro:bit e TI-Nspire: Uma Abordagem GamificadaAlexandra Rodrigues, Leiria International School | Grupo T3 Portugal Terça-feira, 16 de julho, 9h00m - 11h00m Resumo O objetivo da sessão é explorar recursos, ideias estimulantes, desafios e experiências que destacam as oportunidades proporcionadas pelo Micro:bit™ e tecnologia TI Nspire Cx II-T. Os participantes poderão integrar o Micro:bit em tarefas para que os alunos aprendam a programar ou integrá-lo em atividades gamificadas. Assente numa estratégia de gamificação, pretende-se promover a motivação, facilitar a inclusão e diversidade em sala de aula, enquanto se desenvolve o pensamento computacional, programando em Python. Através de atividades práticas e interativas, que demonstram algumas das potencialidades destas tecnologias no desenvolvimento das competências previstas nas Aprendizagens Essenciais, vamos descobrir maneiras criativas de introduzir elementos lúdicos no ensino da Matemática, tornando a aprendizagem uma experiência empolgante e memorável para os alunos. Notas biográficas Alexandra Rodrigues – Membro do Grupo de Trabalho T3 da APM, doutoranda em Didática na Universidade de Trás-os-Montes e Professora de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário no Leiria International School. Joana Duarte – Professora do 2.º e 3.º Ciclos do Ensino Básico e do Ensino secundário no grupo 550, Licenciada em Matemática pela Universidade Católica Portuguesa e Pós-Graduada em Gestão Financeira e Fiscal de Empresas pela Faculdade de Economia da Universidade de Coimbra. Certificada pelo CCPFC, é Formadora do Grupo de Trabalho T3 da APM e recentemente, Professora na Escola Superior de Educação de Viseu. |
SP 05 - A dinâmica e a interatividade entre aplicações da tecnologia TI-Nspire - vantagens na aprendizagem de Matemática no ensino secundárioEduardo Cunha, Agrupamento de Escolas António Correia de Oliveira | Grupo T3 Portugal Terça-feira, 16 de julho, 14h00m - 16h00m Resumo A tecnologia TI-Nspire, mais do que uma calculadora gráfica, cujo software de computador é muito mais do que um emulador, potencia a aprendizagem matemática com recurso a múltiplas representações e com interações dinâmicas entre si. As novas AEs das matemáticas para o Ensino Secundário reforçam a utilização de diversos suportes tecnológicos, como a folha de cálculo, os AGDs, as representações de funções e estatísticas, ou editor de Python. Com a TI-Nspire, todos estes suportes estão presentes “na palma da mão” e na mesma plataforma tecnológica, em aplicações de fácil utilização e com a possibilidade de se interligarem entre si de forma bastante natural. Vamos tratar exemplos, baseados no trabalho realizado com alunos de uma turma experimental das novas aprendizagens na Matemática A, de utilização da folha de cálculo e o tratamento estatístico, da representação gráfica de funções e transformações dos seus gráficos, e da integração do editor de Python com a aplicação de gráficos em torno da aprendizagem da função afim. Nota: Serão fornecidas calculadoras gráficas TI-Nspire CX II-T, mas poderão utilizar com vantagem o vosso computador portátil com o respetivo software instalado e atualizado. Notas biográficas Eduardo Cunha – Membro do GT T3 da APM, Mestre em Tecnologia Educativa, Coordenador do Projeto Academia das Ciências pelo Oceano – CCVnE e Professor do AE António Correia de Oliveira. Raul Gonçalves – Membro do GT T3 da APM, do GT do Desenvolvimento Curricular e Profissional em Matemática para o Ensino Secundário e professor de uma turma experimental de matemática A das novas AEs de matemática A no AE de Ermesinde. |
SP 06 - Da Teoria à Prática: Workshop MILAGE para Co-criação EducacionalMauro Figueiredo, Universidade do Algarve Quarta-feira, 17 de julho, 9h00m - 11h00m Resumo Nesta sessão prática, iremos explorar a criação de conteúdos educativos digitais na MILAGE. Pretende-se capacitar os professores para que possam transformar os alunos em co-criadores do conhecimento, incentivando-os a participar ativamente na criação de conteúdos educacionais e no desenvolvimento de suas próprias competências curriculares e transversais através da MILAGE. Ao habilitar os professores a integrar os alunos no processo de criação de conteúdos, esperamos fomentar um ambiente de aprendizagem mais colaborativo e inovador, onde os alunos não são apenas consumidores de informações, mas também contribuem ativamente para a construção do conhecimento. Esta abordagem não apenas aumenta a motivação dos alunos, mas também desenvolve suas competências críticas e criativas. Nota: Os participantes devem trazer um computador. Nota biográfica Mauro Figueiredo – Professor na Universidade do Algarve. Doutorado em Engenharia Informática pela Universidade de Salford, Reino Unido. Os seus interesses de investigação incidem na utilização das Tecnologias de Informação e Comunicação para a Educação, aprendizagem móvel, realidade virtual e aumentada. Desenvolveu a plataforma MILAGE APRENDER+ para a aprendizagem móvel. |
SP 07 - Matemática fora da sala de aula: criar trilhos com o Math City MapManuel João Marques, APM Quarta-feira, 17 de julho, 9h00m - 11h00m Resumo Será que a Matemática está em todo o lado? Para os alunos conseguirem ver a matemática que os rodeia, é necessário que o professor os ensine a ver. A criação de tarefas em contexto real, fora da sala de aula, promove a formulação e resolução de problemas, o estabelecimento de conexões matemáticas, o pensamento crítico, mas também o trabalho colaborativo e a criatividade, indo assim ao encontro das orientações das Aprendizagens Essenciais para o Ensino Básico e o Ensino Secundário. O recurso à tecnologia, e em particular à aplicação Math City Map (disponível gratuitamente em qualquer smartphone) torna a criação de tarefas e, posteriormente, a exploração de trilhos, muito mais dinâmicos e motivadores para os alunos. Nesta sessão prática, iremos explicar como criar tarefas matemáticas no computador, no portal Math City Map (https://mathcitymap.eu/pt/), usando os guiões criados no âmbito do projeto “Math City Map nas Caldas da Rainha” e explorando fotografias recolhidas pelos alunos. Veremos ainda como criar trilhos matemáticos, unindo as tarefas, e como explorar estes percursos na aplicação Math City Map, no telemóvel. Notas biográficas Manuel João Marques – Licenciado em Matemática Ramo Educacional, pela Faculdade de Ciências da Universidade de Coimbra. Docente de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário, desde 2001, atualmente na Escola Secundária Afonso Lopes Vieira (Leiria). Coautor de manuais escolares do 3.º Ciclo, entre 2001 e 2012. Formador acreditado pelo Conselho Científico-Pedagógico da Formação Contínua, desde 2013. Atualmente, exerce funções na Associação de Professores de Matemática (APM) e é coordenador do Grupo de Trabalho CASIO+ da APM. Dora Vaz Pinto – Licenciada em Matemática (Ramo de Formação Educacional), pela Universidade do Algarve e Pós-Graduada em Matemática Aplicada, pela Universidade Lusíada. Docente de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário, desde 2004, atualmente no Agrupamento de Escolas Raul Proença (Caldas da Rainha). Pedro Mesquita – Licenciado em Matemática (Ramo de Formação Educacional) pela Faculdade de Ciências e Tecnologia da Universidade de Coimbra. Docente de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário, desde 1994. Professor na escola Secundária Rafael Bordalo Pinheiro (ESRBP), desde 1997. Coordenador dos cursos de Educação e Formação de Adultos (EFA). |
SP 08 - A Importância dos projetos STEM nas Novas Aprendizagens de Matemática com a TI-Nspire CX II-TAntónio Vidal, Agrupamento de Escolas Júlio Dantas, Lagos | Grupo T3 Portugal Quarta-feira, 17 de julho, 9h00m - 11h00m Resumo Nesta sessão, serão partilhados e explorados projetos STEM, em consonância com as Novas Aprendizagens Essenciais, onde a tecnologia se torna aliada na aprendizagem dos alunos, estimulando a sua criatividade, incentivam a curiosidade, cultivam o espírito crítico, preparando-os para enfrentarem um futuro cada vez mais científico e tecnológico. As tarefas selecionadas exploram as práticas do pensamento computacional, imprescindíveis na atividade matemática e que proporcionam aos alunos ferramentas que lhes permitem resolver problemas, em especial relacionados com a programação (linguagem Python). Notas biográficas António Vidal – Membro do GT T3 da APM, Professor de Matemática do AE Júlio Dantas Marisabel Antunes – Membro do GT T3 da APM, professora de uma turma experimental de matemática A das novas AE na Escola Secundária D. Dinis. |
SP 09 - Apresentações informais de conceitos e resultados matemáticosAtractor, Associação Atractor – matemática interactiva Terça-feira, 16 de julho, 14h00m - 16h00m Resumo Ao expor conceitos ou resultados matemáticos, antes de proceder a formulações precisas é aconselhável procurar transmitir informalmente as ideias subjacentes a esses conceitos ou resultados. No entanto, a escolha de tais abordagens informais é muito delicada. Por exemplo, a sucessão 1, 1/2, 1/3, 1/4, ... , 1/n, ... é convergente para 0. Quando se quer aproveitar este exemplo para transmitir informalmente o que isto significa, ouve-se com frequência: dizer que “uma sucessão é convergente para zero” significa que (C) os seus termos se vão aproximando cada vez mais de 0. Ora a ideia de convergência é diferente e a condição (C) (satisfeita por aquela sucessão) nem é suficiente nem necessária para a convergência para 0. A sucessão 2/1, 3/2, 4/3, 5/4, ... , (n+1)/n , ... satisfaz a (C) e não converge para 0 e a sucessão ((2+(-1)^n)/n)n converge para 0 e não satisfaz a (C). A sessão procurará envolver os participantes na procura de abordagens informais de alguns conceitos e resultados. Nota: (não necessário, mas desejável) ter um portátil com acesso a Internet. Nota biográfica https://www.atractor.pt |
SP 10 - Geometria Sintética com o GeoGebraJosé Carlos Pereira Terça-feira, 16 de julho, 14h00m - 16h00m Resumo A Geometria Sintética é um dos tópicos das Novas Aprendizagens Essenciais de Matemática A do Ensino Secundário. Nesta Sessão Prática iremos trabalhar algumas tarefas sobre este conteúdo, nomeadamente Pontos Notáveis de um Triângulo, Reta de Euler e Circunferência dos Noves Pontos. Usaremos o GeoGebra para conjeturar algumas das propriedades que envolvem estes conteúdos para, de seguida, as tentarmos provar. Todas as tarefas a realizar poderão ser utilizadas em contexto de sala de aula. Não é necessário ser um utilizador experiente do GeoGebra para poder frequentar esta sessão. Como pré-requisito é apenas necessário saber o processo de construção dos quatro pontos notáveis presentes no Programa, Incentro, Circuncentro, Baricentro e Ortocentro. Nota biográfica José Carlos Pereira – Professor de Matemática, licenciado pela Faculdade de Ciências da Universidade de Lisboa com estágio profissional na Escola Secundária Seomara da Costa Primo. Dedica-se ao seu centro de explicações de Matemática desde então. É administrador do grupo de Facebook Recursos para Matemática, onde gere e fomenta a partilha e discussão de temas relacionados com a Matemática e a sua docência entre mais de 9000 membros. Coautor do livro de apoio escolar Preparar o Exame Matemática A, da Raiz Editora e do manual Matemática 360 da mesma editora. Colaborador do Clube de Matemática da Sociedade Portuguesa de Matemática, com a coluna «Se e só se». |
SP 11 - As pontes entre a Matemática e a sua História nas Aprendizagens Essenciais da MatemáticaTeresa Costa Clain | GHMEM do CIDMA/Universidade de Aveiro Quarta-feira, 17 de julho, 9h00m - 11h00m Resumo O objetivo da sessão proposta é trabalhar os temas transversais, mais concretamente, a História da Matemática nas Aprendizagens Essenciais (AE) homologadas recentemente. Pretende-se: conhecer, manejar e explorar os domínios inerentes às AE; apresentar e interpretar uma variedade de problemas que resultam na utilização dos domínios/temas com inclusão dos temas transversais e utilizando abordagens didáticas diversificadas e auxiliares na exposição dos temas, bem como na elaboração e resolução de exercícios, explorar as potencialidades de alguns recursos tecnológicos na elaboração e resolução de exercícios/atividades relacionados com cada tema. Motiva-se o trabalho colaborativo entre os docentes e a partilha de experiências didáticas, importantes para o desenvolvimento profissional. Serão disponibilizados aos formandos a apresentação da sessão e outros materiais dentro de cada contexto temático (fichas de trabalho, sugestões de atividades, entre outros). Nota: Os participantes devem trazer um computador com o GeoGebra instalado. Nota biográfica Teresa Costa Clain – Docente de Matemática no Agrupamento de Escolas Coimbra Centro, é formadora em Matemática, Didática da Matemática e colaboradora do Grupo de História da Matemática e Educação Matemática do CIDMA da Universidade de Aveiro (UA), onde desenvolve investigação sobre a História da Matemática e as suas aplicações na sala de aula. Participa no Projeto “Histórias com Ciência na Biblioteca Escolar”, da UA e da Rede Nacional de Bibliotecas Escolares. |
SP 12 - Corrida de Carros – usando Python e funções polinomiais e trigonométricasSandra Gaspar Martins | Instituto Superior de Engenharia de Lisboa Terça-feira, 16 de julho, 9h00m - 11h00m Resumo Os meus alunos fazem este trabalho que é uma corrida de carros usando programação em Python. Também pode ser uma joaninha a percorrer um prado verdejante, etc. É muito atrativo para eles. Os alunos escolhem uma pista e um carro de que gostem. Eu forneço aos alunos o programa em que o meu carro percorre a minha pista, eles só alteram para ser o deles a percorrer a pista deles. A parte de Python é simples e já está feita, na prática só têm de manipular a matemática. Os alunos devem conhecer senos e cossenos em radianos e polinómios. Nesta sessão, vou dar um carro, uma pista, e o meu programa Python, e cada um/cada grupo (como preferirem) vai tentar que o carro percorra a pista. Verão que é muito simples! No final entregarei todos os materiais que vos poderão ajudar a implementar este trabalho com os vossos alunos, e ficarei disponível para todo o apoio via zoom ou email. Nota: Deverá trazer um computador com Python instalado. Se não for utilizador de Python ficará num grupo com alguém que seja utilizador – verá que é muito simples. Eu forneço o programa Python e só tem de trabalhar a matemática. Nota biográfica Sandra Gaspar Martins – Docente de matemática do Instituto Superior de Engenharia de Lisboa desde 2000. Foi docente do ensino básico durante 3 anos. É doutorada em Ciências da Educação pela Universidade Nova de Lisboa. Um grande foco do seu trabalho é tirar partido da tecnologia para fomentar a aprendizagem significativa dos alunos. |
SP 13 - Resolução de problemas e pensamento computacionalCélia Mestre, Escola Superior de Educação, Instituto Politécnico de Setúbal Terça-feira, 16 de julho, 9h00m - 11h00m Resumo O pensamento computacional é uma capacidade essencial para a formação do individuo, pois envolve processos de pensamento importantes para a formulação e resolução de problemas. As Aprendizagens Essenciais de Matemática para o Ensino Básico trouxeram novos desafios à prática dos professores, entre eles, o pensamento computacional, enquanto capacidade matemática que requer o desenvolvimento de várias práticas (e.g., abstração, decomposição, reconhecimento de padrões, algoritmia e depuração) através de tarefas matemáticas desafiantes, planificadas e implementadas com intencionalidade. Nesta sessão prática iremos discutir o conceito de “pensamento computacional” e suas práticas à luz da resolução de duas tarefas que exploram conhecimentos sobre números (e.g., paridade, igualdade/desigualdade). Pretendemos igualmente promover a reflexão acerca do tipo de tarefa e atividade matemática que promove o desenvolvimento do pensamento computacional dos alunos na aula de matemática. Notas biográficas Célia Mestre – Exerce funções na Escola Superior de Educação de Setúbal, como professora requisitada. Têm vasta experiência na docência de 1.º ciclo, na formação contínua e na formação inicial de professores no âmbito da Didática da Matemática. É doutorada em Educação, especialidade em Didática da Matemática, pelo Instituto de Educação da Universidade de Lisboa. Possui Pós-Graduação em Tecnologias e Metodologias da Programação no Ensino Básico, pela mesma instituição e tem Mestrado e Licenciatura em Ciências da Educação pela Faculdade de Psicologia e Ciências de Educação da Universidade de Lisboa. A sua formação inicial é Licenciatura em Ensino da Matemática e Ciências da Natureza, pela Escola Superior de Educação de Beja. É coautora das novas Aprendizagens Essenciais de Matemática do Ensino Básico (2021). Renata Carvalho – É licenciada em Ensino na variante de Matemática e Ciências da Natureza pela ESE de Portalegre. Possui Mestrado em Educação na área de Didática da Matemática pela Faculdade de Ciências da Universidade de Lisboa e Doutoramento em Educação, na mesma área, pelo Instituto de Educação da Universidade de Lisboa. Tem colaborado em projetos e encontros nacionais e internacionais na área da Educação Matemática e na formação contínua de professores. Colabora, desde 2016/17 com a ESE de Lisboa na formação inicial de professores. Atualmente é Diretora do Centro de Formação da APM. |
SP 14 - Atribuir significado à divisão: um itinerário para a sala de aula dos naturais às fraçõesMiguel Ribeiro | Universidade Estadual de Campinas (UNICAMP), Brasil Quarta-feira, 17 de julho, 9h00m - 11h00m Resumo Os resultados dos alunos estão ainda “longe do esperado” em diversos tópicos e competências matemáticas, o que nos informa, por um lado sobre um conjunto de dificuldades a matemática e, por outro, da necessidade de uma discussão na formação de professores que nos possibilite práticas matemáticas que transformem esses conhecimentos matemáticos. Entre esses tópicos matemáticos a divisão e as frações são identificados como dois dos “mais problemáticos”, aumento essas dificuldades quando os conjugamos: divisão de frações. Promover essa compreensão exige passar a conhecer e entender as conexões desses tópicos com a medida, levando a generalizar processos e formas de Pensar matematicamente que são empregues nos naturais expandindo-os para as frações. Nesta sessão prática iremos vivenciar um itinerário de discussões matemáticas modelando a prática que amplia o espaço de entendimento sobre a divisão e as frações, erradicando as dificuldades dos alunos e desenvolvendo as suas competências de forma que possam generalizar as formas de proceder e pensar matematicamente a outros tópicos. Nota biográfica Miguel Ribeiro – Doutor em Didática da Matemática pela Universidade de Huelva (Espanha), formador de professores com foco nas especificidades da prática e conhecimento do professor e atualmente Professor na UNICAMP (Brasil). |
SP 15 - Descobrir volumes em embalagens e outras que taisIsabel Costa Belo | Agrupamento de Escolas Martim de Freitas - Coimbra Terça-feira, 16 de julho, 9h00m - 11h00m Resumo As tarefas matemáticas apresentadas, “Vamos descobrir o volume a partir de embalagens”, “As compras da Maria” e “Cápsulas de café”, tendo como objetivos promover e aliciar o interesse dos alunos; dando oportunidade de aprofundar conceitos previamente introduzidos; desenvolver e aperfeiçoar as capacidades matemáticas dos alunos e permitir que descrevam, ampliem, criem, analisem as questões em cada tarefa, promover a comunicação matemática e desenvolver nos alunos a capacidade de explorar e raciocinar logicamente. Os momentos de trabalho em grupo e de discussão em grande grupo são fundamentais para a compreensão e revisão de conceitos, onde os alunos têm a oportunidade de aprender a justificar oralmente e por escrito os seus raciocínios e procedimentos, beneficiando os alunos na aprendizagem e na construção ativa dos conhecimentos. A tarefas propostas promovem a oportunidade de resolver diferentes questões com capacidades matemáticas diversificadas, utilizando diversas estratégias com recurso a embalagens, velas, régua e calculadora, permitindo o desenvolvimento da linguagem matemática. Ao aprenderem estratégias de resolução diversificadas, os alunos desenvolvem a argumentação, conjeturam, generalizam e justificam raciocínios, adquirindo de forma progressiva a formalização. Nota biográfica Isabel Costa Belo – Licenciada em Ensino da Matemática e Ciências Naturais. Mestre em Matemática pela Universidade de Aveiro. Possui uma Formação Especializada em Administração e Organização Escolar. Colaboradora com a Universidade de Coimbra no Projeto Europeu Clohe. Autora de livros na área da Matemática. Autora e Colaboradora em Publicações, Comunicações e Projetos na área da Educação. Tem formação em Comprehensive School Mathematics Program. Cooperante em Estágios de Mestrado na Matemática. |
SP 16 - A aprendizagem de Geometria com o GeoGebraMariana Ribeiro | António Domingos | Helder Martins Quarta-feira, 17 de julho, 9h00m - 11h00m Resumo As Novas Aprendizagens Essenciais de Matemática A preveem a utilização de ambientes de Geometria Dinâmica. O objetivo desta sessão é mostrar como o GeoGebra pode ser uma ferramenta muito útil no ensino e aprendizagem de Geometria, nomeadamente, por permitir aos alunos visualizar e manipular os objetos matemáticos em estudo, e, como tal, estimulá-los a fazerem as suas próprias conjeturas. Nesta sessão, iremos fazer uma pequena partilha sobre os resultados de uma investigação acerca da influência do GeoGebra na aprendizagem do tema Geometria Sintética. De seguida, iremos realizar algumas tarefas práticas sobre Pontos Notáveis de um Triângulo, Reta de Euler, Circunferência dos nove pontos e Geometria Analítica no Espaço, que poderão ser implementadas nas vossas aulas. Todos são bem-vindos na sessão, mesmo quem ainda não tenha tido muito contacto com o GeoGebra. Notas biográficas Mariana Fernandes Ribeiro – Aluna finalista do Mestrado de Ensino da Matemática da NOVA-FCT, a frequentar o estágio profissional na Escola Secundária António Damásio com uma turma piloto das Aprendizagens Essenciais de 2023. Em 2022, licenciou-se em Matemática pela FCUL. Tendo-se dedicado às explicações de Matemática desde 2021. António Domingos – Professor Auxiliar do Departamento de Ciências Sociais Aplicadas, da NOVA-FCT, licenciado em Matemática e Desenho, com mestrado e doutoramento em Ciências da Educação, na especialidade de Teoria e Desenvolvimento Curricular. Leciona na NOVA-FCT, no Mestrado em Ensino da Matemática, no Mestrado em Educação, e no Programa Doutoral em Educação. É coautor das Aprendizagens Essenciais de 2023, bem como de vários artigos publicados em revistas nacionais e internacionais relacionados com STEM. Tem orientado várias dissertações de mestrado e doutoramento. Helder Manuel Martins – Licenciado em Ensino da Matemática, pela FCUL; mestre em Educação, especialidade de STEM, pela FCT NOVA; e Doutorando em Educação, Inovação Educativa, pela FCT/FCSH/ISPA. É professor na Escola Secundária António Damásio, desde 1992, tendo igualmente acumulado funções em diversos colégios privados da área da grande Lisboa. É orientador de estágios a formandos do curso de Mestrado em Ensino de Matemática no 3.º ciclo do Ensino Básico e no Secundário da FCT NOVA, desde 2020, e é classificador e supervisor da classificação de exames de Matemática A, desde 2003. Colaborou nos projetos T3 – Teaching Teachers with Technology, da APM, e REANIMAT, da FCUL e da FCG, tendo igualmente publicado artigos em revistas e em livros de atas de diversos encontros e congressos de educação. É coautor de manuais escolares de Matemática para o Ensino Secundário; é coautor do relatório “Recomendações para a melhoria das aprendizagens dos alunos em Matemática”; e, coautor e formador das novas Aprendizagens Essenciais para a Matemática do Ensino Secundário. |
SP 17 - Tarefas de Modelação – O foco nas ações do professorAntónio Júlio Aroeira | Escola Básica e Secundária da Madalena Terça-feira, 16 de julho, 9h00m - 11h00m Resumo As Aprendizagens Essenciais de Matemática seguem a tendência internacional na relevância atribuída à modelação matemática no processo de ensino e aprendizagem dos alunos, nomeadamente no desenvolvimento de competências de compreensão e intervenção num mundo cada vez mais complexo e tecnológico. As competências de modelação matemática dos alunos podem ser efetivamente promovidas, tendo em atenção um equilíbrio necessário entre a orientação do professor e independência do trabalho alunos. Nesta sessão prática, tomaremos como ponto de partida a resolução de uma tarefa de modelação, considerando as possíveis resoluções, antecipando as dificuldades dos alunos e as possíveis ações do professor. Com a discussão sobre a tarefa proposta pretendemos caracterizar o que é uma boa tarefa de modelação, as etapas do ciclo de modelação, o papel da tecnologia e as competências promovidas pelas tarefas de modelação, tomando como referências as AE. Nota: Os participantes devem ser portadores de uma calculadora gráfica. Notas biográficas António Júlio Aroeira – Professor de Matemática, Licenciado em Matemática (via Ensino) pela Faculdade de Ciências da Universidade de Lisboa. Atualmente leciona na Escola Básica e Secundária da Madalena. Integrou a equipa de Acompanhamento Local do Programa de Matemática (1998-2022) e mais recentemente a equipa de Formação e Acompanhamento do Ensino Básico na R. A. dos Açores (2013-2021). Susana Carreira – Professora Associada da Faculdade de Ciências e Tecnologia da Universidade do Algarve; Professora Associada Convidada do Instituto de Educação da Universidade de Lisboa. Desenvolve investigação sobre modelação no ensino e aprendizagem da matemática; tem publicações nacionais e internacionais neste domínio, bem como orientações de dissertações e teses. Tem participado em conferências internacionais com foco no tema, como o ICTMA e o CERME (no Topic Working Group on Applications and Modelling). |
SP 18 - Estatística - Análise De Dados E Representações Gráficas Com O GeogebraMaria José Teixeira Do Nascimento | Escola Secundária São Pedro Terça-feira, 16 de julho, 14h00m - 16h00m Resumo O recurso tecnológico do software de matemática dinâmica GeoGebra, é um instrumento importante para a prática do professor, no sentido de redesenhar a forma como se ensina e de desenvolver estratégias que envolvam e predisponham os alunos para uma aprendizagem significativa. A utilização do GeoGebra permite uma abordagem de conteúdos matemáticos, através da experimentação e da manipulação dinâmica de diferentes elementos, facilitando a realização de construções para deduzir resultados e propriedades a partir da observação direta. Esta Sessão prática inscreve-se na necessidade capacitar os professores dos grupos 230 e 500 para a operacionalização das novas Aprendizagens Essenciais de Matemática para o Ensino Básico e Ensino Secundário, no Tema Dados e Probabilidades, particularmente na análise de dados (Análise Univariada, Análise Bivariada, e cálculo de estatísticas) e representações gráficas (Gráficos de linha, Gráficos Circulares, Histogramas e Diagramas de extremos e quartis). Pretende-se que os professores adquiram alguma destreza e predisposição para a sua integração na prática letiva. Nota: Os participantes na sessão prática deverão trazer um portátil. Nota biográfica Maria José Teixeira Do Nascimento – Professora do grupo 500. Licenciada em Matemática (Ensino) pela Faculdade de Ciências e Tecnologia da Universidade de Coimbra (FCTUC); Mestre em Ensino da Matemática pela Universidade de Trás-os-Montes e Alto Douro (UTAD); Certificada como formadora nas áreas e domínios: Matemática/Métodos Quantitativos e Didáticas Específicas (Matemática); É Formadora no CFAEATB. Participou na capacitação de formadores das novas AE em Matemática do Ensino Básico, e foi formadora no âmbito das AE de Matemática para o 2.º ciclo. É docente na Escola Secundária de São Pedro, em Vila Real. |
SP 19 - O Software Intuitivo – Avaliações em Formato DigitalFilipa Susana da Graça Ferreira | Agrupamento de Escolas José Afonso, Alhos Vedros Terça-feira, 16 de julho, 9h00m - 11h00m Resumo A crescente adoção do Intuitivo reflete a tendência de digitalização no setor educacional e a busca por soluções que proporcionem uma maior eficiência e qualidade nas avaliações. A utilização deste software pelos docentes, possibilita a realização de avaliações em formato digital, bem como a partilha de materiais entre pares. Pretende-se dar a conhecer as potencialidades e os constrangimentos de utilização desta ferramenta, contribuir para criar e administrar avaliações de forma digital, permitindo o acompanhamento do progresso dos alunos, de forma mais ecológica e com a automatização de algumas correções de exercícios. A crescente adoção do Intuitivo reflete a tendência de digitalização no setor educacional e a busca por soluções que proporcionem uma maior eficiência e qualidade nas avaliações. Nota: Os participantes na sessão prática deverão ter computador, tablet ou iPad. Nota biográfica Filipa Susana da Graça Ferreira – Licenciada em matemática (ramo educacional) e com um curso de especialização em supervisão pedagógica, é atualmente Professora no AE José Afonso, em Alhos Vedros e Assistente Convidada na Escola Superior de Tecnologia de Setúbal - IPS. Ao longo da sua vida profissional tem tentado contribuir na modernização de processos de avaliação, na melhoria da experiência de alunos e professores, e na integração de tecnologias digitais que sejam facilitadoras do processo de ensino-aprendizagem. |
SP 20 - Eu e o mundo, a maldita matemática e outras histórias – uma abordagem interdisciplinar entre a literatura infantojuvenil e a matemáticaSusana Colaço | Maria Clara Martins Terça-feira, 16 de julho, 14h00m - 16h00m Resumo Esta sessão prática tem como objetivo integrar a literatura infantojuvenil no ensino da matemática do 1.º e 2.º ciclos, abordando tópicos de temas matemáticos como geometria e medida, organização e tratamento de dados, números e operações e álgebra. Pretende-se proporcionar aos participantes uma abordagem interdisciplinar recorrendo a exemplos de literatura infantojuvenil para fortalecer as aprendizagens essenciais em Matemática nestes dois ciclos de ensino, nomeadamente, no que diz respeito à compreensão matemática dos alunos e ao desenvolvimento de capacidades matemáticas e competências transversais gerais associadas aos temas matemáticos. A partir de uma metodologia ativa, os participantes terão oportunidade de criar e realizar tarefas práticas tendo como ponto de partida narrativas infantojuvenis e refletindo também sobre aprendizagem dos alunos, o papel do professor e o papel do aluno no desenvolvimento de um trabalho interdisciplinar desta natureza. Notas biográficas Susana Colaço – Professora Coordenadora na Escola Superior de Educação - Instituto Politécnico de Santarém. Licenciada em Matemática, Mestre e Doutorada também em Matemática pela Universidade de Lisboa e Especialista em Formação de Professores do Ensino Básico do 1.º e 2.º Ciclos. Há mais de 25 anos é formadora de professores e educadores, quer no âmbito da formação inicial, quer na formação contínua. As suas áreas de interesse vão desde a utilização da Tecnologia no Ensino da Matemática à Didática da Matemática, em particular para os primeiros anos a áreas mais abrangentes como a Inclusão e a Sustentabilidade na formação de futuros Professores. Maria Clara Martins – Professora na Escola Superior de Educação-Instituto Politécnico de Santarém. Especialista em Formação de Professores do Ensino Básico do 1.º e 2.º Ciclos. Licenciada em Matemática pela Universidade de Coimbra e Mestre em Matemática para o Ensino pela mesma universidade. As suas áreas de interesse são a Didática da Matemática e a Formação de professores em Matemática dos primeiros anos com incidência na abordagem STEAM, interdisciplinaridade e articulação curricular e recursos manipuláveis e digitais em educação. |
SP 21 - Explorando a Geometria com o Scratch: Uma abordagem prática para professores de MatemáticaNuno Raínho | Carlos Leão Quarta-feira, 17 de julho, 9h00m - 11h00m Resumo Esta sessão prática é projetada para professores de Matemática que desejam integrar o pensamento computacional nas suas aulas através do Scratch, metodologia que está em consonância com os objetivos das Aprendizagens Essenciais para os 2.º e 3.º ciclos. O uso do Scratch apoia o desenvolvimento do pensamento computacional, essencial para a resolução de problemas, e facilita a criação de múltiplas representações dos conceitos. Além disso, promove a exploração de conexões entre diferentes áreas da Matemática e a aplicação de conceitos em contextos reais, proporcionando uma visão integrada da disciplina. Durante a sessão, os professores terão a oportunidade de se familiarizar com a interface do Scratch e de explorar como a programação pode ser usada para explorar matemática de maneira criativa e envolvente, neste caso especialmente dedicada à geometria e medida. Nota: Esta sessão também poderá interessar a outros níveis do ensino. Os participantes na sessão prática deverão ter computador ou tablet ou iPad. Notas biográficas Nuno Raínho – Docente de Matemática no Agrupamento de Escolas Tondela Cândido Figueiredo e Assistente Convidado na ESECS-IPL. É também colaborador no projeto “O pensamento computacional na formação inicial de professores dos primeiros anos” do CI&DEI do IPL. Dinamizador dos projetos Desafios e Matematrix da ESECS-IPL. Carlos Leão – Coordenador do Departamento de Ciências Exatas, Naturais e Tecnológicas e docente de Matemática no Colégio Rainha Dona Leonor, Caldas da Rainha e Assistente Convidado na ESECS-IPL. É também colaborador e dinamizador do projeto Matematrix da ESECS-IPL. |
ProfMat 2024 - Simpósios de Comunicações (1h)
Os simpósios são espaços para a apresentação de comunicações (15 minutos cada), que divulgam experiências, projetos, trabalhos, investigações ou outras intervenções com relevância na Educação Matemática. Têm uma duração global que permite a apresentação das comunicações e um tempo de discussão, para que a audiência possa formular questões, no final das apresentações.
Simpósio de Comunicações 01 (SC 01)
Coisas que aconteceram... Episódios do passado de ensino da Matemática
Moderador: Rui Candeias
Quarta-feira, 17 de julho, 9h00 - 10h00
Auditório da E. S. Rafael Bordalo Pinheiro
| A |
1964: Os 60 anos do projeto Sebastião e Silva (Resumo) José Manuel Matos, Universidade Nova de Lisboa Público: SECUNDÁRIO |
| B |
A Matemática Moderna no ensino primário: a introdução da teoria dos conjuntos (Resumo) Rui Candeias, Agrupamento de Escolas Terras de Larus Público: 1.º CICLO |
| C |
Matemática Recreativa - Geometrias Não Euclidianas no Ensino Secundário (Resumo) Maria Teresa Serrão Sanches Gonçalves, Escola Básica e Secundária Ribeiro Sanches Público: SECUNDÁRIO |
Simpósio de Comunicações 02 (SC 02)
Moderador: João Terroso
Terça-feira, 16 de julho, 11h30 - 12h30
E. S. Rafael Bordalo Pinheiro, Bloco 2, Piso 2, Sala 20
|
A B C |
Apps for Good – Metodologia de projeto inovadora (Resumo) Matilde Buisel | Sara Cordeiro | Paula Fernandes Público: GERAL |
Simpósio de Comunicações 03 (SC 03)
Moderadora: Susana Carreira
Quarta-feira, 17 de julho, 9h00 - 10h00
Pequeno Auditório do CCC
| A |
Trabalho de projeto na aula de Matemática (Resumo) Nélia Amado, Universidade do Algarve Público: 3.º CICLO e SECUNDÁRIO |
| B |
Biomatemática no ensino profissional (Resumo) Alexandra Rodrigues, CICS.NOVA, Faculdade de Ciências e Tecnologia da Universidade NOVA de Lisboa, UIED Público: SECUNDÁRIO |
Simpósio de Comunicações 04 (SC 04)
Moderadora: Dina Tavares
Terça-feira, 16 de julho, 15h00 - 16h00
Grande Auditório do CCC
| A |
Avaliações diversificadas - um contributo (Resumo) Belarmina Cristina Azevedo | Luisa Adelina Selas | Manuel Teles Lagido Público: 3.º CICLO e SECUNDÁRIO |
| B |
“Mas, já temos a resposta do problema, o que temos de fazer agora?” – uma abordagem indo além de encontrar a resposta (Resumo) Miguel Ribeiro, Universidade Estadual de Campinas (UNICAMP), Brasil Público: GERAL |
| C |
Quizzes no moodle – momentos com todos os alunos atentos e focados (Resumo) Sandra Gaspar Martins | Instituto Superior de Engenharia de Lisboa Público: GERAL |
Simpósio de Comunicações 05 (SC 05)
Moderador: Carlos Leão
Terça-feira, 16 de julho, 11h30 - 12h30
E. S. Rafael Bordalo Pinheiro, Bloco 2, Piso 2, Sala 19
| A |
Rumo ao Dragão: as Capacidades Matemáticas no nosso quotidiano (Resumo) Jéssica Silva | João Tiago Dos Santos Gonçalves | Dárida Maria Fernandes Público: 1.º CICLO |
| B |
A promoção da educação financeira por meio das aprendizagens essenciais: um olhar para a matemática no salário (Resumo) Reullyanne Freitas de Aguiar | Alexandra Sofia da Cunha Rodrigues | Francisco Alexandre de Lima Sales | Raimundo Luna Neres Público: GERAL |
| C |
Interlocução Coletiva na construção das Aprendizagens Essenciais de Matemática (Resumo) Helena Gil Guerreiro | Susana Brito Público: 1.º CICLO |
Simpósio de Comunicações 06 (SC 06)
Moderador: Manuel João Marques
Terça-feira, 16 de julho, 15h00 - 16h00
Pequeno Auditório do CCC
|
A B C |
Math City Map – Trilhos matemáticos nas Caldas da Rainha (Resumo) Dora Vaz Pinto, Escola Secundária Raul Proença Público: GERAL |
Simpósio de Comunicações 07 (SC 07)
Moderador: António Vidal
Terça-feira, 16 de julho, 11h30 - 12h30
E. S. Rafael Bordalo Pinheiro, Bloco 2, Piso 2, Sala 16
| A |
A Modelação como estratégia de ensino da Matemática (Resumo) Ana Lopes | Alexandra Rodrigues Público: 3.º CICLO e SECUNDÁRIO |
| B |
Centro de estudos em História da Matemática e Educação Científica (Resumo) Teresa Costa Clain, GHMEM do CIDMA/Universidade de Aveiro Público: GERAL |
| C |
O que pensam alunos do ensino básico sobre os trabalhos para casa (Resumo) Cristina Fernandes | Manuel Vara Pires Público: BÁSICO |
Simpósio de Comunicações 08 (SC 08)
Moderadora: Alexandra Sofia Rodrigues
Terça-feira, 16 de julho, 15h00 - 16h00
Auditório da E. S. Rafael Bordalo Pinheiro
| A |
Uma visão da Matemática no currículo das Escolas Europeias (Resumo) Paula Gomes, Escola Europeia de Bruxelas II/Escola Secundária de Vila Verde Público: 3.º CICLO e SECUNDÁRIO |
| B |
ContinueUP - conectando a formação inicial e a formação contínua de professores (Resumo) José Miguel Sousa, Secretaria Regional da Educação, Ciência e Tecnologia – Madeira Público: GERAL |
Simpósio de Comunicações 09 (SC 09)
Moderadora: Helena Castro
Quarta-feira, 17 de julho, 9h00 - 10h00
E. S. Rafael Bordalo Pinheiro, Bloco 2, Piso 2, Sala 15
| A |
Laboratório de Matemática- passagem do 1.º para 2.º ciclo- Dia do Agrupamento (Resumo) Virgínia Fernanda das Neves Ferreira | Agrupamento de Escolas António Nobre, Porto Público: 1.º CICLO e 2.º CICLO |
| B |
Problema de Fermi no âmbito do projeto de Flexibilidade Curricular no 8.º ano de escolaridade (Resumo) Manuela Subtil | Agrupamento de Escolas Fragata do Tejo / Escola Superior de Educação de Lisboa Público: 3.º CICLO |
RESUMOS
SC 01 | A – 1964: Os 60 anos do projeto Sebastião e SilvaJosé Manuel Matos | Universidade Nova de Lisboa Quarta-feira, 17 de julho, 9h00m - 10h00m Resumo Em 1964 iniciou-se o projeto de introdução da Matemática Moderna nos últimos anos dos liceus portugueses. Coordenado por Sebastião e Silva e apoiado pelo Governo português e pela OCDE, constitui, ainda hoje, uma das reformas curriculares portuguesas mais importantes. As suas propostas destinadas a alunos escolhidos e consolidadas nos livros de texto do projeto, vão influenciar até meados da década de 90 o ensino da matemática naqueles anos terminais. Esta comunicação, baseada em artigos de jornais da época, fará uma revisão dos seus primórdios e do seu desenvolvimento até 1969, quando as condições de aplicação da reforma se vão alterar significativamente. Serão mencionados os seus participantes mais ativos, as suas produções, e a visão que dela tinham os governantes. Nota biográfica José Manuel Matos – Iniciou a sua carreira na Escola do Magistério de Beja e foi professor de matemática do ensino secundário. Concluiu o mestrado na Universidade de Boston em 1985 e o doutoramento na Universidade da Geórgia em 1999. Lecionou na Faculdade de Ciências e Tecnologia, UNL e na Universidade Federal de Juiz de Fora, Brasil. Desempenhou cargos na APM, na SPCE e na SPIEM. Interessa-se atualmente pelas dimensões sociais, culturais e históricas do ensino e da aprendizagem da matemática. |
SC 01 | B – A Matemática Moderna no ensino primário: a introdução da teoria dos conjuntosRui Candeias | Agrupamento de Escolas Terras de Larus Quarta-feira, 17 de julho, 9h00m - 10h00m Resumo Nesta comunicação pretende-se analisar a forma como o tema da teoria dos conjuntos foi introduzido no ensino da matemática no primário em Portugal, nomeadamente nos programas do ensino primário oficial e nos manuais escolares, desde a década de 1960 até à década de 1990. O período cronológico em estudo coincide com um movimento no interior do ensino da Matemática, o Movimento da Matemática Moderna. Nota biográfica Rui Candeias – Rui Candeias é professor do 1.º ciclo do ensino básico, no Agrupamento de Escolas Terras de Larus e investigador. O principal interesse de investigação centra-se na história da educação matemática, particularmente na formação de professores e desenvolvimento curricular. Nesta área, concluiu a sua tese de doutoramento em 2021, na FCT/UNL. Faz parte do Grupo de Trabalho sobre História e Memórias do Ensino da Matemática (GTHMEM), da Associação de Professores de Matemática, desde a sua formação. |
[Início_SC]
SC 01 | C – Matemática Recreativa - Geometrias Não Euclidianas no Ensino SecundárioMaria Teresa Serrão Sanches Gonçalves | Escola Básica e Secundária Ribeiro Sanches Quarta-feira, 17 de julho, 9h00m - 10h00m Resumo Porque não aproveitar o espaço, o momento e o grupo de alunos num clube de Matemática para propor a realização de tarefas muito específicas e de forma recreativa abordar as Geometrias não euclidianas e consequentemente “observar” o que é “dito”? Foi num clube de Matemática que um pequeno grupo de alunos foi confrontado com propostas didáticas cujo propósito foi o de “fazer emergir sinais”, expressos na linguagem, de tal modo que estes pudessem ser identificados como indiciadores de uma atividade intelectual conducente (que evolui até) à apropriação de significados geométricos. Com base na Teoria da Mediação Semiótica (TMS) realizou-se um estudo focado na evolução da construção de significados matemáticos, em que a análise foi feita a partir da emergência e evolução de sinais. Nesta comunicação apresentaremos uma parte do estudo, centrando-nos numa abordagem que relaciona a parte recreativa da matemática com o ensino e a aprendizagem da disciplina. Nota biográfica Maria Teresa Serrão Sanches Gonçalves – Licenciada em Ensino de Matemática e doutorada em Didática da Matemática pela Universidade da Beira Interior. Exerce funções docentes na EB e Secundária Ribeiro Sanches. Integra o Grupo de Trabalho sobre História e Memórias do Ensino da Matemática da APM. Os seus principais interesses de investigação prendem-se com questões ligadas à Didática da Geometria, especificamente as metodologias no ensino (aprendizagem) da Geometria e à Geometria na História da Educação Matemática. |
[Início_SC]
SC 02 – Apps for Good – Metodologia de projeto inovadoraMatilde Buisel | Sara Cordeiro | Paula Fernandes Terça-feira, 16 de julho, 11h30m - 12h30m Resumo O Apps for Good é um programa educativo tecnológico que oferece às escolas uma metodologia de projeto assente no contexto curricular, cujo processo de aprendizagem é centrado no aluno e, onde o professor é convidado a adotar o papel de facilitador. Notas biográficas Matilde Buisel – Mestre em Psicologia Clínica pela Universidade ISPA – Instituto Universitário de Ciências Psicológicas, Sociais e da Vida – em Lisboa. Fez o seu estágio em psicologia na clínica CADIN e é membro efetivo da Ordem dos Psicólogos. Trabalha no CDI Portugal como gestora de projeto do programa educativo tecnológico internacional Apps for Good. Fez um curso em Project Management em Nova Orleães com certificação pelo Project Management Institute (PMI) e participou num Bootcamp sobre impacto social e inovação, promovido pelo European Investment Bank Institute e Faculdade Católica de Lisboa. É também certificada em Competências Pedagógicas (CPP). No Apps for Good, tem gerido e acompanhado o arranque e a implementação do programa em Portugal desde o início. Sara Cordeiro – Mestre em Psicologia da Saúde e Reabilitação Neuropsicológica, pela Universidade de Aveiro. Realizou estágios em contexto hospitalar e participou na organização da 10ª edição das Jornadas da Psicologia enquanto Coordenação do Núcleo de Estudantes de Psicologia. Paula Fernandes – Responsável de avaliação do impacto. Licenciada (pré-Bolonha) em Psicologia Clínica, na Variante Clínica e do Aconselhamento, pela ULHT de Lisboa e Pós-Graduada com Especialização em Terapias Comportamentais e Cognitivas, na APTCC. Orientadora de estágio profissional para a OPP. Atualmente é formadora de projetos no CDI Portugal e responsável pela avaliação do impacto. |
[Início_SC]
SC 03 | A – Trabalho de projeto na aula de MatemáticaNélia Amado | Universidade do Algarve Quarta-feira, 17 de julho, 9h00m - 10h00m Resumo Podemos definir o Trabalho de Projeto como uma metodologia de aprendizagem que envolve os alunos na aprendizagem de conhecimentos e no desenvolvimento de competências através de um processo de investigação alargado, estruturado em torno de questões complexas e autênticas, que deve ser cuidadosamente planeado e cujo produto final deve ser apresentado e divulgado junto da comunidade. A ideia subjacente ao Trabalho de Projeto, em matemática, é a de proporcionar aos alunos uma oportunidade para aprender, dentro e fora da sala de aula, sobre temas relevantes de diversas áreas, de forma integrada e do seu interesse, de acordo com o Perfil dos Alunos à saída da Escolaridade Obrigatória. As atuais Aprendizagens Essenciais de Matemática, consideram que deve ser desenvolvido pelo menos um Trabalho de Projeto no 10.º ano e no 11.º ano de escolaridade. Nesta comunicação apresentamos alguns exemplos de operacionalização do Trabalho de Projeto, destacando algumas vantagens e dificuldades que podem surgir. Notas biográficas Nélia Amado – Doutora em Matemática, especialidade de Didática da Matemática pela Universidade do Algarve. É docente da Faculdade de Ciências e Tecnologia da Universidade do Algarve. Integrou a Comissão de Acompanhamento do Plano da Matemática I e II. Foi consultora científica do Projeto ProSucesso na região Autónoma dos Açores. A formação de professores, resolução de problemas, aspetos afetivos no ensino e aprendizagem da matemática e avaliação em matemática são os seus interesses principais. Alexandra Rodrigues – Doutora em Didática da Matemática pela Universidade da Beira Interior. Tem uma Especialização em Inovação e criatividade – as TIC e outra em Administração e Gestão Escolar. É professora da Faculdade de Ciências e Tecnologia da Universidade NOVA de Lisboa. Os interesses de investigação são diversificados, privilegiando a história da educação e o ensino e a aprendizagem da matemática no ensino profissional. |
[Início_SC]
SC 03 | B – Biomatemática no ensino profissionalAlexandra Rodrigues | CICS.NOVA, Faculdade de Ciências e Tecnologia da Universidade NOVA de Lisboa, UIED Quarta-feira, 17 de julho, 9h00m - 10h00m Resumo Nas Aprendizagens Essenciais de Matemática dos Cursos Profissionais, homologadas em 2023, o módulo opcional OP17 designa-se por Biomatemática. Neste módulo são trabalhados três temas: 1) efeito de escala, 2) crescimento das plantas e Fibonacci e 3) autómatos celulares. Nesta comunicação iremos apresentar duas propostas de tarefas para os dois primeiros temas, ambas para resolver com recurso à tecnologia. Para trabalhar o tema 1) efeito de escala iremos trabalhar a importância da alometria no estudo de espécies biológicas, no tema 2) crescimento das plantas e Fibonacci pretendemos desenvolver uma tarefa para conhecer a importância e aplicações da sucessão de Fibonacci, investigando a sua presença na natureza. Notas biográficas Alexandra Rodrigues – Doutora em Didática da Matemática pela Universidade da Beira Interior. Tem uma Especialização em Inovação e criatividade – as TIC e outra em Administração e Gestão Escolar. É professora da Faculdade de Ciências e Tecnologia da Universidade NOVA de Lisboa. Os interesses de investigação são diversificados, privilegiando a história da educação e o ensino e a aprendizagem da matemática no ensino profissional. Nélia Amado – Doutora em Matemática, especialidade de Didática da Matemática pela Universidade do Algarve. É docente da Faculdade de Ciências e Tecnologia da Universidade do Algarve. Integrou a Comissão de Acompanhamento do Plano da Matemática I e II. Foi consultora científica do Projeto ProSucesso na região Autónoma dos Açores. A formação de professores, resolução de problemas, aspetos afetivos no ensino e aprendizagem da matemática e avaliação em matemática são os seus interesses principais. |
[Início_SC]
SC 04 | A – Avaliações diversificadas – um contributoBelarmina Cristina Azevedo | Luisa Adelina Selas | Manuel Teles Lagido Terça-feira, 16 de julho, 15h00m - 16h00m Resumo Indo ao encontro das áreas de competências definidas nas Aprendizagens Essenciais e o Perfil dos Alunos à Saída da Escolaridade o professor terá de assumir um papel inovador, promotor de aprendizagens significativas e do desenvolvimento de competências utilizando a tecnologia. Na avaliação devemos utilizar procedimentos, técnicas e instrumentos diversificados e adequados às finalidades, ao objeto em avaliação, aos alunos e ao tipo de informação a recolher, que variam em função da diversidade e especificidade do trabalho curricular a desenvolver com os alunos. Aqui faremos a apresentação do trabalho implementado na sala de aula, com alunos do 9º e 11.º anos. Partilharemos convosco as propostas de trabalhos que foram apresentadas aos alunos, os critérios de avaliação aplicados e alguns dos trabalhos em vídeos, jogos e posters digitais realizados pelos alunos. Notas biográficas Belarmina Cristina Azevedo – Professora na Escola Secundária José Régio de Vila do Conde Luisa Adelina Selas – Professora na Escola Secundária José Régio de Vila do Conde Manuel Teles Lagido – Professor na Escola Secundária José Régio de Vila do Conde |
[Início_SC]
SC 04 | B – “Mas, já temos a resposta do problema, o que temos de fazer agora?” – uma abordagem indo além de encontrar a respostaMiguel Ribeiro | Universidade Estadual de Campinas (UNICAMP), Brasil Terça-feira, 16 de julho, 15h00m - 16h00m Resumo Apesar de ser um tema que tem sido discutido nas últimas décadas e fazer parte dos documentos oficiais, a resolução de problemas é ainda algo difícil para os alunos e quando conseguem resolver um determinado problema muitas vezes têm, dificuldades em outro de outro tipo quando se muda o contexto, o que se associa a uma dificuldade mais geral associada à generalização de processos e de formas de pensar matematicamente. Nesse sentido, para além de ser importante que os alunos resolvam problemas (muitos!) é fundamental também que possam formular problemas e desenvolvam o seu conhecimento e competências que lhes permitam navegar entre distintos tópicos e resolver um mesmo problema de distintas formas, explicitando essas diferentes formas de pensar matematicamente. Nesta comunicação, partindo de um conjunto de trabalhos que temos desenvolvido no CIEspMat, e a partir de exemplos da sala de aula, irei discutir alguns problemas e abordagens didáticas emocionantes e que são simultaneamente matematicamente inovadoras, por nos permitirem fazer o que ainda não foi feito, maximizando o entendimento matemático dos alunos. Nota biográfica Miguel Ribeiro – Doutor em Didática da Matemática pela Universidade de Huelva (Espanha), formador de professores com foco nas especificidades da prática e conhecimento do professor e atualmente Professor na UNICAMP (Brasil). |
[Início_SC]
SC 04 | C – Quizzes no moodle – momentos com todos os alunos atentos e focadosSandra Gaspar Martins | Instituto Superior de Engenharia de Lisboa Terça-feira, 16 de julho, 15h00m - 16h00m Resumo Os quizzes do moodle são uma ferramenta que fomenta o envolvimento de todos os alunos em momentos de aprendizagem. Quando há um quiz todos os alunos ficam atentos e empenhados. Os quizzes do moodle são fáceis de construir e podem ser reutilizados nos anos futuros. Estes quizzes são muito adaptados para o ensino da matemática, sendo simples fazer perguntas de matemática. Nesta sessão veremos que podemos escrever texto matemático e incluir gráficos. Destacamos ainda as perguntas de resposta numérica, escolha múltipla e questões embutidas. Nas questões embutidas existem várias questões para completar ao longo de um texto, permitindo ir guiando o aluno ao longo “do caminho”, não querendo apenas uma resposta final. Existem ainda as perguntas de geração aleatória que permitem uma pergunta com valores diferentes para cada aluno. Podem ser usados como TPC ou como questão-aula (funcionam muito bem no telemóvel). Nota biográfica Sandra Gaspar Martins – Docente de matemática do Instituto Superior de Engenharia de Lisboa desde 2000. Foi docente do ensino básico durante 3 anos. É doutorada em Ciências da Educação pela Universidade Nova de Lisboa. Um grande foco do seu trabalho é tirar partido da tecnologia para fomentar a aprendizagem significativa dos alunos. |
[Início_SC]
SC 05 | A – Rumo ao Dragão: as Capacidades Matemáticas no nosso quotidianoJéssica Silva | João Tiago Dos Santos Gonçalves | Dárida Maria Fernandes Terça-feira, 16 de julho, 11h30m - 12h30m Resumo Este trabalho incide sobre as Capacidades Matemáticas das Aprendizagens Essenciais de Matemática de 2021, dando maior relevância à resolução de problemas e ao pensamento computacional. Este estudo surgiu na Unidade Curricular de Didática da Matemática no 1.º Ciclo do Ensino Básico (CEB) do 1.º ano do Mestrado em Ensino do 1.º CEB e de Matemática e Ciências Naturais no 2.º CEB. Para além do enquadramento curricular realizado a nossa comunicação centra-se na intervenção concretizada numa turma do 1.º ano e numa outra do 3.º ano do Ensino Básico num contexto dos Observatórios Livres de Prática Pedagógica deste mestrado. A proposta de intervenção dos cenários de aprendizagem incidiu a utilização da tecnologia, concretamente, através o uso de beebots, ferramentas que permitem trabalhar, além de tópicos matemáticos, também a autonomia, o trabalho em equipa, a correção do erro, aprendizagem por tentativa e erro, etc. Este trabalho teve uma relevância particular por ter sido possível, com base numa ideia comum, planear para dois anos de escolaridade e refletir posteriormente sobre a importância dos materiais criados, das resoluções das crianças e dos diálogos estabelecidos na exploração de determinadas capacidades matemáticas, numa perspetiva individualizada e de grupo desenvolvidos em cada contexto educativo. Notas biográficas Jéssica Silva | João Tiago Dos Santos Gonçalves – Atualmente a frequentar o Mestrado em Ensino do 1.º CEB e de Matemática e Ciências Naturais no 2.º CEB da Escola Superior de Educação do Instituto Politécnico do Porto. Naturais da ilha da Madeira, vieram, neste ano letivo, para esta instituição para prosseguir o sonho de serem professoesr na especialidade de Matemática e Ciências Naturais. Um dos desafios pelos quais se depararam nesta nova aventura longe de casa foi a Unidade Curricular de Didática da Matemática do 1.º CEB em que, a docente responsável e que leciona esta disciplina propôs o desafio de aprofundar o estudo sobre as Capacidades Matemáticas das Aprendizagens Essenciais (2021), numa perspetiva curricular teórica e, simultaneamente, de criação e implementação de cenários concretos de aprendizagem matemática. |
[Início_SC]
SC 05 | B – A promoção da educação financeira por meio das aprendizagens essenciais: um olhar para a matemática no salárioReullyanne Freitas de Aguiar | Alexandra Sofia da Cunha Rodrigues | Francisco Alexandre de Lima Sales | Raimundo Luna Neres Terça-feira, 16 de julho, 11h30m - 12h30m Resumo Esta comunicação visa evidenciar o potencial das discussões e das aprendizagens da educação matemática em contextos que entrelacem a educação financeira, matemática financeira e os modelos matemáticos nas finanças dos salários. Em termos metodológicos, serão apresentados algumas tarefas e as articulações que os docentes podem realizar, utilizando os conhecimentos matemáticos, e que auxiliem para a cidadania e justiça social, ao utilizar a matemática em/para a ação. Conhecer objetivos que implicam as aprendizagens essenciais auxiliará professores de matemática a conseguir planejar um ensino em que o estudo do salário e o planejamento familiar seja mais eficaz. Dessa forma, a reflexão e discussão sobre os aspectos da educação financeira, durante as aulas, pode ser um ponto de partida para o incentivo a tomada de decisão nos alunos, contribuindo para um pensamento crítico e reflexivo. Notas biográficas Reullyanne Freitas de Aguiar – Doutoranda pelo Programa de Pós-Graduação em Educação em Ciências e Matemática (PPGECEM/REAMEC). Realiza o doutorado sanduíche na Universidade Nova de Lisboa. Líder do Grupo de Pesquisa em Laboratório de Educação Matemática (GEPLEMAT) e professora EBTT no Instituto Federal de Educação, Ciência e Tecnologia do Maranhão (IFMA), Campus: Buriticupu. Áreas de interesses para pesquisa: Educação Financeira, Educação Matemática e Formação de Professores de Matemática. Alexandra Sofia da Cunha Rodrigues – Doutora em Didática da Matemática pela Universidade da Beira Interior. Tem uma Especialização em Inovação e criatividade – as TIC e outra em Administração e Gestão Escolar. É professora da Faculdade de Ciências e Tecnologia da Universidade NOVA de Lisboa. Os interesses de investigação são diversificados, privilegiando a história da educação e o ensino e a aprendizagem da matemática no ensino profissional. Francisco Alexandre de Lima Sales – Doutorando pelo Programa de Pós-Graduação em Educação em Ciências e Matemática (PPGECEM/REAMEC). Realiza o doutorado sanduíche na Universidade Nova de Lisboa. Líder do Grupo de Pesquisa em Laboratório de Educação Matemática (GEPLEMAT) e professor EBTT no Instituto Federal de Educação, Ciência e Tecnologia do Maranhão (IFMA), Campus: Buriticupu. Áreas de interesses para pesquisa: Análise quantitavo de dados textuais, pesquisa como príncipio educativo, Educação Matemática e Formação de Professores de Matemática. Raimundo Luna Neres – Doutor em Educação pela Universidade Estadual Paulista Júlio de Mesquita Filho - UNESP/SP. Professor da Universidade CEUMA. Docente do Programa de Pós-Graduação Doutorado em Educação em Ciências e Matemática - REAMEC. Professor do Programa de Pós-Graduação em Gestão de Ensino da Educação Básica - UFMA. Líder do Grupo de Pesquisa: Educação Matemática, Ciências e Produção de Saberes. Pesquisa na área de Educação Matemática com ênfase em Registros de Representação Semiótica, Ensino e Aprendizagem da Matemática e Formação Continuada de Professores de Matemática. |
[Início_SC]
SC 05 | C – Interlocução Coletiva na construção das Aprendizagens Essenciais de MatemáticaHelena Gil Guerreiro | Susana Brito Terça-feira, 16 de julho, 11h30m - 12h30m Resumo O ano letivo que agora termina foi o ano da generalização do novo programa de matemática para todos os anos do 1.º CEB. Este programa traz um alargamento das aprendizagens definidas como essenciais. Aprendizagens matemáticas que envolvem conhecimentos, mas também capacidades matemáticas. Envolvem pensar a natureza das tarefas que se escolhem, desenvolver uma abordagem exploratória na aula de matemática e, sobretudo, a aceitação de uma nova cultura de sala de aula, como destaca Leonor Santos, coordenadora do grupo de Trabalho do Desenvolvimento Curricular e Profissional em Matemática. É nesta perspetiva que vimos partilhar momentos da exploração de tarefas numa turma da operacionalização antecipada do 4.º ano, desenvolvidas no ano letivo de 2022/2023. Trazemos um foco na discussão coletiva de tarefas. Evidenciamos a interlocução coletiva na construção conjunta de aprendizagens e os registos escritos para memória da turma. Notas biográficas Helena Gil Guerreiro – Professora no 1.º Ciclo no Agrupamento de Escolas Braamcamp Freire e professora adjunta convidada na Escola Superior de Educação de Lisboa. No ano letivo 2022/2023 integrou o grupo de Trabalho do Desenvolvimento Curricular e Profissional em Matemática. Doutorada em Educação, na área de especialidade de Didática da Matemática pelo Instituto de Educação da Universidade de Lisboa, mestre na área de especialidade da Didática da Matemática, pela Faculdade de Ciências, da Universidade de Lisboa e Escola Superior de Educação do Instituto Politécnico de Lisboa e licenciada em Ensino Básico, variante Matemática/Ciências da Natureza pela Escola Superior de Educação do Instituto Politécnico de Lisboa. Susana Brito – Professora no 1.º Ciclo e representante da área de matemática no Agrupamento de Escolas Braamcamp Freire. No ano letivo 2022/2023 foi professora operacionalizadora das Novas Aprendizagens Essenciais de Matemática do 4.º ano. Bacharel em ensino do 1.º Ciclo do Ensino Básico pela Escola Superior de Educação João de Deus, licenciada no Ensino Básico variante Matemática/Ciências da Natureza pela Escola Superior de Educação Almeida Garret e pós-graduação em Didática da Matemática, pela Faculdade de Ciências, da Universidade de Lisboa e Escola Superior de Educação do Instituto Politécnico de Lisboa. |
[Início_SC]
SC 06 – Math City Map – Trilhos matemáticos nas Caldas da RainhaDora Vaz Pinto, Escola Secundária Raul Proença Terça-feira, 16 de julho, 15h00m - 16h00m Resumo Um “trilho matemático” é um percurso fora da sala de aula em que é necessário passar por determinados locais e resolver tarefas. Usando a aplicação Math City Map no telemóvel, o utilizador dirige-se a um local indicado num mapa onde é desafiado com uma questão que pode envolver observações, medições, cálculos, etc. Quando responde corretamente, aparece o local seguinte no mapa, com uma nova tarefa. No início deste ano letivo, a APM convidou os professores de matemática dos três agrupamentos de escolas das Caldas da Rainha para participarem no projeto “Math City Map nas Caldas da Rainha” com o objetivo de criar trilhos matemáticos que permitiriam explorar a cidade em julho, durante o ProfMat 2024. Este trabalho envolveu mais de 500 alunos, desde o 2.º Ciclo do Ensino Básico ao Ensino Secundário, e promoveu as ideias-chave das novas aprendizagens de matemática. Nesta comunicação, pretende-se partilhar esta experiência com os docentes interessados nesta temática. Serão apresentados exemplos de tarefas criadas pelos alunos das Caldas da Rainha para os trilhos “APM – Matemática para todos”, “APM – 3.º Ciclo” e “APM – Secundário”. Notas biográficas Dora Vaz Pinto – Licenciada em Matemática (Ramo de Formação Educacional), pela Universidade do Algarve e Pós-Graduada em Matemática Aplicada, pela Universidade Lusíada. Docente de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário, desde 2004, atualmente no Agrupamento de Escolas Raul Proença (Caldas da Rainha). Joana Domingos – Licenciada em Ensino, do Curso de Professor do Ensino Básico variante Matemática e Ciências da Natureza, na Escola Superior de Educação de Leiria, do Instituto Politécnico de Leiria. Docente desde 1997. Professora do QA da Escola EB D. João II, Caldas da Rainha, desde 2018. Coordenadora de Sub-Departamento de Matemática e Tecnologias informação e Comunicação desde 2021. Manuel João Marques – Licenciado em Matemática Ramo Educacional, pela Faculdade de Ciências da Universidade de Coimbra. Docente de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário, desde 2001, atualmente na Escola Secundária Afonso Lopes Vieira (Leiria). Coautor de manuais escolares do 3.º Ciclo, entre 2001 e 2012. Formador acreditado pelo Conselho Científico-Pedagógico da Formação Contínua, desde 2013. Atualmente, exerce funções na Associação de Professores de Matemática (APM) e é coordenador do Grupo de Trabalho CASIO+ da APM. Pedro Mesquita Santos – Licenciado em Matemática (Ramo de Formação Educacional) pela Faculdade de Ciências e Tecnologia da Universidade de Coimbra. Docente de Matemática do 3.º Ciclo do Ensino Básico e do Ensino Secundário, desde 1994. Professor na escola Secundária Rafael Bordalo Pinheiro (ESRBP), desde 1997. Coordenador dos cursos de Educação e Formação de Adultos (EFA). |
[Início_SC]
SC 07 | A – A Modelação como estratégia de ensino da MatemáticaAna Lopes | Alexandra Rodrigues Terça-feira, 16 de julho, 11h30m - 12h30m Resumo Esta comunicação visa evidenciar o potencial da utilização da modelação no ensino da matemática, partindo da investigação realizada no estágio e que teve como objetivo: compreender o papel da modelação para a aprendizagem da proporcionalidade. Atualmente existe um reconhecimento da importância da modelação matemática e introdução de tarefas exploratórias no desenvolvimento das capacidades dos alunos e na promoção das aprendizagens, no entanto, ainda se mantêm algumas preocupações por parte dos professores, quer relativas à construção e condução das atividades, quer no acompanhamento dos próprios alunos. Ao partilhar a experiência vivenciada decorrente da implementação de uma tarefa com recurso à modelação descrevendo os procedimentos adotados, os desafios enfrentados e os aspetos positivos identificados, acredita-se ser possível desmitificar e incentivar a modelação matemática como estratégia de ensino. Notas biográficas Ana Lopes – Frequenta o Mestrado em Ensino da Matemática no 3.º Ciclo do Ensino Básico e no Ensino Secundário na Faculdade de Ciências e Tecnologias, Universidade NOVA de Lisboa. Alexandra Rodrigues – Doutora em Didática da Matemática pela Universidade da Beira Interior. Tem uma Especialização em Inovação e criatividade – as TIC e outra em Administração e Gestão Escolar. É professora da Faculdade de Ciências e Tecnologia da Universidade NOVA de Lisboa. Os interesses de investigação são diversificados, privilegiando a história da educação e o ensino e a aprendizagem da matemática no ensino profissional. |
[Início_SC]
SC 07 | B – Centro de estudos em História da Matemática e Educação CientíficaTeresa Costa Clain, GHMEM do CIDMA/Universidade de Aveiro Terça-feira, 16 de julho, 11h30m - 12h30m Resumo Este projeto centra-se na formação dos docentes de Matemática, no sentido de os “conquistar” para o uso da História da Matemática (HM) na sala de aula. Propomos a dinamização de sessões de formação/divulgação e de formação contínua acreditada, presencialmente e a distância. Nestes momentos de formação os docentes deverão encontrar respostas que contrariem as objeções usualmente levantadas como a “falta de conhecimento” e “falta de tempo”. Entre os pares, serão criados materiais para a prática letiva e com partilha de práticas. Pretendemos criar de uma página web com recursos diversos: materiais para uso em contexto escolar (informação e problemas) de HM enquadrados nos conteúdos programáticos em todos os ciclos de ensino. Nota biográfica Teresa Costa Clain – Docente de Matemática no Agrupamento de Escolas Coimbra Centro, é formadora e colaboradora do Grupo de História da Matemática e Educação Matemática do CIDMA da Universidade de Aveiro (UA), onde desenvolve investigação sobre a História da Matemática e as suas aplicações na sala de aula. Participa no Projeto “Histórias com Ciência na Biblioteca Escolar”, da UA e da Rede Nacional de Bibliotecas Escolares. É membro da Comissão Consultiva do HPM (International Study Group on the Relations Between the History and Pedagogy of Mathematics), desde 2020. |
[Início_SC]
SC 07 | C – O que pensam alunos do ensino básico sobre os trabalhos para casaCristina Fernandes | Manuel Vara Pires Terça-feira, 16 de julho, 11h30m - 12h30m Resumo Esta comunicação pretende apresentar e discutir ideias de alunos do 2.º ciclo do ensino básico sobre os trabalhos de casa (TPC) recolhidas num estudo desenvolvido no âmbito da prática de ensino supervisionada (PES) concretizada num mestrado profissionalizante para a docência. Os TPC, assumidos como tema integrador da PES, registam um grande presença e utilização no processo de ensino e aprendizagem desde há longo tempo, embora mantendo sempre controvérsias e divergências de opinião dos diversos atores envolvidos. Neste sentido, uma das dimensões do estudo orientou-se para a análise das ideias reveladas pelos alunos relativamente ao trabalho que realizam fora da sala de aula. Os dados foram recolhidos através de um questionário e analisados com recurso à análise de conteúdo. Globalmente, os alunos participantes reconhecem que os TPC são (muito) importantes no processo de ensino e aprendizagem, permitindo-lhes consolidar os conhecimentos, melhorar as aprendizagens, desenvolver a autonomia, incentivar o estudo e promover métodos de trabalho, embora possam condicionar a gestão dos seus tempos fora da escola. Notas biográficas Cristina Fernandes – Professora do 1.º CEB e de Matemática e Ciências Naturais no 2.º CEB, recentemente diplomada pela Escola Superior de Educação do Instituto Politécnico de Bragança. A educação básica, em especial a educação matemática e a educação científica, corresponde à sua principal área de interesse profissional e de estudo. Manuel Vara Pires – Professor no Departamento de Matemática da Escola Superior de Educação do Instituto Politécnico de Bragança e membro integrado do Centro de Investigação em Educação Básica. A educação matemática, a formação e desenvolvimento profissional de professores e a educação básica constituem as suas principais áreas de interesse profissional e de investigação. |
[Início_SC]
SC 08 | A – Uma visão da Matemática no currículo das Escolas EuropeiasPaula Gomes, Escola Europeia de Bruxelas II/Escola Secundária de Vila Verde Terça-feira, 16 de julho, 15h00m - 16h00m Resumo Todos os professores têm uma opinião acerca do que deve integrar o currículo da disciplina de Matemática nos diversos níveis de ensino: quais os temas que devem ser abordados; em que nível devem ser ensinados; qual o grau de profundidade; por que ordem devem ser ensinados; entre outros aspetos. As Escolas Europeias têm dois objetivos fundamentais: proporcionar uma educação formal (que envolve a aquisição de oito competências) e incentivar o desenvolvimento pessoal dos alunos num contexto social e cultural mais amplo. Para concretizar estes dois objetivos, os programas das diversas disciplinas foram atualizados nos últimos cinco anos, nomeadamente, o programa da disciplina de Matemática. Nesta comunicação serão apresentados os objetivos gerais, os princípios didáticos, os objetivos de aprendizagem, as competências, os conceitos transversais e os tópicos, que integram o currículo da disciplina de Matemática nas Escolas Europeias (www.eursc.eu/en). Nota biográfica Paula Gomes – É licenciada e concluiu o Mestrado em Ensino de Matemática pela Universidade do Minho, em 2006. Exerce funções docentes, em regime de mobilidade estatutária, na Escola Europeia de Bruxelas II e pertence ao quadro da Escola Secundária de Vila Verde. Pertence ao núcleo da APM de Braga e pertenceu à direção da APM. Os seus principais interesses prendem-se com a utilização da tecnologia no ensino da Matemática, nomeadamente a calculadora gráfica. |
[Início_SC]
SC 08 | B – ContinueUP - conectando a formação inicial e a formação contínua de professoresJosé Miguel Sousa, Secretaria Regional da Educação, Ciência e Tecnologia – Madeira Terça-feira, 16 de julho, 15h00m - 16h00m Resumo O programa Erasmus (2021–2027) introduz uma nova ação, Erasmus+ Teacher Academies, que visa criar parcerias europeias e promover a cooperação entre instituições superiores de formação de professores e entidades no âmbito da formação contínua de professores. São financiados projetos que visam melhorar o apoio aos professores nos primeiros anos de profissão e reforçar o desenvolvimento profissional contínuo ao longo das suas carreiras. É o caso do projeto “ContinueUP - Co-constructing the continuum between initial teacher education and continuous professional development”, iniciado em setembro de 2023, com a duração de 3 anos, em que a Secretaria Regional de Educação, Ciência e Tecnologia é um dos principais parceiros. A coordenação deste projeto é da responsabilidade da European Schoolnet (EUN). É sobre este tipo de projetos, em particular dos produtos do ContinueUP que vamos falar nesta comunicação. Nota biográfica José Miguel Sousa – Licenciado em Matemática, Mestre em Matemática, com especialização em Administração Escolar e Administração Educacional. Entre 1995 e 2022 foi diretor do CFAE EduFor. Mentor e coordenador de vários projetos, onde se destaca “Managing for @ School of Success”, distinguido como pela Comissão Europeia. É orador em eventos, onde se destaca “Tablets em Sala de Aula: um caminho possível”. Atualmente ocupa o cargo de Diretor-Geral da DTIM – Associação Regional para o Desenvolvimento das Tecnologias de Informação na Madeira e representa a Secretaria Regional de Educação, Ciência e Tecnologia no projeto ContinueUP. |
[Início_SC]
SC 09 | A – Laboratório de Matemática - passagem do 1.º para 2.º ciclo - Dia do AgrupamentoVirgínia Fernanda das Neves Ferreira | Agrupamento de Escolas António Nobre, Porto Quarta-feira, 17 de julho, 9h00m - 10h00m Resumo A base desta comunicação fundamenta-se em destacar a importância do ensino da Matemática através do lúdico e das experiências vividas pelos alunos, numa passagem do Primeiro para o Segundo ciclo do Ensino Básico. A Matemática é fundamental nas nossas vidas e é de extrema importância trabalhá-la desde cedo, de forma divertida e apelativa. As atividades desenvolvidas no Laboratório de Matemática realizadas no dia do Agrupamento, tiveram por base, situações do quotidiano dos alunos, nomeadamente, o Estimar, um desafio Matemático e um Cálculo Mental. Refletindo assim sobre as situações trabalhadas e desenvolvidas no Laboratório, é de extrema importância que o professor deva estar preparado e “abusar” da sua criatividade proporcionando prazer em ensinar os alunos para que o resultado seja positivo. Concluiu-se que pelo facto dos alunos terem vivido estas experiências de forma diferenciadora, estas traduziram-se num fator facilitador das aprendizagens em sala de aula. Nota biográfica Virgínia Fernanda das Neves Ferreira – Mestrado em Supervisão Pedagógica – Universidade do Minho. Leciona no Agrupamento de Escolas António Nobre, no Porto. |
[Início_SC]
SC 09 | B – Problema de Fermi no âmbito do projeto de Flexibilidade Curricular no 8.º ano de escolaridadeManuela Subtil | Agrupamento de Escolas Fragata do Tejo / Escola Superior de Educação de Lisboa Quarta-feira, 17 de julho, 9h00m - 10h00m Resumo Os alunos do 8.º ano de escolaridade, em grupo, resolveram um problema de Fermi, no âmbito do Projeto de Flexibilidade Curricular, cujo tema foi a Interculturalidade. Os alunos foram desafiados a escolher um espaço de grandes dimensões, situado no Brasil ou na Roménia. Aí deveriam colocar WCs, barracas de bebida e comida, um palco e realizarem uma estimativa de quantas pessoas é possível lá colocar para assistir a um concerto de um grupo musical da sua preferência. Utilizando uma metodologia de investigação qualitativa de natureza interpretativa e descritiva, adotou-se a modalidade estudo de caso, os grupos. Os métodos utilizados para recolher os dados focaram-se em registos fotográficos, registos escritos dos alunos e diário de bordo. Através da monitorização da professora, os alunos conseguiram realizar estimativas de quantas pessoas poderiam assistir ao concerto, no espaço que escolheram. Foram desenvolvidos vários conteúdos de aprendizagem de acordo com as Novas Aprendizagens Essenciais da Matemática. Nota biográfica Manuela Subtil – Professora de Matemática do grupo 500 e professora adjunta convidada do domínio científico de Matemática. É Licenciada e Mestre em Ensino de Matemática no 3.º Ciclo e Ensino Secundário e Doutora em Ciências da Educação. É autora de livros escolares e artigos publicados em revistas. Também tem publicados, posters e comunicações, em atas de congressos nacionais e internacionais. É investigadora colaboradora do CICS.NOVA e UIED. |
Exposições
ÂNGULOS DAS CALDAS
Autor: Manuel Bandeira Duarte
Local da Exposição: Centro Cultural e de Congressos
"Esta exposição surge a propósito do convite que me foi endereçado para compor a Capa e a Contracapa da Agenda “Dia-a-dia com a Matemática”, 2024/25. Assim, aceitando o convite, pretendi enaltecer uma das características da cidade onde decorre, neste momento, o “XXXIX ProfMap”, ou seja, as Caldas da Rainha. Como forma de eternizar este evento, a Agenda conta com uma ilustração de um dos ex-líbris desta Cidade e deste Município. Convido-o, agora, a conhecer um pouco de cada um dos ângulos que constituem o território concelhio de Caldas da Rainha."

Nota biográfica
Natural de Caldas da Rainha, Manuel Bandeira Duarte é Creative Designer e, desde cedo, que se envolve em distintas vertentes artísticas, sendo já várias as suas abordagens profissionais em torno das Caldas da Rainha. Habitualmente, para além dos trabalhos artísticos e gráficos, o autor estende o seu leque de intervenções aos espaços cénicos e habitacionais, bem como ao domínio das Artes Plásticas. Tem, ainda, trabalhado ativamente nas áreas do associativismo e da defesa ambiental.
RECORDAR HENRIQUE GUIMARÃES
(1951 - 2022)
Local da Exposição: ESRBP, Bloco 2, Piso 2 (Corredor das Sessões Práticas)
E unicamente ao movimento de crescer nos guiasse. Termos das árvores
A incomparável paciência de procurar o alto
A verde bondade de permanecer
E orientar os pássaros
(Daniel Faria, in Explicação das árvores e de outros animais, 1998)
Esta é uma presença outra do Henrique entre nós, habituados que estávamos a vê-lo, a conversar com ele, a assistir às suas conferências nos ProfMats que ele seguiu na totalidade, inscrevendo-se e participando sempre.
RECORDAR EDUARDO VELOSO
(1928 - 2022)
Local da Exposição: ESRBP, Bloco 2, Piso 2 (Corredor das Sessões Práticas)
Recordar o Eduardo Veloso é uma exposição que revisita algumas ideias significativas daquele que foi um dos sócios fundadores da APM, grande entusiasta e animador de muitas das atividades associativas.
Esta exposição, cuja ideia partiu de uma proposta da direção da APM, foi pensada pelos seus organizadores como uma oportunidade de expor algumas das principais ideias do Eduardo Veloso sobre a APM, a Educação em geral e o Ensino da Matemática, ideias que defendia consistentemente, sempre numa base de grande coerência, e que partilhava muitas vezes informalmente numa primeira fase para depois passar a escrito e divulgar ou defender em fóruns diversos.
ProfMat 2024 - Sessões Especiais (60 min)
Moderador: José Miguel Sousa
|
SE 01 |
Agenda APM 2024/2025 "Dia-a-dia com a Matemática" (Resumo) António Fernandes |
Terça-feira, 16 de julho 17h30 - 18h30 |
Grande Auditório do CCC |
| SE 02 |
Educação e Matemática - Materiais para a Aula de Matemática (Resumo) A equipa da revista |
Terça-feira, 16 de julho 17h30 - 18h30 |
Grande Auditório do CCC |
| SE 03 |
Niu Aleph B10 (Resumo) Jaime Carvalho e Silva |
Terça-feira, 16 de julho 17h30 - 18h30 |
Grande Auditório do CCC |
| SE 04 |
Com Pólya, Vamos Resolver Problemas... e com Henrique Guimarães (Resumo) António Fernandes |
Terça-feira, 16 de julho 17h30 - 18h30 |
Grande Auditório do CCC |
SE 01 – Agenda APM 2024/2025 "Dia-a-dia com a Matemática"António Fernandes | Manuel João Marques | Manuel Bandeira Duarte | Vera Marques Terça-feira, 16 de julho, 17h30m - 18h30m Resumo A edição 2024/2025 da Agenda "Dia-a-dia com a Matemática" foi elaborada pela APM, em parceria com a Câmara Municipal das Caldas da Rainha, com o objetivo de promover o patrimómio cultural e artístico desta Cidade Criativa da UNESCO, bem como de divulgar alguns trabalhos realizados pelos alunos dos A. E. Dom João II, Rafael Bordalo Pinheiro e Raul Proença, no âmbito de duas iniciativas dinamizadas pela APM com docentes de Matemática: o concurso “Cartaz do ProfMat e do SIEM 2024” e o projeto “Math City Map nas Caldas da Rainha”. |
SE 02 – Educação e Matemática - Materiais para a Aula de MatemáticaA equipa da revista Terça-feira, 16 de julho, 17h30m - 18h30m Resumo A Educação e Matemática é a materialização das nossas ações em sala de aula, da nossa prática, das nossas reflexões. É também um espaço onde recorremos para nos inspirarmos no trabalho de todos e usarmos os recursos que estão disponíveis a cada publicação. A existência da secção Materiais para a Aula de Matemática é um testemunho disso. Uma secção que, com tanta história, revela-se uma referência em tarefas e que com o passar dos anos faz com que contemos com um vasto leque de recursos para os diversos anos letivos e temas. Estes recursos foram agora organizados e estarão disponíveis num catálogo online, no site da APM, que vos convidamos a vir conhecer, nesta sessão de fim de tarde. |
SE 03 – Niu Aleph B10Jaime Carvalho e Silva | Joaquim Pinto Terça-feira, 16 de julho, 17h30m - 18h30m Resumo Cada vez mais, a Matemática é importante no século XXI. Cada vez mais, são maiores as exigências do mundo moderno, obrigando a lidar com questões complexas e variadas. As novas Aprendizagens Essenciais da disciplina de Matemática B (Matemática Aplicada às Artes Visuais) pretendem responder a esta exigência. Se olharmos à nossa volta, observamos muitas manifestações da Matemática, nomeadamente da Geometria. A Geometria é referida nas novas Aprendizagens Essenciais da disciplina de Matemática B (Matemática Aplicada às Artes Visuais) como estando “de tal modo presente na natureza, que a Arte frequentemente se sustenta na Geometria para a descrever”. As novas Aprendizagens Essenciais pretendem ir “ao encontro das motivações e interesses dos alunos e também do perfil dos alunos dos Cursos de Artes Visuais”. Este livro em linha, gratuito e permanentemente atualizado, oferece aos estudantes e aos professores materiais para as Aprendizagens Essenciais da disciplina de Matemática B (Matemática Aplicada às Artes Visuais) de acordo com os temas que constam dos documentos oficiais. Coordenação: Jaime Carvalho e Silva |
SE 04 – Com Pólya, Vamos Resolver Problemas... e com Henrique GuimarãesAntónio Fernandes | Lurdes Figueiral Terça-feira, 16 de julho, 17h30m - 18h30m Resumo Sessão de lançamento e apresentação do livro póstumo de Henrique Manuel Guimarães, Com Pólya, Vamos Resolver Problemas. Henrique Guimarães foi sempre um convicto defensor da Resolução de Problemas no trabalho matemático. No seu ensino e na sua aprendizagem, também. Fascinava-o a exploração de um bom problema e pôde partilhá-lo com os seus alunos e com os professores de Matemática que o ouviram em tantas conferências e encontros. Este livro é o seu último trabalho sobre Resolução de Problemas e George Pólya. |
XXXIV SIEM — Apresentação
O SIEM – Seminário de Investigação em Educação Matemática, nasceu dada a necessidade sentida por quem se interessa pela investigação em educação matemática de conhecer e discutir os novos desenvolvimentos na área, os trabalhos em curso, e as suas implicações para a prática profissional, a formação de professores e a política educativa. Desde sempre, os participantes têm sido não só investigadores nacionais e internacionais, mas também professores dos diferentes níveis de ensino, muitos dos quais envolvidos em cursos de pós-graduação. Procurando valorizar a investigação, o SIEM, que tem uma parte do seu programa comum com o ProfMat, mantém uma forte preocupação em aprofundar a sua ligação com os interesses e necessidades dos professores, contribuindo assim para a melhoria das aprendizagens matemáticas dos alunos.
34 anos depois, o SIEM regressa às Caldas da Rainha!
Comissões — SIEM
COMISSÃO ORGANIZADORA - XXXIV SIEM
Ana Oliveira
Dina Tavares
Hélia Pinto
Hugo Menino
João Pedro da Ponte
Joaquim Pinto
Lurdes Serrazina
Manuel João Marques
Marina Rodrigues
Nadia Ferreira
Nicole Duarte
Nuno Rainho
Pedro Mesquita
Raquel Vieira
Rita Cadima
Rogério Costa
Soraia Farinha
COMISSÃO CIENTÍFICA - XXXIV SIEM
Alexandra Gomes, CIEC, Universidade do Minho, Portugal
Ana Barbosa, inED, Instituto Politécnico de Viana do Castelo, Portugal
Ana Caseiro, CIED, Instituto Politécnico de Lisboa, Portugal
Ana Elisa Esteves Santiago, NIEFI, CICS.NOVA, Instituto Politécnico de Coimbra, Portugal
Ana Isabel Silvestre, CI&DEI, Instituto Politécnico de Leiria, Portugal
Ana Oliveira, CI&DEI, Instituto Politécnico de Leiria, Portugal
Ana Paula Canavarro,Universidade de Évora, Portugal
António Domingos, CICS.NOVA, FCT, Universidade NOVA de Lisboa, Portugal
António Guerreiro, Universidade do Algarve, Portugal
Berta Barquero, Universitat de Barcelona. Departamento de Educación Lingüística, Científica y Matemática, Espanha
Carlos Miguel Ribeiro, CIEspMat, Faculdade de Educação da UNICAMP, Brasil
Catarina Delgado, CIEF/IPS, Instituto Politécnico de Setúbal, Portugal
Célia Mestre, Instituto Politécnico de Setúbal, Portugal
Cláudia Torres, AE D. Dinis Lisboa, Projeto #EstudoEmCasa Apoia, Ministério da Educação, Ciência e Inovação, Portugal
Cristina Martins, CIEB, Instituto Politécnico de Bragança, Portugal
Dina Tavares, CI&DEI, Instituto Politécnico de Leiria, Portugal
Ema Mamede, CIEC, IE, Universidade do Minho, Portugal
Fátima Fernandes, inED, Instituto Politécnico de Viana do Castelo, Portugal
Fátima Regina Jorge, Instituto Politécnico de Castelo Branco, Portugal
Fátima Mendes, CIEF/IPS, Instituto Politécnico de Setúbal, Portugal
Fernando Martins, NIEFI, UNICID, iiA, RoboCorp, inED, ESEC, Instituto Politécnico de Coimbra, Portugal
Graça Cebola, Instituto Politécnico de Portalegre, Portugal
Helena Martinho, CIEd-UM, Universidade do Minho, Portugal
Helena Rocha, CICS.NOVA, Faculdade de Ciências e Tecnologia, Universidade NOVA de Lisboa, Portugal
Hélia Jacinto, UIDEF, IE, Universidade de Lisboa, Portugal
Hélia Oliveira, UIDEF, IE, Universidade de Lisboa, Portugal
Hélia Pinto, CI&DEI, Instituto Politécnico de Leiria, Portugal
Hugo Menino, CI&DEI, Instituto Politécnico de Leiria, Portugal
Isabel Cabrita, Universidade de Aveiro, Portugal
Isabel Vale, CIEC-UM, Instituto Politécnico de Viana do Castelo, Portugal
João Pedro Ponte, UIDEF, IE, Universidade de Lisboa, Portugal
Joaquim Pinto, Departamento de Educação e Psicologia da Universidade de Aveiro, Portugal
Jorge Henrique Gualandi, Instituto Federal do Espírito Santo - campus Cachoeiro de Itapemirim, Brasil
Leonor Santos, UIDEF, IE, Universidade de Lisboa, Portugal
Lina Fonseca, CIEC-UM, Instituto Politécnico de Viana do Castelo, Portugal
Lurdes Serrazina, UIDEF, IE, Instituto Politécnico de Lisboa, Portugal
Manuel Vara Pires, CIEB, Instituto Politécnico de Bragança, Portugal
Margarida Rodrigues, UIDEF, IE, Instituto Politécnico de Lisboa, Portugal
Maria Cristina Costa, Smart Cities Research Center, Instituto Politécnico de Tomar, Portugal
Maria de Fátima Mendes, CIEQV, ESE, Instituto Politécnico de Setúbal
Maria Teresa Fernandez Blanco, Open STEAM, Universidade de Santiago de Compostela, Espanha
Marina Rodrigues, CI&DEI, Instituto Politécnico de Leiria, Portugal
Marisa Quaresma, UIDEF, IE, Universidade de Lisboa, Portugal
Nádia Ferreira, CIE, ISPA - Instituto Universitário, Portugal
Nélia Amado, UIDEF, IE, Faculdade de Ciências e Tecnologia, Universidade do Algarve, Portugal
Neusa Branco, ESSE, Instituto Politécnico de Santarém, Portugal
Nicole Duarte, CI&DEI, Instituto Politécnico de Leiria, Portugal
Paula Teixeira, Agrupamento de Escolas João de Barros, Portugal
Paulo Afonso, CIPEC, Instituto Politécnico de Castelo Branco, Portugal
Pedro Palhares, Universidade do Minho, Portugal
Pedro Tadeu, CI&DEI - Escola Superior de Educação, Comunicação e Desporto - Instituto Politécnico da Guarda, Portugal
Raquel Santos, CIEQV, Instituto Politécnico de Santarém, Portugal
Rita Cadima, CI&DEI, Instituto Politécnico de Leiria, Portugal
Rosa Ferreira, CMUP, Universidade do Porto, Portugal
Susana Colaço, ESE, Instituto Politécnico de Santarém, Portugal
Teresa Neto, CIDTFF, Universidade de Aveiro, Portugal
Locais do SIEM
O XXXIV SIEM decorre nas Caldas da Rainha, mais especificamente em dois locais:
CENTRO CULTURAL E CONGRESSOS DE CALDAS DA RAINHA (CCC)
Mapa:
Rua Dr. Leonel Sotto Mayor 23D, 2500-227 Caldas da Rainha
Tlf: 262 094 081
Email: bilheteira@ccc.com.pt
URL: https://ccc.com.pt
 |
 |
 |
 |
ESCOLA SECUNDÁRIA RAFAEL BORDALO PINHEIRO (ESRBP)
Mapa:
Rua Almirante Gago Coutinho 1, 2500-000 Caldas da Rainha
Tlf: 262 870 070
Email: esrbp@esrbp.pt
URL: https://aerbp.pt
 |
 |
 |
 |
MAPA DA ZONA ENVOLVENTE
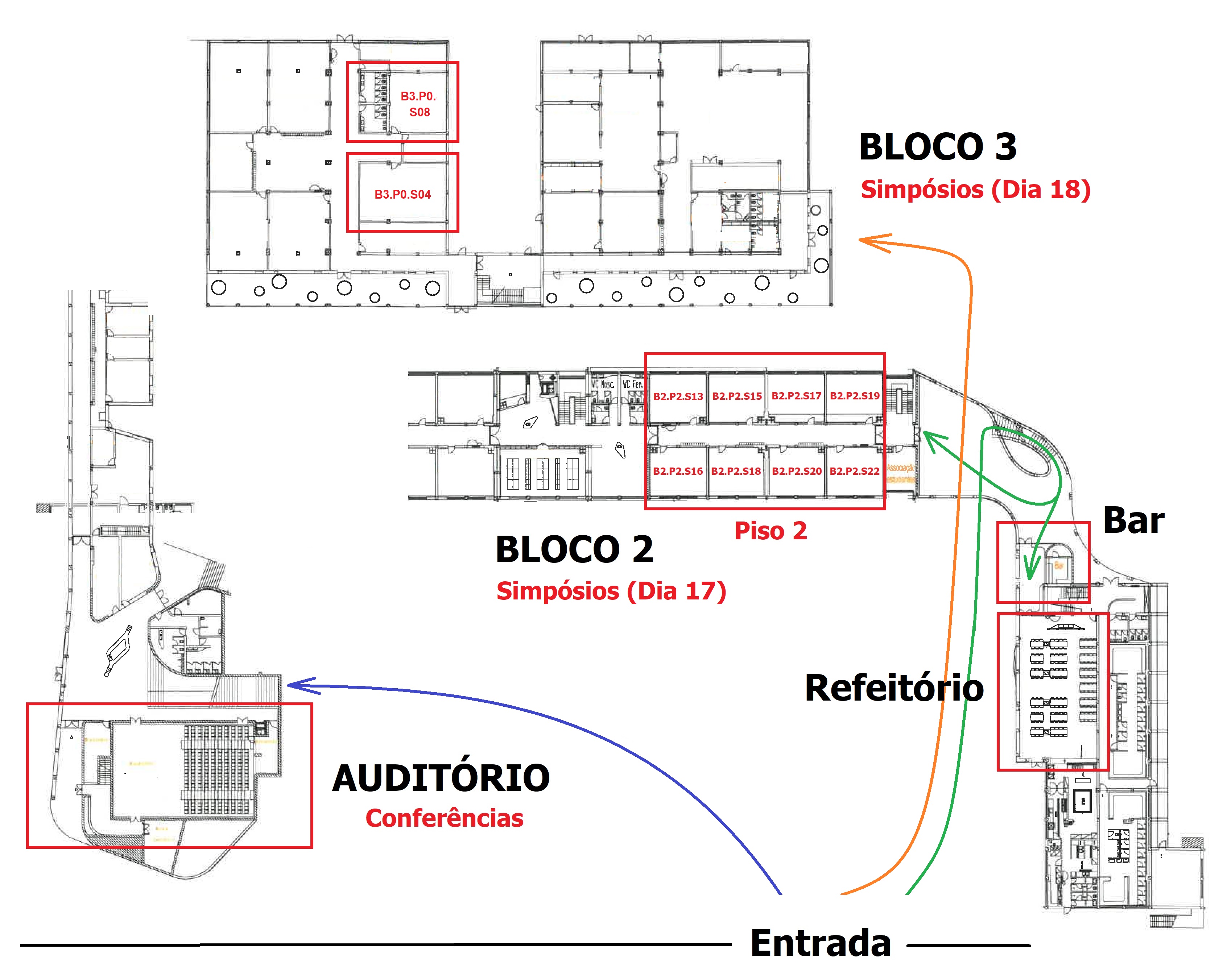
MAPA DA E. S. RAFAEL BORDALO PINHEIRO
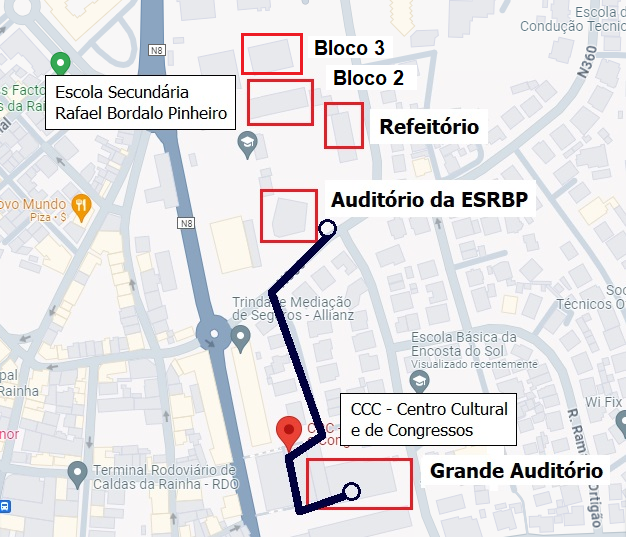
Programa — SIEM

Submissão de Comunicações e Pósteres
Os participantes no SIEM podem submeter propostas de comunicações e/ou pósteres, a serem apresentadas em simpósios com discussão. As comunicações têm 15 minutos para apresentação e os pósteres têm 5 minutos para apresentação. Todos os trabalhos serão sujeitos a revisão científica por pares, com base em critérios uniformes indicados pela comissão científica relativos a clareza, estrutura, relevância e coerência da proposta. As propostas devem seguir rigorosamente as indicações formais abaixo fornecidas e serem enviadas até 19 de maio, através dos formulários abaixo.
A notificação de aceitação é realizada pela comissão científica até 31 de maio e a submissão da versão final revista para publicação em atas tem de ser enviada até 17 de junho.
As atas do XXXIV SIEM irão ser propostas para indexação na Web of Science.
COMUNICAÇÕES
O texto da comunicação será publicado nas Atas se respeitar rigorosamente as normas de formatação que constam no modelo.
Modelo para submissão de Comunicação
| Submissão de Comunicação |
PÓSTERES
O texto do póster será publicado nas Atas se respeitar rigorosamente as normas de formatação que constam no modelo.
Modelo para submissão de Póster
| Submissão de Póster |
Modelo de PowerPoint
Se vai apresentar alguma comunicação e/ou póster e pretende utilizar um modelo comum, próprio deste SIEM, descarregue-o aqui:
Almoço | Jantar do SIEM
Almoço - 17 de julho
Durante o SIEM2024, na quarta-feira, terá a possibilidade de almoçar no refeitório da E. S. Rafael Bordalo Pinheiro (pão, sopa, prato, salada, sobremesa e bebida). A inscrição no almoço e a respetiva escolha do prato (carne, peixe ou vegetariano) realiza-se através do formulário de inscrição no SIEM 2024.
O almoço tem um custo de 8 euros, pago no ato de inscrição.
QUARTA-FEIRA, 17 DE JULHO
| Sopa | Caldo verde |
| Prato de Carne | Carne de porco assada com massa esparguete e legumes salteados |
| Prato de Peixe | Salada russa de salmão |
| Prato Vegetariano | Rolinhos salsicha de tofu com lombardo com puré de batata |
| Sobremesa | Pudim de ovos ou fruta da época |
Jantar do SIEM 2024 - Quarta-feira 17 de julho, às 20:00
Após um passeio livre na Vila de Óbidos:
RESTAURANTE "ANTONIUS - in JOSEFA D'ÓBIDOS HOTEL"
Mapa:
Rua Dom João de Ornelas, 2510-074 Óbidos
Tlf: 262 955010 | 927214712
URL: https://josefadobidoshotel.com/
 |
 |
 |
 |
 |
 |
XXXIV SIEM — Atas
A disponibilizar no início de julho.
As atas do XXXIV SIEM irão ser propostas para indexação na Web of Science.
Contactos
siem2024@apm.pt
XXXIV SIEM - Associação de Professores de Matemática
Rua Dr. João Couto, n.º 27-A
1500-236 Lisboa
Tel.: +351 21 716 36 90 / 21 711 03 77
 |
 |
 |
 |
XXXIV SIEM - Conferências Plenárias (1h)
CP 01 – A discussão coletiva na aula exploratória de MatemáticaNicole Duarte, Escola Superior de Educação e Ciências Sociais do Instituto Politécnico de Leiria, CI&DEI Moderadora: Lurdes Serrazina, UIDEF, IE, Instituto Politécnico de Lisboa Quarta-feira, 17 de julho, 14h00m - 15h00m Resumo A discussão matemática coletiva é um aspeto fundamental da abordagem de ensino exploratório, em que os alunos assumem um papel central e ativo na construção do seu conhecimento. Apesar do potencial da discussão coletiva, esta apresenta desafios para o professor, dado o amplo conhecimento de que necessita para o gerir. O estudo de aula tem vindo a ser apontado como um processo formativo com potencial para promover o desenvolvimento do conhecimento do professor, nomeadamente sobre discussões coletivas. Com base num modelo sobre práticas e ações a considerar na preparação e condução da discussão coletiva, são analisados casos que apresentam a forma como professores e futuros professores prepararam, conduziram e refletiram sobre a discussão coletiva, em contexto de estudo de aula. Nota biográfica
|
CP 02 – An Innovative Way of Teaching and Assessing Critical Thinking in MathematicsSergiy Klymchuk, Auckland University of Technology, New Zealand Moderador: João Pedro da Ponte, UIDEF, IE, Universidade de Lisboa Quinta-feira, 18 de julho, 9h30m - 10h30m Resumo Fake news, misinformation and conspiracy theories are getting more common in our society. Therefore, abilities to recognise mistakes and think critically are very important nowadays. Including so-called provocative questions in teaching and assessment in mathematics can enhance students' critical thinking skills. Such questions look like typical routine questions but in fact that have a catch – they are deliberately designed to mislead the solver. The intention is to prepare students for real life better by transferring their critical thinking skills outside the classroom. Results of several studies on attitudes of school mathematics teachers’ and university mathematics lecturers towards using provocative mathematics questions in teaching and assessment are presented in the talk. Practical recommendations for teaching practice are also discussed. Nota biográfica
|
XXXIV SIEM - Painel Plenário (2h)
Sessão especialmente organizada para promover uma discussão sobre um tema de atualidade, com vários intervenientes convidados para o efeito. É preparada e conduzida por um moderador convidado pela organização que solicita intervenções dos vários participantes do painel sobre o tema em discussão e em resposta a questões da assistência que em momento próprio é convidada a intervir.
Desafios de sempre na aprendizagem e no ensino da Matemática: Contributos de Leonor SantosModeradora: Ana Paula Canavarro, Universidade de Évora Intervenientes: Paula Teixeira, Projeto MAT 789 Quarta-feira, 17 de julho, 11h30m - 13h00m Resumo Quando nos referimos à aprendizagem e ao ensino da Matemática, uma das ideias que imediatamente surge é a de complexidade, de um contexto de trabalho difícil, onde são múltiplos os problemas a enfrentar, e onde existem desafios que perduram no tempo. Leonor Santos conceptualizou a atividade do professor como uma atividade permanente de resolução de problemas e (e)laborou sobre diversas ideias que constituem desafios de sempre, procurando responder-lhes com propostas efetivas de trabalho que foram além de teoria e se desenvolveram na(s) prática(s). Neste painel, procuramos sistematizar e destacar ideias-chave do seu trabalho em prol da qualidade da aprendizagem e do ensino da Matemática, através de testemunhos de quem trabalhou em diversos contextos profissionais, numa homenagem a esta profissional de valor ímpar cuja obra marcou a evolução dos caminhos da educação matemática em Portugal – e que nos continuará sempre a inspirar. |
XXXIV SIEM - Conferência com discussão (1h)
Pensamento estatístico: a importância decisiva do contextoSusana Carreira, Universidade do Algarve Moderadora: Nádia Ferreira, CIE, ISPA - Instituto Universitário, Portugal Quarta-feira, 17 de julho, 10h00m - 11h00m Resumo A Estatística utiliza formas de pensamento específicas e o desenvolvimento do pensamento estatístico no ensino secundário deve incluir abordagens exploratórias de dados autênticos, em que se detetam padrões e tendências, se identificam modelos e se reconhecem casos excecionais num conjunto de dados. Os contextos devem ser parte integrante da análise e interpretação de dados reais, de tal modo que os alunos consigam compreender e discutir criticamente o mundo em seu redor e a realidade económica, social e cultural em que participam. Trata-se, portanto, de promover e desenvolver o sentido crítico dos alunos, enquanto cidadãos produtores e consumidores de dados. A educação estatística inclui a tomada de consciência de que inúmeros problemas da atualidade são abordados a partir da obtenção e análise de grandes quantidades de dados. Em sintonia com as novas Aprendizagens Essenciais de Matemática A, Matemática B e Matemática dos Cursos Profissionais, do ensino secundário, darei especial atenção à importância do contexto de um problema ou de uma investigação estatística para o desenvolvimento do pensamento estatístico. Nota biográfica
Susana Carreira – Professora Associada da Faculdade de Ciências e Tecnologia da Universidade do Algarve e Professora Associada Convidada do Instituto de Educação da Universidade de Lisboa. É doutorada em Didática da Matemática pela Universidade de Lisboa. Desenvolve investigação em Educação Matemática, nomeadamente nas seguintes áreas: modelação e aplicações no ensino e aprendizagem da matemática; tecnologias na educação matemática, resolução de problemas, criatividade matemática, aspetos afetivos na educação matemática. É autora de livros e artigos científicos em revistas nacionais e internacionais. Tem orientado estudantes de mestrado e de doutoramento, em Portugal e no Brasil. Fez parte da equipa que elaborou as novas Aprendizagens Essenciais de Matemática para o ensino secundário, homologadas em 2023. |
XXXIV SIEM - Simpósios de Comunicações e Pósteres

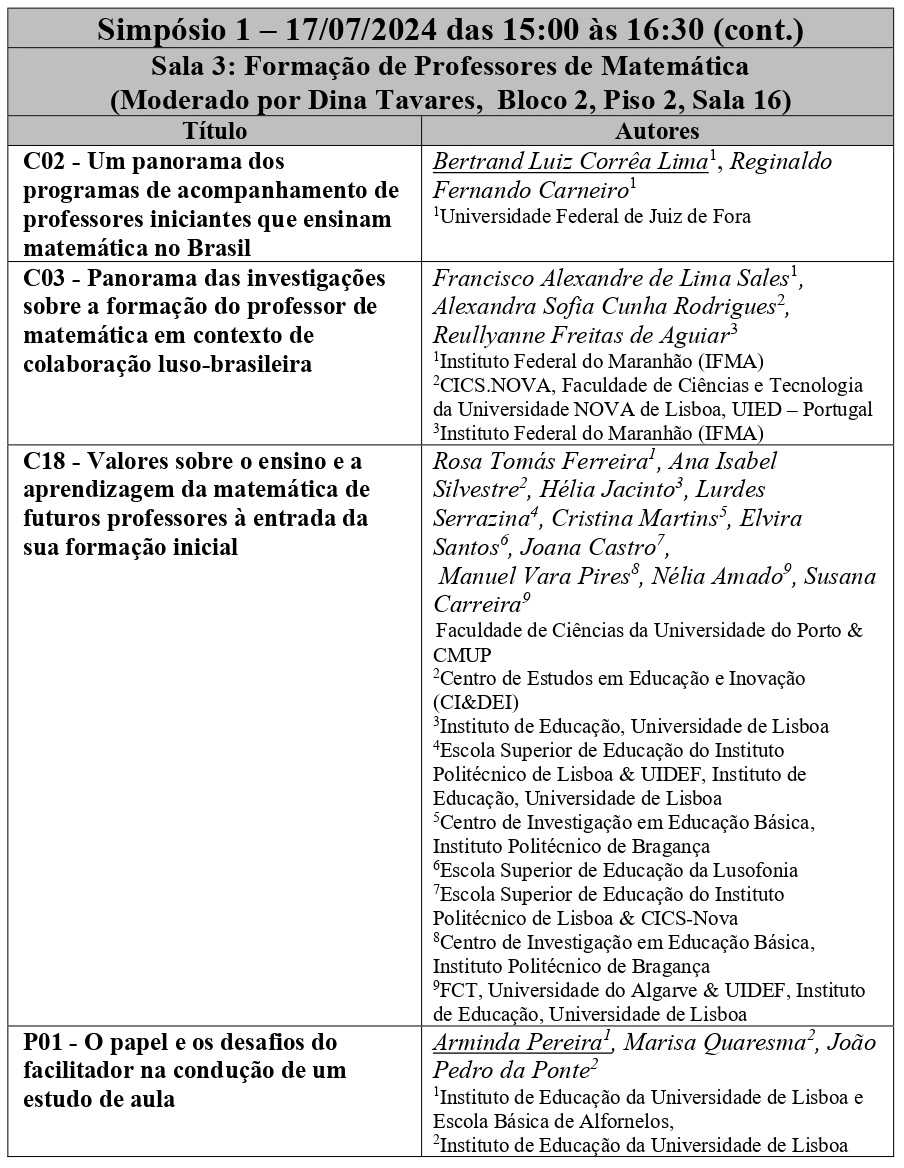
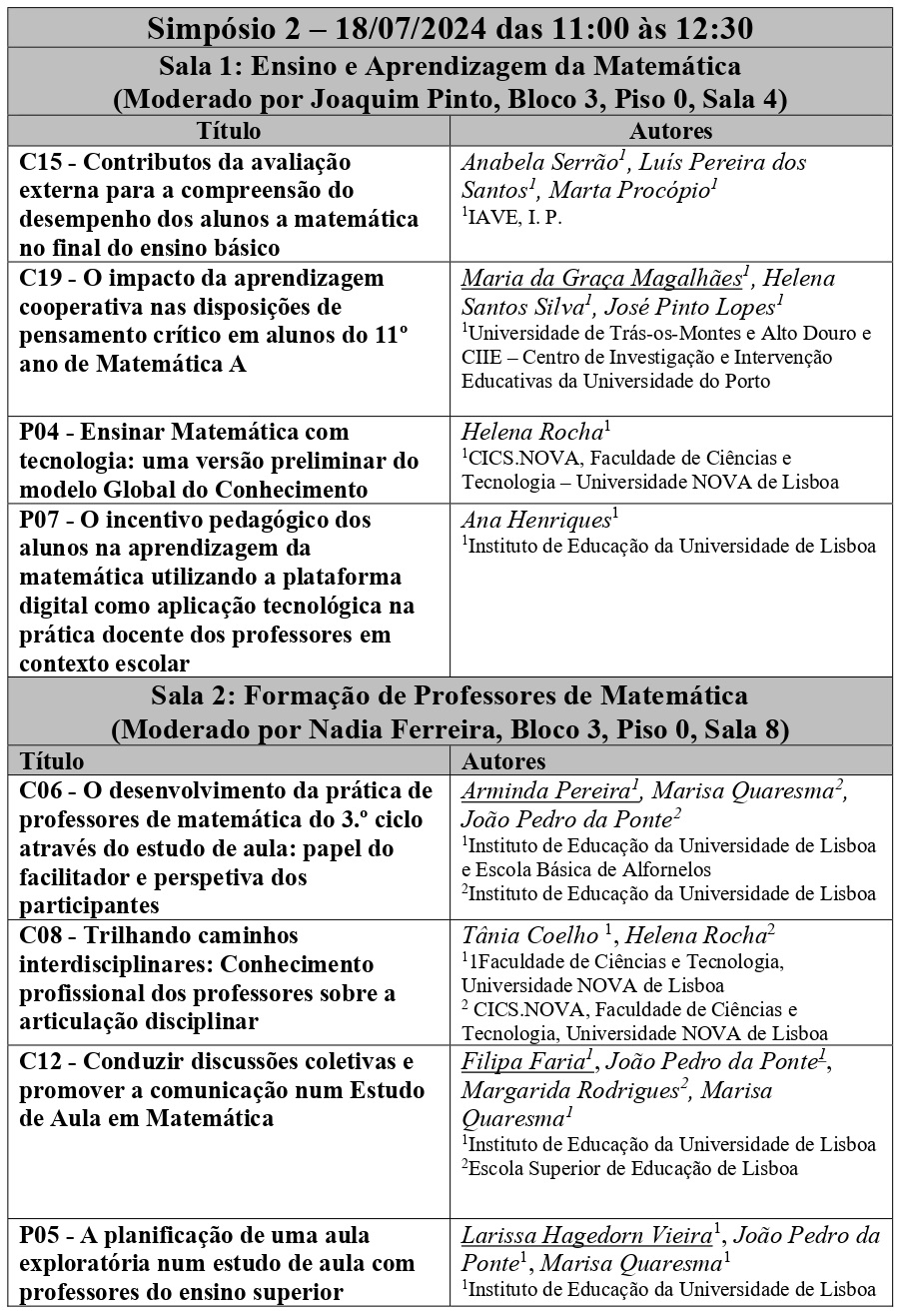
RESUMOS
_page-0001.jpg)
_page-0002.jpg)
_page-0003.jpg)
_page-0004.jpg)
_page-0005.jpg)
_page-0006.jpg)
_page-0007.jpg)
_page-0008.jpg)
_page-0009.jpg)
_page-0010.jpg)
ABSTRACTS
_page-0001.jpg)
_page-0002.jpg)
_page-0003.jpg)
_page-0004.jpg)
_page-0005b.jpg)
_page-0006.jpg)
_page-0007.jpg)
_page-0008.jpg)
_page-0009.jpg)
_page-0010.jpg)
XXXIV SIEM - ESPAÇO GTI
Investigação e Aprendizagens Essenciais do Ensino SecundárioModerador: Cláudia Maria Canha Nunes Johnen Torres, Coordenadora Projeto #EstudoEmCasa Apoia e docente do AE D. Dinis Participantes: António Domingos, Faculdade de Ciências da Universidade Nova de Lisboa Quarta-feira, 17 de julho, 17h00m - 18h00m Resumo O espaço GTI constituiu-se como um espaço informal de troca de ideias sobre um tema da atualidade para a investigação em Educação Matemática. Este ano propomos dar sequência à reflexão iniciada no ano anterior e conversar com membros das equipas das Aprendizagens Essenciais (AE) do Ensino Básico e do Ensino Secundário sobre o papel desempenhado pela investigação no desenvolvimento e implementação das mesmas. Em concreto debateremos como a investigação suporta a organização da formação de professores e o desenvolvimento de materiais curriculares de apoio às AE, para além da definição das próprias AE. Notas biográficas
António Domingos – Licenciado em Matemática e Desenho, Mestre em Ciências da Educação e Doutor e na mesma área, com a especialidade de Teoria e Desenvolvimento Curricular, ambas as especializações realizadas na Faculdade de Ciências e Tecnologia da UNL. Professor Auxiliar no Departamento de Ciências Sociais Aplicadas da FCT NOVA, lecionando no Mestrado em Ensino da Matemática, no Mestrado em Educação e o Programa Doutoral em Educação NOVA-ISPA. É investigador do CICS NOVA e coordenador da UIED, onde tem participado em vários projetos de investigação financiados. É sócio de várias associações profissionais tendo integrado a Direção da APM e sendo atualmente membro da Direção da SPIEM. Os principais interesses de investigação prendem-se com as questões relacionadas com o Ensino e Aprendizagem da Matemática, a integração das Tecnologias no Ensino e Aprendizagem, o Desenvolvimento Curricular em Matemática e aspetos relacionados com a História do Ensino da Matemática.
Susana Carreira – Professora Associada da Faculdade de Ciências e Tecnologia da Universidade do Algarve e Professora Associada Convidada do Instituto de Educação da Universidade de Lisboa. É doutorada em Didática da Matemática pela Universidade de Lisboa. Desenvolve investigação em Educação Matemática, nomeadamente nas seguintes áreas: modelação e aplicações no ensino e aprendizagem da matemática; tecnologias na educação matemática, resolução de problemas, criatividade matemática, aspetos afetivos na educação matemática. É autora de livros e artigos científicos em revistas nacionais e internacionais. Tem orientado estudantes de mestrado e de doutoramento, em Portugal e no Brasil. Fez parte da equipa que elaborou as novas Aprendizagens Essenciais de Matemática para o ensino secundário, homologadas em 2023. |
Espetáculo: A Peste
ESPETÁCULO: A PESTE
Segunda-feira, 15 de julho, 21h30m - 22h30m
Local: Auditório da Escola Secundária Rafael Bordalo Pinheiro
LOTAÇÃO: 200 PESSOAS
Grupo de Teatro "Os Bordalitos"
Título do Espetáculo: A Peste
Dramaturgia: Criação coletiva baseada em “Estado de Sítio” de Albert Camus
Direção: Amábile Maria
Elenco:
Ana Silva
Carmem Stroo Cloeck
Charlie
Constança Fonseca
Cléo
Diogo Jesus
Fernanda Monteiro
Letícia Pinheiro
Maria Lima
Mathis Audigane
Matilde Lima
Sal S. Nicolau
Sinopse:
"Estado de Sítio", de Albert Camus, é uma peça teatral que examina a natureza do poder, da liberdade e da resistência face à opressão. Retrata um regime totalitário que controla seus cidadãos através do medo e da subjugação. Quando a cidade de Caldas da Rainha é colocada como cenário, a história ganha uma dimensão atual e passa a questionar: quais são os absurdos do mundo de hoje? O que aconteceria se o absurdo se transformasse em lei? Enquanto os habitantes lutam para preservar sua liberdade, a peça explora as tensões do autoritarismo e da democracia."
Visitas guiadas
VISITAS GUIADAS ÀS CALDAS DA RAINHA
Visitas organizadas pelo Município das Caldas da Rainha - Unidade de Turismo
Terça-feira, 16 de julho, 18h30m - 19h30m
Para cada uma das tês visitas, foram selecionados 35 participantes, de acordo com a ordem de inscrição no ProfMat/SIEM e atendendo às preferências indicadas no formulário de inscrição. As listas de participantes selecionados serão afixadas no Centro Cultural e de Congressos.
Local de partida: Centro Cultural e de Congressos (Praça da Animação)
Visita 1 - História e património termal das Caldas da Rainha
Visita 1 - Visita ao complexo termal, a zona fundacional da cidade. Os visitantes terão oportunidade de compreender a história da cidade, com uma visita ao Hospital Termal.
Visita 2 - Percurso das águas termais das Caldas da Rainha
Visita 2 - Contextualização histórica e científica do percurso das águas termais. Esta visita terá lugar na Mata Rainha Dona Leonor, erguida para proteger as nascentes das águas termais.
Visita 3 - Parque D. Carlos I, História e biodiversidade
Visita 3 - Visita ao Parque D. Carlos I, parque romântico do século XIX, localizado no coração da cidade. Através desta visita, irá saber um pouco mais da sua história e origens, assim como a biodiversidade que o compõe e enriquece.
Prazos
PROFMAT 2024
| Inscrição ProfMat 1.º prazo (ADIAMENTO) | até 14 de junho |
| Submissões de Sessão Práticas e/ou Comunicações | até 19 de maio |
| Notificação de aceitação | até 5 de junho |
| Inscrição ProfMat 2.º prazo | de 15 a 30 de junho |
| Inscrição ProfMat 3.º prazo | até 07 de julho |
SIEM 2024
| Inscrição ProfMat 1.º prazo (ADIAMENTO) | até 14 de junho |
| Submissões de Comunicações e/ou Pósteres | até 19 de maio |
| Notificação de aceitação e indicações de revisão | até 31 de maio |
| Submissão da versão final revista para publicação em atas | até 17 de junho |
| Inscrição sem multa para autores Comunicações/Pósteres | até 20 de junho |
| Inscrição SIEM 2.º prazo | de 15 a 30 de junho |
| Inscrição SIEM 3.º prazo | até 07 de julho |
Preços
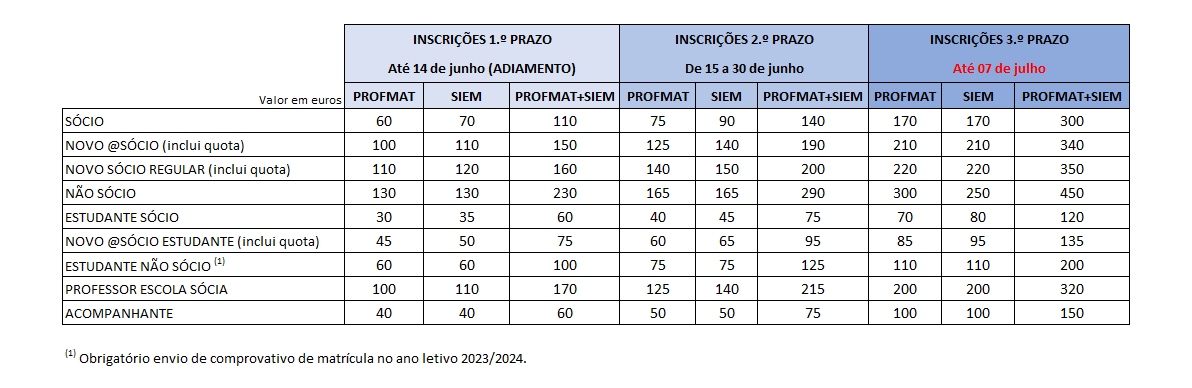
Na tabela acima, encontram-se os preços de inscrição para estes encontros, por prazo e situação do participante.
Data limite de devoluções
Até 23 de junho, as desistências são reembolsadas em 50% do valor pago. Após esta data, não há lugar a devoluções.
Inscrição
A inscrição no encontro ProfMat 2024 e/ou SIEM 2024 requer o preenchimento de um formulário de inscrição.
Após completar a sua inscrição, terminando com a submissão desse formulário, deve efetuar a transferência bancária referente ao valor total da sua inscrição (total da inscrição, incluindo jantar e/ou almoços caso selecione estas opções) para a conta da APM com o IBAN PT50003503250000664993010 e enviar comprovativo para centroformacao@apm.pt (logo após efetuar a sua inscrição).
No descritivo da transferência bancária, no caso dos associados da APM deve constar o número de sócio e/ou primeiro e último nome, no caso dos não sócios o primeiro e último nome.
A inscrição só fica concluída após o envio do comprovativo de pagamento.
Para se inscrever no ProfMat e/ou SIEM, clique no botão abaixo:
| Inscrição |
Apoios
Parceiros Institucionais (na organização)
 |
 |
 |
 |
Parceiros - Agrupamentos de Escolas
 |
 |
Parceiros - Tecnologia na Educação Matemática
 |
 |
 |
 |
 |
Parceiros - Editoras na Educação Matemática
 |
 |
 |
 |
Parceiros - Ofertas a participantes
 |
 |
 |
 |
Parceiros - Alojamento
Para mais informações, consulte o separador "PofMat 2024" > "Alojamentos com protocolo".
 |
 |
 |
 |
 |
 |
 |











 Maria Clara Martins
Maria Clara Martins























 Nicole Duarte é Doutora em Educação, na especialidade de Didática da Matemática, pelo Instituto de Educação da Universidade de Lisboa e Professora Adjunta Convidada na Escola Superior de Educação e Ciências Sociais do Instituto Politécnico de Leiria. É investigadora integrada no Centro de Estudos em Educação e Inovação (CI&DEI) e tem investigado sobre o estudo de aula na formação inicial de professores, com foco no desenvolvimento do seu conhecimento didático, e em particular no que respeita à discussão coletiva. Integra equipas de investigação no âmbito dos projetos Introduzindo o estudo de aula na formação inicial de professores e O pensamento computacional na formação inicial de professores dos primeiros anos.
Nicole Duarte é Doutora em Educação, na especialidade de Didática da Matemática, pelo Instituto de Educação da Universidade de Lisboa e Professora Adjunta Convidada na Escola Superior de Educação e Ciências Sociais do Instituto Politécnico de Leiria. É investigadora integrada no Centro de Estudos em Educação e Inovação (CI&DEI) e tem investigado sobre o estudo de aula na formação inicial de professores, com foco no desenvolvimento do seu conhecimento didático, e em particular no que respeita à discussão coletiva. Integra equipas de investigação no âmbito dos projetos Introduzindo o estudo de aula na formação inicial de professores e O pensamento computacional na formação inicial de professores dos primeiros anos. Dr Sergiy Klymchuk is an Associate Professor of mathematics and Founding Director of the STEM Tertiary Education Centre at the Auckland University of Technology, New Zealand. He has 43 years' experience in teaching university mathematics in different countries. His PhD was in differential equations and current research interests are in mathematics education. He authored or co-authored more than 250 publications including the Counterexamples in Calculus book that received an Outstanding Academic Title Award from the Choice magazine of the American Library Association in 2010; Paradoxes and Sophisms in Calculus book that made the cover of the 2014 Publications Catalogue of the Mathematical Association of America; and the internationally acclaimed book on popular mathematics Money Puzzles: On Critical Thinking and Financial Literacy that has been published in 9 countries. He is a Fellow of the Institute of Mathematics and its Applications based in the UK, a member of the Royal Society of New Zealand and several international organisations on mathematics education.
Dr Sergiy Klymchuk is an Associate Professor of mathematics and Founding Director of the STEM Tertiary Education Centre at the Auckland University of Technology, New Zealand. He has 43 years' experience in teaching university mathematics in different countries. His PhD was in differential equations and current research interests are in mathematics education. He authored or co-authored more than 250 publications including the Counterexamples in Calculus book that received an Outstanding Academic Title Award from the Choice magazine of the American Library Association in 2010; Paradoxes and Sophisms in Calculus book that made the cover of the 2014 Publications Catalogue of the Mathematical Association of America; and the internationally acclaimed book on popular mathematics Money Puzzles: On Critical Thinking and Financial Literacy that has been published in 9 countries. He is a Fellow of the Institute of Mathematics and its Applications based in the UK, a member of the Royal Society of New Zealand and several international organisations on mathematics education. Cláudia Maria Canha Nunes Johnen Torres – Coordenadora do Projeto #EstudoEmCasa Apoia desde 2021 e professora de Quadro do Agrupamento de Escolas D. Dinis em Lisboa é Doutorada em Educação, na Área de especialização da Didática da Matemática, pela Instituto de Educação da Universidade de Lisboa, com a tese A liderança e a gestão curricular no contexto de um grupo de professores de matemática (2014), e professora de Matemática do 3.º ciclo do ensino básico e ensino secundário há 28 anos. Participou em diversos projetos de investigação nacionais (Membro da Equipa de Projeto de avaliação de Manuais escolares, Membro da Equipa de Projeto Mais Sucesso Escolar, tipologia híbrida; e, mais recentemente, o CRIarte - educação inclusiva e Ecossistemas de Aprendizagem e Bem-estar) e internacionais (PDTR – Professional Development of Teachers’ Researchers e LPS – Learning from Students perspective).
Cláudia Maria Canha Nunes Johnen Torres – Coordenadora do Projeto #EstudoEmCasa Apoia desde 2021 e professora de Quadro do Agrupamento de Escolas D. Dinis em Lisboa é Doutorada em Educação, na Área de especialização da Didática da Matemática, pela Instituto de Educação da Universidade de Lisboa, com a tese A liderança e a gestão curricular no contexto de um grupo de professores de matemática (2014), e professora de Matemática do 3.º ciclo do ensino básico e ensino secundário há 28 anos. Participou em diversos projetos de investigação nacionais (Membro da Equipa de Projeto de avaliação de Manuais escolares, Membro da Equipa de Projeto Mais Sucesso Escolar, tipologia híbrida; e, mais recentemente, o CRIarte - educação inclusiva e Ecossistemas de Aprendizagem e Bem-estar) e internacionais (PDTR – Professional Development of Teachers’ Researchers e LPS – Learning from Students perspective). 


